Kubovčík, M.: Kužeľosečky
4. Kužeľosečka ako rovinný rez rotačnej kužeľovej plochy
4.3. Dôkaz vety pre hyperbolu
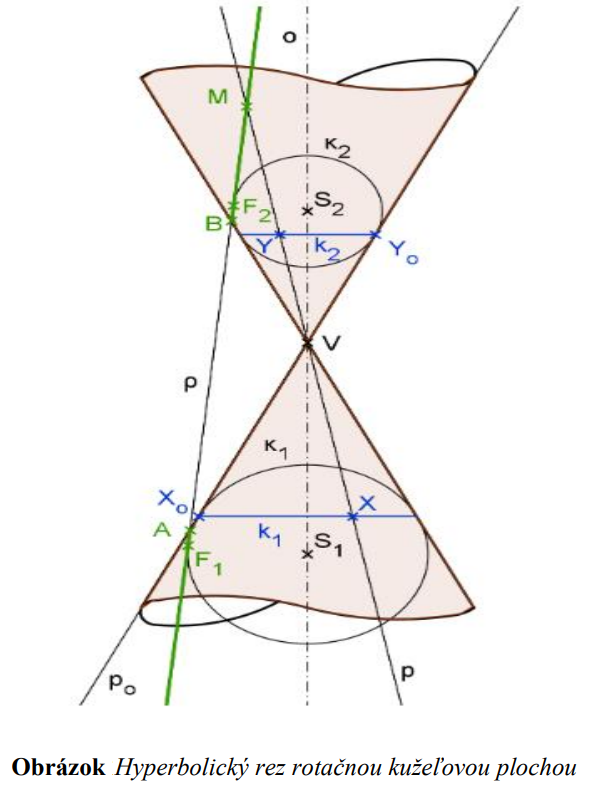
Nech je daná rotačná kužeľová plocha  a rovinný rez
a rovinný rez  rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
Ak chceme dokázať, že prienik rovinného rezu a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je hyperbola, tak nám stačí ukázať,
je hyperbola, tak nám stačí ukázať,
že body tohto prieniku majú konštantný rozdiel vzdialeností od dvoch pevných bodov (ohniská).
(ohniská).
Do rotačnej kužeľovej plochy vpíšeme guľové plochy
vpíšeme guľové plochy 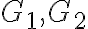 (dotýkajúce sa kužeľovej plochy pozdĺž kružníc
(dotýkajúce sa kužeľovej plochy pozdĺž kružníc 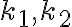 ) tak,
) tak,
aby rovinný rez bol ich dotyková rovina. Body dotyku označíme
bol ich dotyková rovina. Body dotyku označíme  .
.
Zvolíme si ľubovoľný bod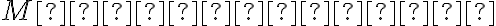 . Budeme viesť povrchovú priamku rotačnej kužeľovej plochy
. Budeme viesť povrchovú priamku rotačnej kužeľovej plochy  prechádzajúcu týmto bodom.
prechádzajúcu týmto bodom.
Označme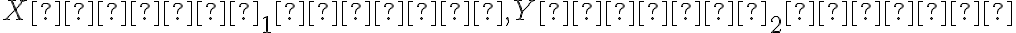 . Platí:
. Platí:
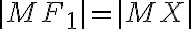 ,
,
pretože priamky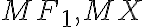 sú dotyčnice guľovej plochy
sú dotyčnice guľovej plochy 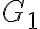 a zároveň body
a zároveň body 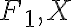 na tejto guľovej ploche ležia. Obdobne platí:
na tejto guľovej ploche ležia. Obdobne platí:
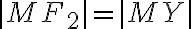 .
.
Dostávame, že:
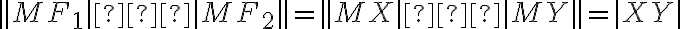 .
.
Takto sme dostali, že všetky také body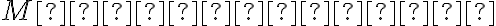 sú vzdialené od dvoch pevných bodov
sú vzdialené od dvoch pevných bodov  o konštantný rozdiel vzdialeností.
o konštantný rozdiel vzdialeností.
Takúto množinu bodov danej vlastnosti nazývame hyperbola.
 a rovinný rez
a rovinný rez  rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
Ak chceme dokázať, že prienik rovinného rezu
 a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je hyperbola, tak nám stačí ukázať,
je hyperbola, tak nám stačí ukázať,
že body tohto prieniku majú konštantný rozdiel vzdialeností od dvoch pevných bodov
 (ohniská).
(ohniská).
Do rotačnej kužeľovej plochy
 vpíšeme guľové plochy
vpíšeme guľové plochy 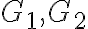 (dotýkajúce sa kužeľovej plochy pozdĺž kružníc
(dotýkajúce sa kužeľovej plochy pozdĺž kružníc 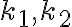 ) tak,
) tak,
aby rovinný rez
 bol ich dotyková rovina. Body dotyku označíme
bol ich dotyková rovina. Body dotyku označíme  .
.
Zvolíme si ľubovoľný bod
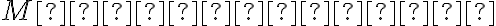 . Budeme viesť povrchovú priamku rotačnej kužeľovej plochy
. Budeme viesť povrchovú priamku rotačnej kužeľovej plochy  prechádzajúcu týmto bodom.
prechádzajúcu týmto bodom.
Označme
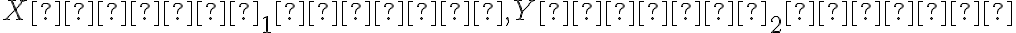 . Platí:
. Platí:
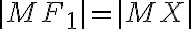 ,
,
pretože priamky
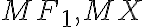 sú dotyčnice guľovej plochy
sú dotyčnice guľovej plochy 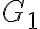 a zároveň body
a zároveň body 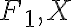 na tejto guľovej ploche ležia. Obdobne platí:
na tejto guľovej ploche ležia. Obdobne platí:
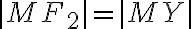 .
.
Dostávame, že:
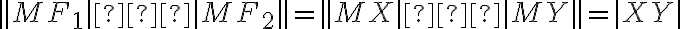 .
.
Takto sme dostali, že všetky také body
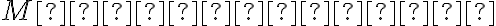 sú vzdialené od dvoch pevných bodov
sú vzdialené od dvoch pevných bodov  o konštantný rozdiel vzdialeností.
o konštantný rozdiel vzdialeností.
Takúto množinu bodov danej vlastnosti nazývame hyperbola.

