Vektorový a afinný priestor
Afinný n-rozmerný priestor
Veta o súradniciach
V predchádzajúcej kapitole sme uviedli:
Súradnice bodu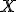 afinného priestoru
afinného priestoru 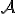 vzhľadom na danú afinnú sústavu súradníc sú súradnice jeho polohového
vektora
vzhľadom na danú afinnú sústavu súradníc sú súradnice jeho polohového
vektora 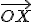 vzhľadom na bázu súradnicových vektorov. Teda platí
vzhľadom na bázu súradnicových vektorov. Teda platí
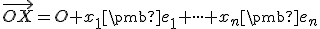 .
.
Súradnice bodu
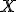 afinného priestoru
afinného priestoru 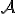 vzhľadom na danú afinnú sústavu súradníc sú súradnice jeho polohového
vektora
vzhľadom na danú afinnú sústavu súradníc sú súradnice jeho polohového
vektora 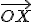 vzhľadom na bázu súradnicových vektorov. Teda platí
vzhľadom na bázu súradnicových vektorov. Teda platí
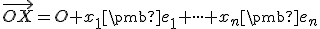 .
.
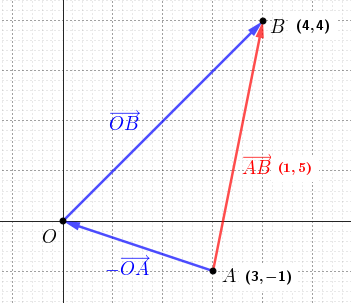
Po zavedení súradnej sústavy môžeme nielen vektory ale aj body "sčitovať". Pravidlá, ktoré musíme pritom dodržiavať stanovuje tzv. základná
veta o súradniciach, ktorú poznáme z lineárnej algebry.
Dôkaz.
- Zrejme z vlastnosti (AP1) afinného priestoru vyplýva, že
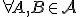 a pre začiatok súradnej sústavy
a pre začiatok súradnej sústavy 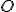 bude platiť
bude platiť 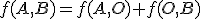 tj.
tj. 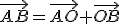 odkiaľ s využitím "Tvrdenie
(operácie s bodmi), odseky b), e)" dostaneme
odkiaľ s využitím "Tvrdenie
(operácie s bodmi), odseky b), e)" dostaneme
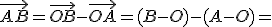
po úprave
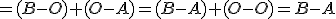 .
.
Z definície sčítania (rozdielu) vektorov v báze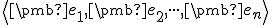 dostaneme
dostaneme
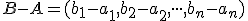
- Z vlastnosti (AP2') afinného priestoru vyplýva, že
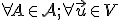 existuje práve jeden bod
existuje práve jeden bod
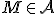 taký, že
taký, že 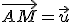 . Pre polohové vektory platí
. Pre polohové vektory platí
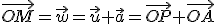 .
.
Z vlastnosti sčítania vektorov dostaneme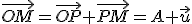 .
.
Po úprave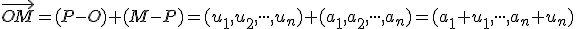 .
.
Zmena repéru
Pri závádzaní lineárnej súradnicovej sústavy sa v definícii nekládla požiadavka ortonormálnosti na repér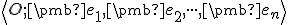 afinného priestoru
afinného priestoru 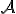 . To znamená, že súradnice
nejakého bodu
. To znamená, že súradnice
nejakého bodu 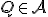 môžeme vyjadriť aj vzhľadom na ľubovoľný iný repér. Ako určiť súradnice bodu pri zmene repéru popisuje nasledujúci príklad.
môžeme vyjadriť aj vzhľadom na ľubovoľný iný repér. Ako určiť súradnice bodu pri zmene repéru popisuje nasledujúci príklad.
Pri závádzaní lineárnej súradnicovej sústavy sa v definícii nekládla požiadavka ortonormálnosti na repér
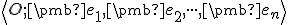 afinného priestoru
afinného priestoru 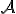 . To znamená, že súradnice
nejakého bodu
. To znamená, že súradnice
nejakého bodu 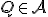 môžeme vyjadriť aj vzhľadom na ľubovoľný iný repér. Ako určiť súradnice bodu pri zmene repéru popisuje nasledujúci príklad.
môžeme vyjadriť aj vzhľadom na ľubovoľný iný repér. Ako určiť súradnice bodu pri zmene repéru popisuje nasledujúci príklad.
Príklad.
Riešenie.
- Zrejme
![\small R = [1,-2,1]+(-2).(1, 1, 2) + 1(-3, 2, 1) + 2.(-2, 1, 0) = (-8, 0, -2) \small R = [1,-2,1]+(-2).(1, 1, 2) + 1(-3, 2, 1) + 2.(-2, 1, 0) = (-8, 0, -2)](https://lms.umb.sk/filter/tex/pix.php/f016c1c3a707de12152526046bbb004c.png) .
.
Toto sú súradnice bodu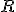 vzhľadom k ortonormálnemu repéru - kanonické súradnice. Je dôležité dodržať poradie prvkov repéru
vzhľadom k ortonormálnemu repéru - kanonické súradnice. Je dôležité dodržať poradie prvkov repéru  . Urobte geometrickú interpretáciu.
. Urobte geometrickú interpretáciu. - Určiť súradnice vzhľadom k repéru
 znamená bod
znamená bod  vyjadriť ako lineárnu kombináciu prvkov repéru
vyjadriť ako lineárnu kombináciu prvkov repéru  .
Opäť treba dať pozor na poradie prvkov bázy. Musíme nájsť
.
Opäť treba dať pozor na poradie prvkov bázy. Musíme nájsť 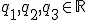 , pre ktoré platí:
, pre ktoré platí:
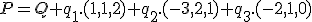 resp.
resp.
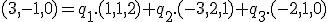 .
.
Úlohu môžeme riešiť ako sústavu rovníc (vyriešte úlohu týmto spôsobom).
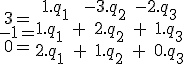
Poslednú rovnosť môžeme vyjadriť v maticovom tvare (vektory repéru zapisujeme do stĺpcov!):
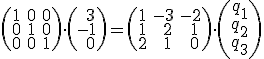 Riešením je bod
Riešením je bod 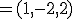 .
.
Riešenie.
- Algebraické riešenie: Dosaďte do výrazu
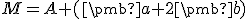 hodnoty za
hodnoty za 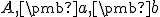 a dostanete súradnice
a dostanete súradnice ![[1,5,-2] [1,5,-2]](https://lms.umb.sk/filter/tex/pix.php/ecdc55665c1fccb7a9d931f03454e170.png) .
. - Grafické riešenie: Aktivujte si repér
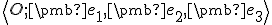 v GeoGebre
Tu.
Do vstupného poľa postupne zadajte
v GeoGebre
Tu.
Do vstupného poľa postupne zadajte 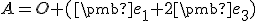 ,
, 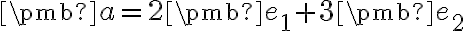 ,
, 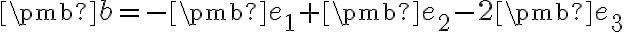 a
a 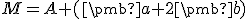 . Porovnajte výsledok.
. Porovnajte výsledok.
![\small A=[a_1,a_2, \cdot \cdot \cdot , a_n], B=[b_1,b_2, \cdot \cdot \cdot , b_n] \in \mathcal A \small A=[a_1,a_2, \cdot \cdot \cdot , a_n], B=[b_1,b_2, \cdot \cdot \cdot , b_n] \in \mathcal A](https://lms.umb.sk/filter/tex/pix.php/261b65e9911f1b06ec0962250640e3ce.png)
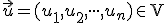
![\small A+\vec u=[a_1+u_1,a_2+u_2, \cdot \cdot \cdot , a_n+u_n] \small A+\vec u=[a_1+u_1,a_2+u_2, \cdot \cdot \cdot , a_n+u_n]](https://lms.umb.sk/filter/tex/pix.php/d996c24c4f0167368e127f25e2dca5fa.png)
![\small S= \left\langle {Q[1,-2,1],\vec a (1, 1, 2),\;\vec b(-3, 2, 1),\;\vec c (-2, 1, 0) }\right\rangle \small S= \left\langle {Q[1,-2,1],\vec a (1, 1, 2),\;\vec b(-3, 2, 1),\;\vec c (-2, 1, 0) }\right\rangle](https://lms.umb.sk/filter/tex/pix.php/2a7471cea093344d706c58d3a02f2507.png)
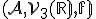
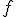
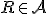
![\small [-2, 1, 2] \small [-2, 1, 2]](https://lms.umb.sk/filter/tex/pix.php/dc9121ac8fc58ff90745e1f3d6118867.png)
![\small P = [4,-3,1] \small P = [4,-3,1]](https://lms.umb.sk/filter/tex/pix.php/fad406c20a268ba80726f0debea151a3.png)
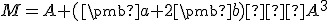
![\small [O;\pmb {e_1} ,\pmb {e_2} ,\pmb {e_3} ] \small [O;\pmb {e_1} ,\pmb {e_2} ,\pmb {e_3} ]](https://lms.umb.sk/filter/tex/pix.php/44d228191e592295cf515854200bd36d.png)
