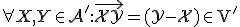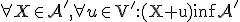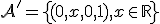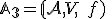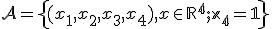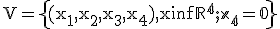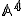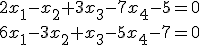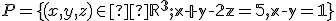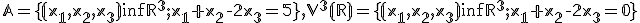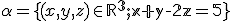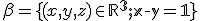Vektorový a afinný priestor
Afinný n-rozmerný priestor
Afinný podpriestor
Zvoľme si v afinnom priestore 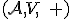 jeden pevný bod
jeden pevný bod 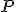 a nejaké zameranie
a nejaké zameranie 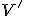 , ktoré je podmnožinou vektorového zamerania
, ktoré je podmnožinou vektorového zamerania 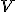 . Dostaneme podmnožinu bodov afinného priestoru, ktorá bude spĺňať axiómy afinného priestoru. Takouto množinou je napríklad priamka v euklidovskej rovine alebo rovina v euklidovskom priestore.
. Dostaneme podmnožinu bodov afinného priestoru, ktorá bude spĺňať axiómy afinného priestoru. Takouto množinou je napríklad priamka v euklidovskej rovine alebo rovina v euklidovskom priestore.
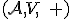 jeden pevný bod
jeden pevný bod 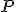 a nejaké zameranie
a nejaké zameranie 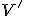 , ktoré je podmnožinou vektorového zamerania
, ktoré je podmnožinou vektorového zamerania 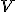 . Dostaneme podmnožinu bodov afinného priestoru, ktorá bude spĺňať axiómy afinného priestoru. Takouto množinou je napríklad priamka v euklidovskej rovine alebo rovina v euklidovskom priestore.
. Dostaneme podmnožinu bodov afinného priestoru, ktorá bude spĺňať axiómy afinného priestoru. Takouto množinou je napríklad priamka v euklidovskej rovine alebo rovina v euklidovskom priestore.
Definícia.
Nech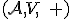 je afinný priestor nad poľom
je afinný priestor nad poľom 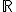 . Neprázdnu podmnožinu
. Neprázdnu podmnožinu 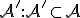 nazývame afinný podpriestor resp. lineárna varieta afinného priestoru
nazývame afinný podpriestor resp. lineárna varieta afinného priestoru 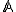 ,
ak existuje vektorový podpriestor
,
ak existuje vektorový podpriestor 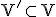 , pričom platí
, pričom platí
Nech
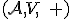 je afinný priestor nad poľom
je afinný priestor nad poľom 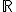 . Neprázdnu podmnožinu
. Neprázdnu podmnožinu 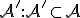 nazývame afinný podpriestor resp. lineárna varieta afinného priestoru
nazývame afinný podpriestor resp. lineárna varieta afinného priestoru 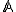 ,
ak existuje vektorový podpriestor
,
ak existuje vektorový podpriestor 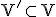 , pričom platí
, pričom platí
Tvrdenie.
Nech![\small X= [x_1, x_2, \cdot \cdot \cdot x_n] \small X= [x_1, x_2, \cdot \cdot \cdot x_n]](https://lms.umb.sk/filter/tex/pix.php/849e663d14ddce160818d00568aeb6ba.png) je ľubovoľný bod z afinného priestoru
je ľubovoľný bod z afinného priestoru 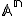 . Potom bod
. Potom bod 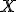 leží v podpriestore
leží v podpriestore 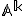 , práve vtedy, keď platí rovnosť
, práve vtedy, keď platí rovnosť
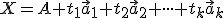 ,
,
kde![\small A= [a_1, a_2, \cdot \cdot \cdot a_n] \in \mathcal A^k \small A= [a_1, a_2, \cdot \cdot \cdot a_n] \in \mathcal A^k](https://lms.umb.sk/filter/tex/pix.php/6842e3db0adab2c2a859a2aef4c471cd.png) ;
; 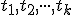 sú reálne čísla a
sú reálne čísla a 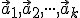 je
je 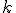 lineárne nezávislých vektorov
podpriestoru
lineárne nezávislých vektorov
podpriestoru 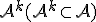 . Uvedená rovnosť sa nazýva parametrické vyjadrenie podpriestoru
. Uvedená rovnosť sa nazýva parametrické vyjadrenie podpriestoru 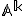 . Čísla
. Čísla 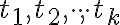 sa nazývajú parametre bodu
sa nazývajú parametre bodu 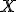 .
.
Nech
![\small X= [x_1, x_2, \cdot \cdot \cdot x_n] \small X= [x_1, x_2, \cdot \cdot \cdot x_n]](https://lms.umb.sk/filter/tex/pix.php/849e663d14ddce160818d00568aeb6ba.png) je ľubovoľný bod z afinného priestoru
je ľubovoľný bod z afinného priestoru 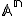 . Potom bod
. Potom bod 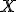 leží v podpriestore
leží v podpriestore 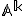 , práve vtedy, keď platí rovnosť
, práve vtedy, keď platí rovnosť
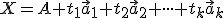 ,
,
kde
![\small A= [a_1, a_2, \cdot \cdot \cdot a_n] \in \mathcal A^k \small A= [a_1, a_2, \cdot \cdot \cdot a_n] \in \mathcal A^k](https://lms.umb.sk/filter/tex/pix.php/6842e3db0adab2c2a859a2aef4c471cd.png) ;
; 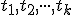 sú reálne čísla a
sú reálne čísla a 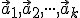 je
je 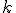 lineárne nezávislých vektorov
podpriestoru
lineárne nezávislých vektorov
podpriestoru 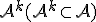 . Uvedená rovnosť sa nazýva parametrické vyjadrenie podpriestoru
. Uvedená rovnosť sa nazýva parametrické vyjadrenie podpriestoru 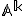 . Čísla
. Čísla 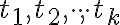 sa nazývajú parametre bodu
sa nazývajú parametre bodu 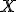 .
.
Poznámky.
Pre rovnosť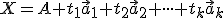 sa tradične používa nie úplne presný názov parametrické rovnice podpriestoru. Parametrické rovnice podpriestoru
sa tradične používa nie úplne presný názov parametrické rovnice podpriestoru. Parametrické rovnice podpriestoru 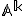 majú známy tvar
majú známy tvar
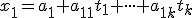
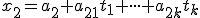
...
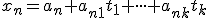 ,
,
kde![\small X= [x_1, x_2, \cdot \cdot \cdot x_n] \small X= [x_1, x_2, \cdot \cdot \cdot x_n]](https://lms.umb.sk/filter/tex/pix.php/849e663d14ddce160818d00568aeb6ba.png) sú súradnice bodu
sú súradnice bodu 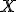 a
a 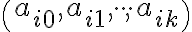 sú súradnice vektora
sú súradnice vektora 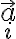 v
kanonickej báze
v
kanonickej báze 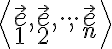 . Túto sústavu rovníc môžeme zapísať pomocou matíc. Maticový tvar parametrických rovníc vyzerá takto
. Túto sústavu rovníc môžeme zapísať pomocou matíc. Maticový tvar parametrických rovníc vyzerá takto
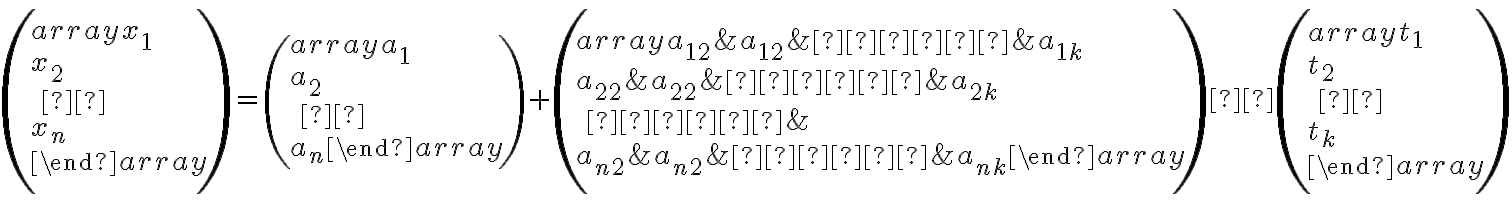
Maticu sústavy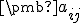 z predchádzajúceho vyjadrenia nazývame matica prechodu od afinnej súradnicovej sústavy
z predchádzajúceho vyjadrenia nazývame matica prechodu od afinnej súradnicovej sústavy
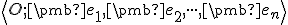 do sústavy
do sústavy
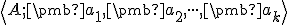 .
.
Pre rovnosť
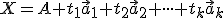 sa tradične používa nie úplne presný názov parametrické rovnice podpriestoru. Parametrické rovnice podpriestoru
sa tradične používa nie úplne presný názov parametrické rovnice podpriestoru. Parametrické rovnice podpriestoru 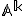 majú známy tvar
majú známy tvar
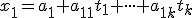
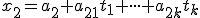
...
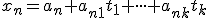 ,
,
kde
![\small X= [x_1, x_2, \cdot \cdot \cdot x_n] \small X= [x_1, x_2, \cdot \cdot \cdot x_n]](https://lms.umb.sk/filter/tex/pix.php/849e663d14ddce160818d00568aeb6ba.png) sú súradnice bodu
sú súradnice bodu 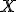 a
a 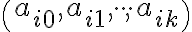 sú súradnice vektora
sú súradnice vektora 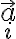 v
kanonickej báze
v
kanonickej báze 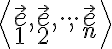 . Túto sústavu rovníc môžeme zapísať pomocou matíc. Maticový tvar parametrických rovníc vyzerá takto
. Túto sústavu rovníc môžeme zapísať pomocou matíc. Maticový tvar parametrických rovníc vyzerá takto
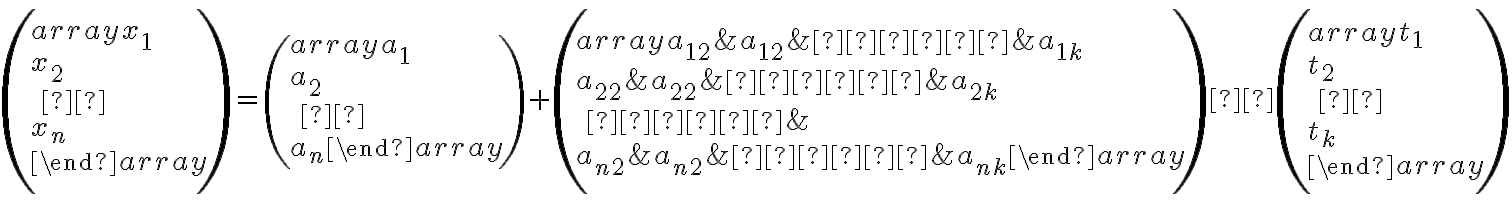
Maticu sústavy
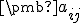 z predchádzajúceho vyjadrenia nazývame matica prechodu od afinnej súradnicovej sústavy
z predchádzajúceho vyjadrenia nazývame matica prechodu od afinnej súradnicovej sústavy
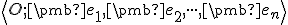 do sústavy
do sústavy
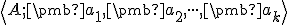 .
.
Príklad 1.
Zistite, či body![\small M = [9, -2, 5], N = [4, 1, 6] \small M = [9, -2, 5], N = [4, 1, 6]](https://lms.umb.sk/filter/tex/pix.php/8a3cde48cba700d2cdcf1f273d3c9937.png) incidujú s podpriestorom (ležia v podpriestore)
incidujú s podpriestorom (ležia v podpriestore) 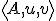 . Dané sú
bod
. Dané sú
bod ![\small A = [1, 3, 2] \small A = [1, 3, 2]](https://lms.umb.sk/filter/tex/pix.php/f7db82372dc4ba7d322d4d064720b97d.png) a vektory
a vektory 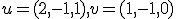 . Nájdite parametrické vyjadrenie tohto podpriestoru. Vytvorte grafickú ilustrácia k tomuto príkladu.
. Nájdite parametrické vyjadrenie tohto podpriestoru. Vytvorte grafickú ilustrácia k tomuto príkladu.
Zistite, či body
![\small M = [9, -2, 5], N = [4, 1, 6] \small M = [9, -2, 5], N = [4, 1, 6]](https://lms.umb.sk/filter/tex/pix.php/8a3cde48cba700d2cdcf1f273d3c9937.png) incidujú s podpriestorom (ležia v podpriestore)
incidujú s podpriestorom (ležia v podpriestore) 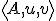 . Dané sú
bod
. Dané sú
bod ![\small A = [1, 3, 2] \small A = [1, 3, 2]](https://lms.umb.sk/filter/tex/pix.php/f7db82372dc4ba7d322d4d064720b97d.png) a vektory
a vektory 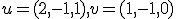 . Nájdite parametrické vyjadrenie tohto podpriestoru. Vytvorte grafickú ilustrácia k tomuto príkladu.
. Nájdite parametrické vyjadrenie tohto podpriestoru. Vytvorte grafickú ilustrácia k tomuto príkladu.
Riešenie.
Hľadáme reálne čísla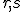 , pre ktoré platí rovnosť (vektorová rovnica má práve jedno riešenie)
, pre ktoré platí rovnosť (vektorová rovnica má práve jedno riešenie)
![\small [9, -2, 5]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0) \small [9, -2, 5]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0)](https://lms.umb.sk/filter/tex/pix.php/987fedb1246681eac4577b8596ffe7df.png) resp.
resp. ![\small [4, 1, 6]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0) \small [4, 1, 6]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0)](https://lms.umb.sk/filter/tex/pix.php/93de6ddda2e4e5ebafc0d01957f5e5fc.png)
Odpoveď: Bod![\small M = [9, -2, 5] \small M = [9, -2, 5]](https://lms.umb.sk/filter/tex/pix.php/4d2415124dd26dc5ad3d4122c173aa75.png) inciduje s daným podpriestorom, riešenie nájdete
Tu. Ukážte, že bod
inciduje s daným podpriestorom, riešenie nájdete
Tu. Ukážte, že bod ![\small N = [4, 1, 6] \small N = [4, 1, 6]](https://lms.umb.sk/filter/tex/pix.php/f2bd7784e5e4385754858ca3d595e26d.png) neleží v danom podpriestore.
neleží v danom podpriestore.
Hľadáme reálne čísla
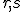 , pre ktoré platí rovnosť (vektorová rovnica má práve jedno riešenie)
, pre ktoré platí rovnosť (vektorová rovnica má práve jedno riešenie)![\small [9, -2, 5]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0) \small [9, -2, 5]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0)](https://lms.umb.sk/filter/tex/pix.php/987fedb1246681eac4577b8596ffe7df.png) resp.
resp. ![\small [4, 1, 6]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0) \small [4, 1, 6]= [1, 3, 2]+ r(2, -1, 1)+ s (1, -1, 0)](https://lms.umb.sk/filter/tex/pix.php/93de6ddda2e4e5ebafc0d01957f5e5fc.png)
Odpoveď: Bod
![\small M = [9, -2, 5] \small M = [9, -2, 5]](https://lms.umb.sk/filter/tex/pix.php/4d2415124dd26dc5ad3d4122c173aa75.png) inciduje s daným podpriestorom, riešenie nájdete
Tu. Ukážte, že bod
inciduje s daným podpriestorom, riešenie nájdete
Tu. Ukážte, že bod ![\small N = [4, 1, 6] \small N = [4, 1, 6]](https://lms.umb.sk/filter/tex/pix.php/f2bd7784e5e4385754858ca3d595e26d.png) neleží v danom podpriestore.
neleží v danom podpriestore. Neparametrické vyjadrenie podpriestoru
V afinnom priestore 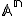 môžeme lineárne podpriestory
môžeme lineárne podpriestory 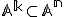 vyjadriť aj neparametricky pomocou sústavy
vyjadriť aj neparametricky pomocou sústavy 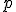 lineárnych rovníc s
lineárnych rovníc s 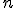 neznámymi.
Ich počet je závislý od dimenzie podpriestoru
neznámymi.
Ich počet je závislý od dimenzie podpriestoru 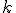 a od dimenzie daného priestoru
a od dimenzie daného priestoru 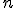 .
Musí byť splnená rovnosť:
.
Musí byť splnená rovnosť: 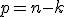 . V stredoškolskej analytickej geometrii
. V stredoškolskej analytickej geometrii
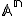 môžeme lineárne podpriestory
môžeme lineárne podpriestory 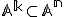 vyjadriť aj neparametricky pomocou sústavy
vyjadriť aj neparametricky pomocou sústavy 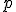 lineárnych rovníc s
lineárnych rovníc s 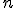 neznámymi.
Ich počet je závislý od dimenzie podpriestoru
neznámymi.
Ich počet je závislý od dimenzie podpriestoru 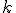 a od dimenzie daného priestoru
a od dimenzie daného priestoru 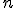 .
Musí byť splnená rovnosť:
.
Musí byť splnená rovnosť: 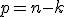 . V stredoškolskej analytickej geometrii
. V stredoškolskej analytickej geometrii
- Priamka (
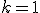 ) ležiaca v rovine (
) ležiaca v rovine (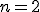 ) je vyjadrená jedinou lineárnou rovnicou s dvoma neznámymi.
Bod (
) je vyjadrená jedinou lineárnou rovnicou s dvoma neznámymi.
Bod (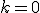 ) je chápaný ako prienik dvoch priamok, teda môže byť vyjadrený ako sústava dvoch lineárnych rovníc.
) je chápaný ako prienik dvoch priamok, teda môže byť vyjadrený ako sústava dvoch lineárnych rovníc. - V afinnom priestore
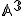 rovina (nadrovina (
rovina (nadrovina (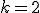 )) je vyjadrená jedinou lineárnou rovnicou s troma neznámymi
)) je vyjadrená jedinou lineárnou rovnicou s troma neznámymi 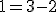 .
Priamka je prienikom dvoch rovín
a na jej určenie sú potrebné dve rovnice
.
Priamka je prienikom dvoch rovín
a na jej určenie sú potrebné dve rovnice  .
.
Príklad 2.
- Nájdite neparametrické vyjadrenie roviny z príkladu 1 a zistite, či body
![\small M = [9, -2, 5], N = [4, 1, 6] \small M = [9, -2, 5], N = [4, 1, 6]](https://lms.umb.sk/filter/tex/pix.php/8a3cde48cba700d2cdcf1f273d3c9937.png) incidujú s touto rovinou.
incidujú s touto rovinou. - Nájdite parametrické aj neparametrické vyjadrenie roviny v
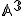 , ktorá prechádza bodom
, ktorá prechádza bodom ![\small A = [1, 2,3] \small A = [1, 2,3]](https://lms.umb.sk/filter/tex/pix.php/d9be5bff457cbec833831928a2dfd25a.png) a má smer
a má smer 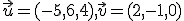 .
.
Riešenie Tu
Vytvorte grafickú ilustrácia k tomuto príkladu.
Pre lineárny podpriestor platí, že s každými dvoma bodmi  obsahuje tento podpriestor aj bod
obsahuje tento podpriestor aj bod
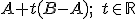 .
.
Dôkaz tohto tvrdenia sa robí v základnom kurze z lineárnej algebry.
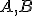 obsahuje tento podpriestor aj bod
obsahuje tento podpriestor aj bod
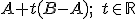 .
.
Dôkaz tohto tvrdenia sa robí v základnom kurze z lineárnej algebry.
Lineárne podpriestory s danou dimenziou.
- Afinný podpriestor dimenzie 1 sa nazýva afinnou priamka.
- Afinný podpriestor dimenzie 2 sa nazýva afinnou rovina.
- Afinný podpriestor dimenzie
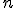 -1 v
-1 v 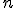 -rozmernom afinnom priestore sa nazýva nadrovina .
Zrejme priamka je zároveň nadrovinou v
priestore
-rozmernom afinnom priestore sa nazýva nadrovina .
Zrejme priamka je zároveň nadrovinou v
priestore 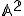 a rovina je nadrovinou v
a rovina je nadrovinou v 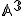 .
. - Budeme hovoriť, že podpriestor
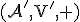 je
je 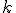 -rozmerný (má dimenziu
-rozmerný (má dimenziu 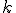 ),
ak podpriestor
),
ak podpriestor 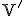 má dimenziu
má dimenziu 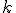 (dim
(dim 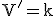 ).
).
Príklady.