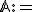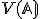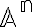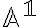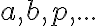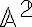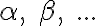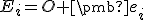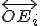Vektorový a afinný priestor
Afinný n-rozmerný priestor
Lineárna súradnicová sústava
Poznámky
Uvedieme základné definície z práce (Monoszová, 1), v ktorých sa pomocou bázy vektorového priestoru zavádza repér afinného priestoru a (lineárna) afinná súradnicová sústava. Súhrnne sa pre tento systém používa označenie: afinný súradnicový systém.
Definície.
- Nech
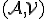 je afinný priestor a
je afinný priestor a 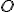 je ľubovoľný bod tohto priestoru. Ďalej nech
je ľubovoľný bod tohto priestoru. Ďalej nech 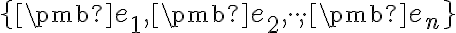 je báza (nie nutne ortonormálna) vektorového priestoru
je báza (nie nutne ortonormálna) vektorového priestoru 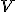 .
Potom
.
Potom 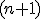 -tica
-tica 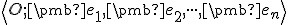 sa nazýva repér afinného priestoru
sa nazýva repér afinného priestoru  .
.
- Nech
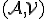 je afinný priestor, nech
je afinný priestor, nech 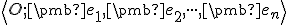 je repér v
je repér v 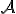 .
Lineárna súradnicová sústava (stručne LSS) je bijektívne zobrazenie
.
Lineárna súradnicová sústava (stručne LSS) je bijektívne zobrazenie
![\small \mathcal {L: A \rightarrow \mathbb R^n}; \; P \rightarrow [p_1,p_2, . . . , p_n], \small \mathcal {L: A \rightarrow \mathbb R^n}; \; P \rightarrow [p_1,p_2, . . . , p_n],](https://lms.umb.sk/filter/tex/pix.php/f2225c4e51903ae901413c224fbda4ef.png)
pričom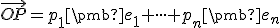 . Pozrite si prácu (str. 8-11) Tu.
. Pozrite si prácu (str. 8-11) Tu.
Dôkaz korektnosti definície.
Ľubovoľný vektor (teda aj polohový) vektorového priestoru sa dá jednoznačne vyjadriť ako lineárna kombinácia vektorov bázy tohto vektorového priestoru
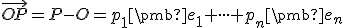 .
.
Z vlastnosti (AP2) vyplýva, že pre bod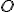 a vektor
a vektor 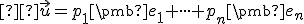 existuje práve jeden bod
existuje práve jeden bod 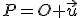 . Preto aj bod
. Preto aj bod  vzhľadom na danú afinnú sústavu súradníc sa dá jednoznačne vyjadriť ako kombinácia
vzhľadom na danú afinnú sústavu súradníc sa dá jednoznačne vyjadriť ako kombinácia
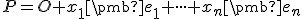 .
.
Rovnosť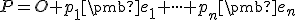 skrátene zapisujeme ako
skrátene zapisujeme ako ![\small P = [p_1,p_2, . . . , p_n] \small P = [p_1,p_2, . . . , p_n]](https://lms.umb.sk/filter/tex/pix.php/cd3bff3cdd6edb7bc37b5e2308304fc3.png) a
a 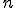 -ticu
-ticu
![[\small p_1,p_2, . . . , p_n] [\small p_1,p_2, . . . , p_n]](https://lms.umb.sk/filter/tex/pix.php/fc0298f4a320aad14ca87bd805d6a0ec.png)
nazývame súradnicami bodu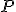 . Súradnice bodu budeme zapisovať v hranatých zátvorkách
. Súradnice bodu budeme zapisovať v hranatých zátvorkách ![\pmb{ [\small x_1,x_2, . . . , x_n] } \pmb{ [\small x_1,x_2, . . . , x_n] }](https://lms.umb.sk/filter/tex/pix.php/8be3a9e49438bc054ad1d97cb87bcdc4.png) .
Vektor, ktorý určuje lineárna kombinácia
.
Vektor, ktorý určuje lineárna kombinácia 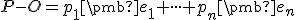 sa nazýva polohový
vektor
sa nazýva polohový
vektor 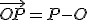 .
.
Ľubovoľný vektor (teda aj polohový) vektorového priestoru sa dá jednoznačne vyjadriť ako lineárna kombinácia vektorov bázy tohto vektorového priestoru
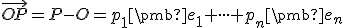 .
.
Z vlastnosti (AP2) vyplýva, že pre bod
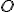 a vektor
a vektor 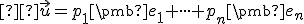 existuje práve jeden bod
existuje práve jeden bod 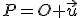 . Preto aj bod
. Preto aj bod  vzhľadom na danú afinnú sústavu súradníc sa dá jednoznačne vyjadriť ako kombinácia
vzhľadom na danú afinnú sústavu súradníc sa dá jednoznačne vyjadriť ako kombinácia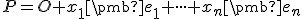 .
.
Rovnosť
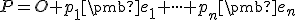 skrátene zapisujeme ako
skrátene zapisujeme ako ![\small P = [p_1,p_2, . . . , p_n] \small P = [p_1,p_2, . . . , p_n]](https://lms.umb.sk/filter/tex/pix.php/cd3bff3cdd6edb7bc37b5e2308304fc3.png) a
a 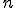 -ticu
-ticu
![[\small p_1,p_2, . . . , p_n] [\small p_1,p_2, . . . , p_n]](https://lms.umb.sk/filter/tex/pix.php/fc0298f4a320aad14ca87bd805d6a0ec.png)
nazývame súradnicami bodu
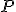 . Súradnice bodu budeme zapisovať v hranatých zátvorkách
. Súradnice bodu budeme zapisovať v hranatých zátvorkách ![\pmb{ [\small x_1,x_2, . . . , x_n] } \pmb{ [\small x_1,x_2, . . . , x_n] }](https://lms.umb.sk/filter/tex/pix.php/8be3a9e49438bc054ad1d97cb87bcdc4.png) .
Vektor, ktorý určuje lineárna kombinácia
.
Vektor, ktorý určuje lineárna kombinácia 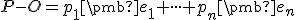 sa nazýva polohový
vektor
sa nazýva polohový
vektor 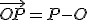 .
.
Existencia a jednoznačnosť súradníc bodu 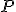 vyplýva tiež z jednoznačného riešenia rovnice,
vyplýva tiež z jednoznačného riešenia rovnice,
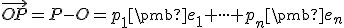 ,
,
keďže vektory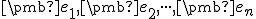 tvoria bázu vektorového priestoru
tvoria bázu vektorového priestoru 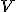 .
.
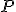 vyplýva tiež z jednoznačného riešenia rovnice,
vyplýva tiež z jednoznačného riešenia rovnice,
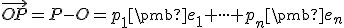 ,
,keďže vektory
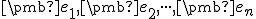 tvoria bázu vektorového priestoru
tvoria bázu vektorového priestoru 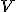 .
.
Pomenovania .
Cvičenie.
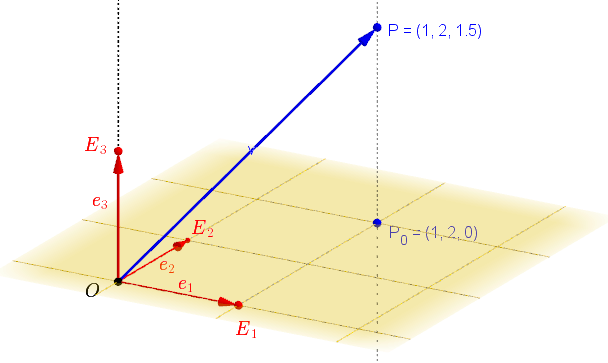
Ukážte, že usporiadaná trojica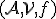 je afinný priestor, ak
je afinný priestor, ak ![\small {\mathcal {A}} = \lbrace{ [x_1,x_2] \in R;x_2=x_1^2 }\rbrace , V=R, f( [x_1,x_2], [y_1,y_2])=x_1-y_1 \small {\mathcal {A}} = \lbrace{ [x_1,x_2] \in R;x_2=x_1^2 }\rbrace , V=R, f( [x_1,x_2], [y_1,y_2])=x_1-y_1](https://lms.umb.sk/filter/tex/pix.php/9b51468f45ac88b2ac91fe89d74d4074.png) . Zistite. či zobrazenie
. Zistite. či zobrazenie ![\small \mathcal {L: A \rightarrow \mathbb R^1}; \; \mathcal {L}( [x_1,x_2])=1+x_1 \small \mathcal {L: A \rightarrow \mathbb R^1}; \; \mathcal {L}( [x_1,x_2])=1+x_1](https://lms.umb.sk/filter/tex/pix.php/d08ad3901ed89daea6bc657e89a5dec3.png) je lineárna sústava súradníc.
je lineárna sústava súradníc.
Ukážte, že usporiadaná trojica
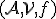 je afinný priestor, ak
je afinný priestor, ak ![\small {\mathcal {A}} = \lbrace{ [x_1,x_2] \in R;x_2=x_1^2 }\rbrace , V=R, f( [x_1,x_2], [y_1,y_2])=x_1-y_1 \small {\mathcal {A}} = \lbrace{ [x_1,x_2] \in R;x_2=x_1^2 }\rbrace , V=R, f( [x_1,x_2], [y_1,y_2])=x_1-y_1](https://lms.umb.sk/filter/tex/pix.php/9b51468f45ac88b2ac91fe89d74d4074.png) . Zistite. či zobrazenie
. Zistite. či zobrazenie ![\small \mathcal {L: A \rightarrow \mathbb R^1}; \; \mathcal {L}( [x_1,x_2])=1+x_1 \small \mathcal {L: A \rightarrow \mathbb R^1}; \; \mathcal {L}( [x_1,x_2])=1+x_1](https://lms.umb.sk/filter/tex/pix.php/d08ad3901ed89daea6bc657e89a5dec3.png) je lineárna sústava súradníc.
je lineárna sústava súradníc.
Riešenie.
- Ľubovoľný bod
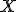 afinného priestoru má súradnice
afinného priestoru má súradnice ![[x,x^2] [x,x^2]](https://lms.umb.sk/filter/tex/pix.php/2a47aadc07cd7da43f678ac9b8e00ec6.png) . Množina všetkých bodov afinného priestoru
. Množina všetkých bodov afinného priestoru 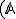 je parabola (nakreslite graf v GeoGebre).
je parabola (nakreslite graf v GeoGebre). - Podmienka (AP1) pre body
![\small X[x,x^2],Y[y,y^2],Z[z,z^2] \small X[x,x^2],Y[y,y^2],Z[z,z^2]](https://lms.umb.sk/filter/tex/pix.php/a9da4bf39fa9cfcb66460afedc953ec4.png) zrejme platí, lebo
zrejme platí, lebo 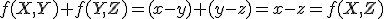 .
. - Podmienka (AP2): Zvoľme si ľubovoľné reálne čísla
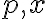 a body
a body ![\small P[p,p^2],X[x,x^2] \small P[p,p^2],X[x,x^2]](https://lms.umb.sk/filter/tex/pix.php/ca8b4484aad29d6e0f414858bbb2a43d.png) , potom zobrazenie
, potom zobrazenie 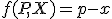 je bijekcia.
je bijekcia. - Zrejme aj zobrazenie
![\small \mathcal {L: A \rightarrow \mathbb R^1}; \; \mathcal {L}( [x,x^2])=1+x \small \mathcal {L: A \rightarrow \mathbb R^1}; \; \mathcal {L}( [x,x^2])=1+x](https://lms.umb.sk/filter/tex/pix.php/0fc66a8834cd1025d9c5b8cd14f37a99.png) je bijektívne, preto je LSS.
je bijektívne, preto je LSS.