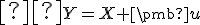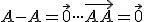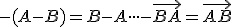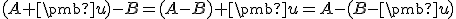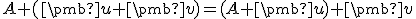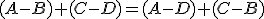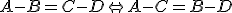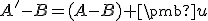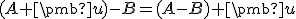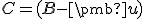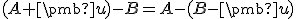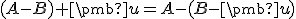Vektorový a afinný priestor
Afinný n-rozmerný priestor
Pri syntetickom prístupe v geometrii sme vychádzame z euklidovského priestoru podľa Euklidových Základov, v ktorom sa základné geometrické útvary (bod, priamka) nedefinovali.
Vedeli sme jednoznačne rozhodnúť o pravdivosti výrokov typu: Bod patrí alebo nepatrí danému útvaru.
Tento prístup z matematického hľadiska predstavuje zásadný problém: Nevieme jasne zadefinovať, čo je to (bodová) množina.
Neskôr (aj historicky) sme zaviedli pojmy:
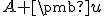
v afinnom priestore predstavuje posunutý bod o vektor
o vektor 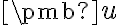 .
.
V tejto kapitole budeme využívať prevažne štandardnú bázu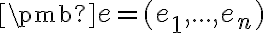 , ktorej vektory sú navzájom kolmé a majú
jednotkovú dĺžku. Takejto báze tiež hovoríme ortonormálová báza.
, ktorej vektory sú navzájom kolmé a majú
jednotkovú dĺžku. Takejto báze tiež hovoríme ortonormálová báza.
Neskôr (aj historicky) sme zaviedli pojmy:
- vektor a vektorový priestor ako štruktúru s predpísanými binárnymi operáciami
- štandardná báza
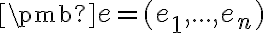 vektorového priestoru
vektorového priestoru 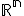
- súradnice vektora
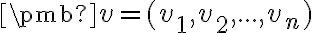 v štandardnej báze.
Tieto pojmy nám umožňujú zaviesť afinný priestor axiomaticky pomocou vektorového priestoru.
v štandardnej báze.
Tieto pojmy nám umožňujú zaviesť afinný priestor axiomaticky pomocou vektorového priestoru.
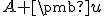
v afinnom priestore predstavuje posunutý bod
 o vektor
o vektor 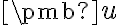 .
.
V tejto kapitole budeme využívať prevažne štandardnú bázu
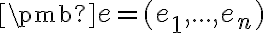 , ktorej vektory sú navzájom kolmé a majú
jednotkovú dĺžku. Takejto báze tiež hovoríme ortonormálová báza.
, ktorej vektory sú navzájom kolmé a majú
jednotkovú dĺžku. Takejto báze tiež hovoríme ortonormálová báza.
Afinný priestor nad poľom 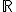 je trojica
je trojica 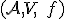 , kde
, kde
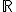 je trojica
je trojica 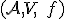 , kde
, kde
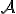 je množina bodov.
je množina bodov.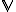 je vektorový priestor nad poľom
je vektorový priestor nad poľom 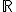 .
.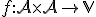 je zobrazenie s vlastnosťami:
je zobrazenie s vlastnosťami:
(AP1)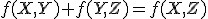
(AP2)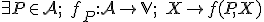
je bijektívne zobrazenie. Pozrite si prácu (príklad 2) Tu.
 Otvorte si applet
Tu.
Otvorte si applet
Tu.
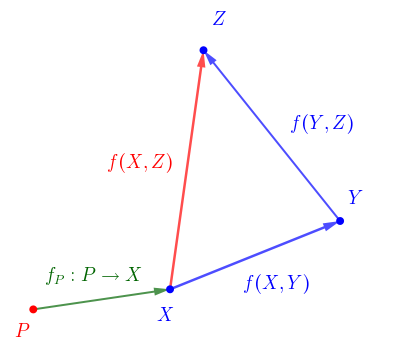
Ak usporiadaná dvojica bodov 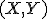 predstavuje umiestnenie vektora
predstavuje umiestnenie vektora 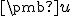 , tak vektor môžeme vyjadriť
ako
, tak vektor môžeme vyjadriť
ako 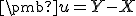 , čo predstavuje zobrazenie
, čo predstavuje zobrazenie
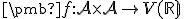 .
.
Podmienka (AP2) sa niekedy uvádza takto:
(AP2')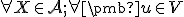 existuje práve jeden
bod
existuje práve jeden
bod 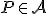 taký, že
taký, že 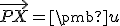 .
.
(AP2'')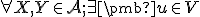 taký, že
taký, že 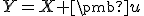 .
.
V tejto kapitole budeme pracovať len s reálnym afinným priestorom nad telesom (poľom) reálnych čísel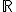 . Fundamentálnou vlastnosťou
afinného bodového priestoru je axiomatické tvrdenie:
. Fundamentálnou vlastnosťou
afinného bodového priestoru je axiomatické tvrdenie:
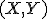 predstavuje umiestnenie vektora
predstavuje umiestnenie vektora 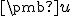 , tak vektor môžeme vyjadriť
ako
, tak vektor môžeme vyjadriť
ako 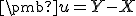 , čo predstavuje zobrazenie
, čo predstavuje zobrazenie
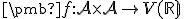 .
.
Podmienka (AP2) sa niekedy uvádza takto:
(AP2')
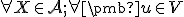 existuje práve jeden
bod
existuje práve jeden
bod 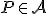 taký, že
taký, že 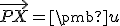 .
.
(AP2'')
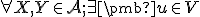 taký, že
taký, že 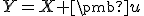 .
.
V tejto kapitole budeme pracovať len s reálnym afinným priestorom nad telesom (poľom) reálnych čísel
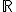 . Fundamentálnou vlastnosťou
afinného bodového priestoru je axiomatické tvrdenie:
. Fundamentálnou vlastnosťou
afinného bodového priestoru je axiomatické tvrdenie:
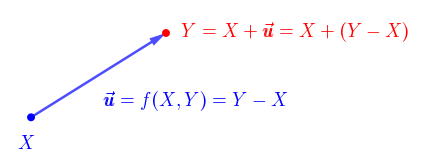 Applet hyperbola Tu.
Applet hyperbola Tu.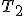 : V afinnom priestore
: V afinnom priestore 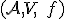 platí vlastnost’ (AP2) pre ľubovoľný pevne zvolený bod
platí vlastnost’ (AP2) pre ľubovoľný pevne zvolený bod 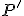 ,
t.j.
,
t.j. 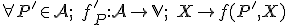 je bijektívne zobrazenie. Stačí si uvedomiť, že
je bijektívne zobrazenie. Stačí si uvedomiť, že 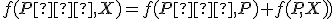 .
.
Zistite, či usporiadané trojice 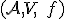 sú afinným priestorom.
sú afinným priestorom.
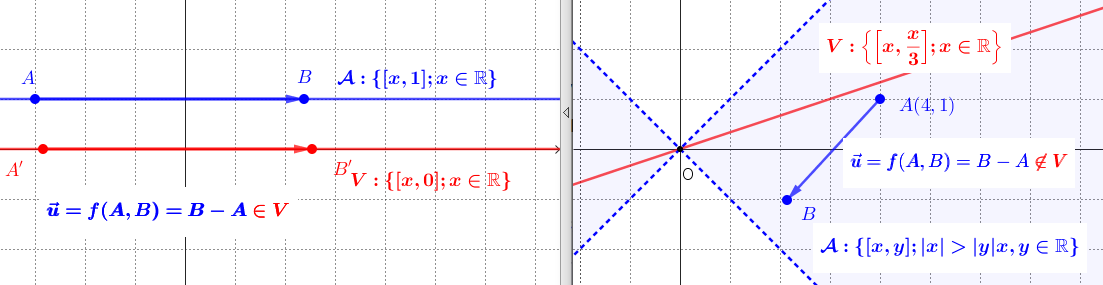
Otvorte si dynamické obrázky: ľavý Tu - príklad afinného priestoru; pravý Tu - nie je afinným priestorom.
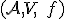 sú afinným priestorom.
sú afinným priestorom.
Otvorte si dynamické obrázky: ľavý Tu - príklad afinného priestoru; pravý Tu - nie je afinným priestorom.
Poznámky.
- Afinný priestor budeme tiež jednoducho označovať
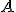 alebo ako
alebo ako 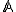 .
Vektorový priestor prislúchajúci afinnému priestoru
.
Vektorový priestor prislúchajúci afinnému priestoru 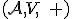 budeme označovať ako
budeme označovať ako 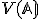 alebo len
alebo len 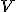 .
. - Vektorovému priestoru hovoríme tiež zameranie afinného priestoru. Afinný priestor, ktorého zameraním je vektorový priestor nad poľom reálnych čísel nazývame reálny afinný priestor alebo aj aritmetický afinný priestor.
- Affinis znamená latinsky príbuzný. Prvý krát tento pojem použil Leonhard Euler (1707-1783) pre označenie vzťahu vzoru a obrazu v zobrazení, ktoré zachováva deliaci pomer (pozri kapitolu Deliaci pomer Tu). Afinná geometria je geometria bez vzdialenosti/miery.
Príklad.
Dané sú množiny (červená)
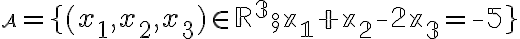 ,
,
množina (modrá)
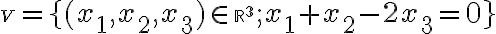
a zobrazenie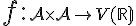 je odčitovanie trojíc reálnych čísel po zložkách.
je odčitovanie trojíc reálnych čísel po zložkách.
Dokážte, že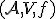 je afinný priestor nad poľom
je afinný priestor nad poľom 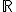 .
Dynamický obrázok Tu.
.
Dynamický obrázok Tu.
Dané sú množiny (červená)
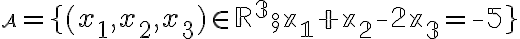 ,
,
množina (modrá)
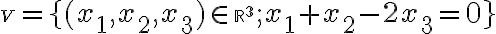
a zobrazenie
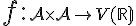 je odčitovanie trojíc reálnych čísel po zložkách.
je odčitovanie trojíc reálnych čísel po zložkách.
Dokážte, že
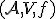 je afinný priestor nad poľom
je afinný priestor nad poľom 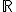 .
Dynamický obrázok Tu.
.
Dynamický obrázok Tu.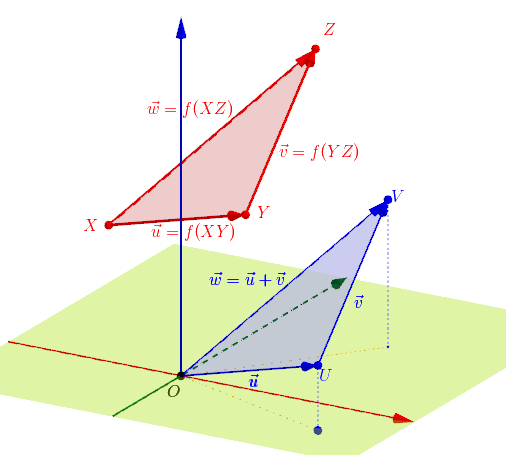
Riešenie.
Pre ľubovoľný bod![\small X[x_1,x_2,x_3] \in \mathcal{A} \small X[x_1,x_2,x_3] \in \mathcal{A}](https://lms.umb.sk/filter/tex/pix.php/1e32b09cf88a45e990cb4c781e1264a3.png) platí, že
platí, že 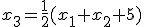 .
.
Pre ľubovoľný bod
![\small X[x_1,x_2,x_3] \in \mathcal{A} \small X[x_1,x_2,x_3] \in \mathcal{A}](https://lms.umb.sk/filter/tex/pix.php/1e32b09cf88a45e990cb4c781e1264a3.png) platí, že
platí, že 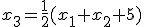 .
.
- Podmienka (AP1): zo vzťahov
![\small f(X,Y)=\left [x_1-y_1,x_2-y_2,x_3-y_3 \right ] =\left [ x_1-y_1,x_2-y_2, \frac{1}{2} \left\{(x_1-y_1 )+(x_2-y_2 ) \right\} \right ] \small f(X,Y)=\left [x_1-y_1,x_2-y_2,x_3-y_3 \right ] =\left [ x_1-y_1,x_2-y_2, \frac{1}{2} \left\{(x_1-y_1 )+(x_2-y_2 ) \right\} \right ]](https://lms.umb.sk/filter/tex/pix.php/212ddeb0870fc8fd963a34c97efd0b5e.png)
![\small f(Y,Z)=\left [y_1-z_1,\;y_2-z_2,y_3-z_3 \right ]=\left [y_1-z_1,\;y_2-z_2, \frac{1}{2} \left\{(y_1-z_1 )+(y_2-z_2 )\right\} \right ] \small f(Y,Z)=\left [y_1-z_1,\;y_2-z_2,y_3-z_3 \right ]=\left [y_1-z_1,\;y_2-z_2, \frac{1}{2} \left\{(y_1-z_1 )+(y_2-z_2 )\right\} \right ]](https://lms.umb.sk/filter/tex/pix.php/b8e2befaa385d58e1495d0dda24dd2d8.png)
dostávame![\small f(X,Z)=\left [ x_1-z_1,x_2-z_2, \frac{1}{2} ((x_1-z_1 )+(x_2-z_2 )) \right ] \small f(X,Z)=\left [ x_1-z_1,x_2-z_2, \frac{1}{2} ((x_1-z_1 )+(x_2-z_2 )) \right ]](https://lms.umb.sk/filter/tex/pix.php/1b18ee33757839b8a6461582719e1a95.png) ,
,
čo bolo treba ukázať. - Podmienka (AP2): Nech
![\small P=[p_1,p_2, \frac{1}{2} (p_1+p_2+5)] \small P=[p_1,p_2, \frac{1}{2} (p_1+p_2+5)]](https://lms.umb.sk/filter/tex/pix.php/09702c0c73bf5072e288f185b849edb3.png) je pevne zvolený bod
a
je pevne zvolený bod
a ![\small X=[x_1,x_2, \frac{1}{2} (x_1+x_2+5)], Y=[y_1,y_2, \frac{1}{2} (x_1+x_2+5)] \small X=[x_1,x_2, \frac{1}{2} (x_1+x_2+5)], Y=[y_1,y_2, \frac{1}{2} (x_1+x_2+5)]](https://lms.umb.sk/filter/tex/pix.php/b45741f780d3658c11d776d825c1471b.png) sú ľubovoľné dva rôzne body.
sú ľubovoľné dva rôzne body.
Potom je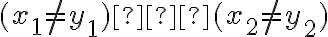 a zrejme aj pre obrazy
a zrejme aj pre obrazy
![\small f(P,X)=\left [p_1-x_1,p_2-x_2,\frac{1}{2} ((p_1-x_1 )+(p_2-x_2 )) \right ] \small f(P,X)=\left [p_1-x_1,p_2-x_2,\frac{1}{2} ((p_1-x_1 )+(p_2-x_2 )) \right ]](https://lms.umb.sk/filter/tex/pix.php/63009f454440a8eae526eb94e04d07d7.png)
![\small f(P,Y)=\left [ p_1-y_1,p_2-y_2,\frac{1}{2} ((p_1-y_1 )+(p_2-y_2 )) \right ] \small f(P,Y)=\left [ p_1-y_1,p_2-y_2,\frac{1}{2} ((p_1-y_1 )+(p_2-y_2 )) \right ]](https://lms.umb.sk/filter/tex/pix.php/596431e055367812dc5b1a41713657dd.png)
platí, že sú rôzne. Teda zobrazenie je bijektívne.
Dôkaz, pre podmienku (AP2') nájdete v práci Afinné transformácie na strane 7. Pozrite tiež Príklad 2 na strane 8.
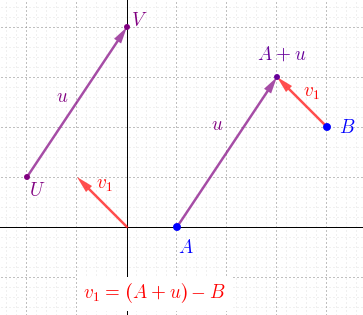
Tvrdenie (operácie s bodmi).
Nech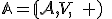 je afinný priestor s operáciou
je afinný priestor s operáciou 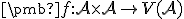 . Potom pre body
. Potom pre body 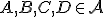 Interpretujte tieto vzťahy v klasickej euklidovskej rovine pomocou programu GeoGebra.
Interpretujte tieto vzťahy v klasickej euklidovskej rovine pomocou programu GeoGebra.
Nech
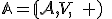 je afinný priestor s operáciou
je afinný priestor s operáciou 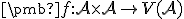 . Potom pre body
. Potom pre body 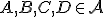 Interpretujte tieto vzťahy v klasickej euklidovskej rovine pomocou programu GeoGebra.
Interpretujte tieto vzťahy v klasickej euklidovskej rovine pomocou programu GeoGebra.
Dôkaz.
-
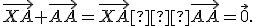
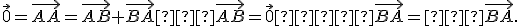
- Označme
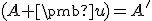 .
.
- Z vlastnosti (AP1) dostávame
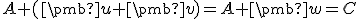 . Na druhej strane
. Na druhej strane 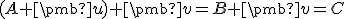 .
. - Dôkazy ďalších tvrdení nájdete napríklad v práci [Duplák, J.: Afinná a Euklidovská geometria.]