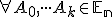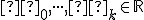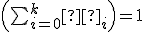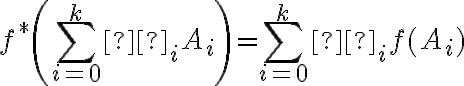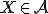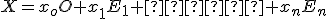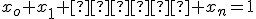Vektorový a afinný priestor
Afinné zobrazenie
Jednoznačnosť AZ
Afinné zobrazenie 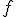 determinuje ďalšie zobrazenie
determinuje ďalšie zobrazenie 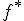 medzi vektorovými zložkami príslušných euklidovských vektorových priestorov.
medzi vektorovými zložkami príslušných euklidovských vektorových priestorov.
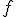 determinuje ďalšie zobrazenie
determinuje ďalšie zobrazenie 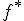 medzi vektorovými zložkami príslušných euklidovských vektorových priestorov.
medzi vektorovými zložkami príslušných euklidovských vektorových priestorov.
Definícia - asociované zobrazenie.
Nech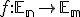 je afinné zobrazenie. Zobrazenie
je afinné zobrazenie. Zobrazenie 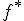 nazývame asociovaným zobrazením k afinnému zobrazeniu
nazývame asociovaným zobrazením k afinnému zobrazeniu 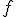 ,
ak spĺňa nasledujúce podmienky:
,
ak spĺňa nasledujúce podmienky:
Nech
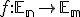 je afinné zobrazenie. Zobrazenie
je afinné zobrazenie. Zobrazenie 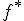 nazývame asociovaným zobrazením k afinnému zobrazeniu
nazývame asociovaným zobrazením k afinnému zobrazeniu 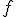 ,
ak spĺňa nasledujúce podmienky:
,
ak spĺňa nasledujúce podmienky:
Predchádzajúca definícia vlastne hovorí, že asociované zobrazenie „zachováva” lineárne kombinácie bodov.
Veta - korektnosť definície asociovaného zobrazenia.
Zobrazenie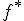 je jednoznačné určené a je dobre definované. Ekvivalentný matematický zápis: nech
je jednoznačné určené a je dobre definované. Ekvivalentný matematický zápis: nech
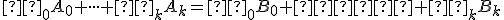
pre nejaké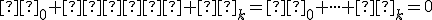 . Potom existuje práve jedno asociované zobrazenie
. Potom existuje práve jedno asociované zobrazenie 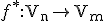 také, že
také, že
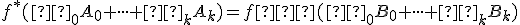 .
.
Zobrazenie
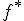 je jednoznačné určené a je dobre definované. Ekvivalentný matematický zápis: nech
je jednoznačné určené a je dobre definované. Ekvivalentný matematický zápis: nech
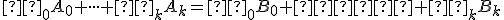
pre nejaké
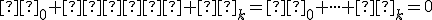 . Potom existuje práve jedno asociované zobrazenie
. Potom existuje práve jedno asociované zobrazenie 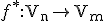 také, že
také, že
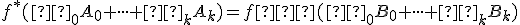 .
.
Dôkaz korektnosť definície asociovaného zobrazenia.
Existencia a jednoznačnosť asociovaného zobrazenia je daná obrazmi vektorov Vn.
Čo sa týka dobrej definovanosti zápisu v definicii asociovaného zobrazenia, z predpokladu vety vyplýva, že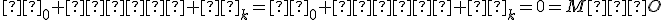 pre nejaké
pre nejaké 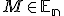 . Teda
. Teda
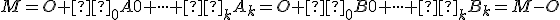 .
.
Keďže zobrazenie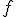 je afinné, a teda zachováva lineárne kombinácie bodov, tak
je afinné, a teda zachováva lineárne kombinácie bodov, tak
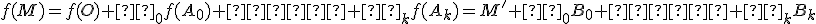 . Prezrite si applet z definície
. Prezrite si applet z definície
Existencia a jednoznačnosť asociovaného zobrazenia je daná obrazmi vektorov Vn.
Čo sa týka dobrej definovanosti zápisu v definicii asociovaného zobrazenia, z predpokladu vety vyplýva, že
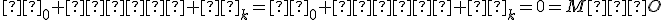 pre nejaké
pre nejaké 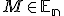 . Teda
. Teda
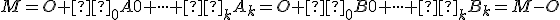 .
.
Keďže zobrazenie
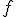 je afinné, a teda zachováva lineárne kombinácie bodov, tak
je afinné, a teda zachováva lineárne kombinácie bodov, tak
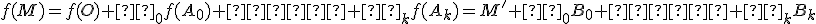 . Prezrite si applet z definície
. Prezrite si applet z definície
Lineárne nezávislá množina bodov.
Nech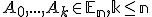 je množina bodov euklidovského priestoru. Je celkom prirodzené zaviesť pojem lineárne nezávislých bodov,
ako množinu lineárne nezávislých vektorov
je množina bodov euklidovského priestoru. Je celkom prirodzené zaviesť pojem lineárne nezávislých bodov,
ako množinu lineárne nezávislých vektorov 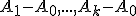 .
.
Nech
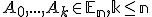 je množina bodov euklidovského priestoru. Je celkom prirodzené zaviesť pojem lineárne nezávislých bodov,
ako množinu lineárne nezávislých vektorov
je množina bodov euklidovského priestoru. Je celkom prirodzené zaviesť pojem lineárne nezávislých bodov,
ako množinu lineárne nezávislých vektorov 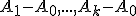 .
.
Poznámka.
Z predchádzajúcej definície je zrejmé, že v euklidovskom rozmernom priestore existuje najviac
rozmernom priestore existuje najviac 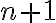 lineárne nezávislých bodov. Naviac tento počet sa dá dosiahnuť.
lineárne nezávislých bodov. Naviac tento počet sa dá dosiahnuť.
Z predchádzajúcej definície je zrejmé, že v euklidovskom
 rozmernom priestore existuje najviac
rozmernom priestore existuje najviac 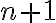 lineárne nezávislých bodov. Naviac tento počet sa dá dosiahnuť.
lineárne nezávislých bodov. Naviac tento počet sa dá dosiahnuť.
V kapitole "Lineárna kombinácia bodov" sme dokázali vetu
Na základe tohto tvrdenia a definície nezávislých bodov, môžeme povedať, že ľubovoľný bod euklidovského priestoru 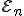 sa dá
jednoznačne vyjadriť ako ich lineárna kombinácia.
sa dá
jednoznačne vyjadriť ako ich lineárna kombinácia.
Poznámka o lineárnych zobrazeniach.
Z lineárnej algebry poznáme tvrdenie, že každé lineárne zobrazenie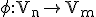 je jednoznačne dané obrazmi prvkov nejakej bázy
priestoru
je jednoznačne dané obrazmi prvkov nejakej bázy
priestoru 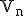 .
.
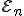 sa dá
jednoznačne vyjadriť ako ich lineárna kombinácia.
sa dá
jednoznačne vyjadriť ako ich lineárna kombinácia.
Poznámka o lineárnych zobrazeniach.
Z lineárnej algebry poznáme tvrdenie, že každé lineárne zobrazenie
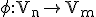 je jednoznačne dané obrazmi prvkov nejakej bázy
priestoru
je jednoznačne dané obrazmi prvkov nejakej bázy
priestoru 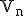 .
.
Dôsledok obraz repéra.
Nech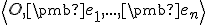 je repér priestoru
je repér priestoru 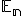 a ľubovoľný bod
a ľubovoľný bod 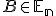 . Ďalej
nech
. Ďalej
nech 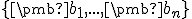 sú vektory vektorového priestoru
sú vektory vektorového priestoru 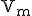 . Potom existuje jediné afinné
zobrazenie
. Potom existuje jediné afinné
zobrazenie 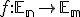 také, že
také, že
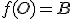 a
a 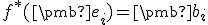 pre
pre 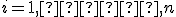 .
.
Nech
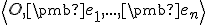 je repér priestoru
je repér priestoru 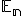 a ľubovoľný bod
a ľubovoľný bod 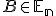 . Ďalej
nech
. Ďalej
nech 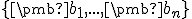 sú vektory vektorového priestoru
sú vektory vektorového priestoru 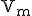 . Potom existuje jediné afinné
zobrazenie
. Potom existuje jediné afinné
zobrazenie 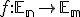 také, že
také, že
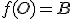 a
a 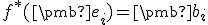 pre
pre 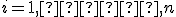 .
.
Dôkaz nájdete v učebniciach z lineárnej algebry.
Veta (Jednoznačnosť afinného zobrazenia).
Nech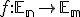 je afinné zobrazenie. Potom
je afinné zobrazenie. Potom 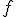 je jednoznačne určené obrazmi
je jednoznačne určené obrazmi 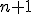 lineárne nezávislých bodov z
lineárne nezávislých bodov z 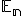 .
.
Nech
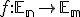 je afinné zobrazenie. Potom
je afinné zobrazenie. Potom 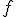 je jednoznačne určené obrazmi
je jednoznačne určené obrazmi 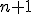 lineárne nezávislých bodov z
lineárne nezávislých bodov z 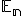 .
.
Dôkaz.
Nech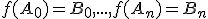 . V súlade s definíciou nezávislých bodov, vektory
. V súlade s definíciou nezávislých bodov, vektory
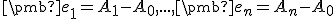
sú lineárne nezávislé. Keďže afinné zobrazenie je zároveň aj lineárne, tak pre obrazy vektorov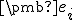 v asociovanom afinnom zobrazení
v asociovanom afinnom zobrazení 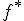 platí
platí
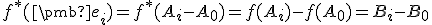 pre
pre 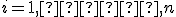 .
.
Podľa dôsledku "obraz repéra" je takto jednoznačne definované afinné zobrazenie. Treba len overiť, či takto definované zobrazenia spĺňa podmienku, že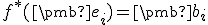 .
.
(Urobte to ako cvičenie!)
Nech
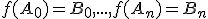 . V súlade s definíciou nezávislých bodov, vektory
. V súlade s definíciou nezávislých bodov, vektory
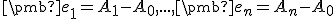
sú lineárne nezávislé. Keďže afinné zobrazenie je zároveň aj lineárne, tak pre obrazy vektorov
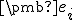 v asociovanom afinnom zobrazení
v asociovanom afinnom zobrazení 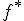 platí
platí
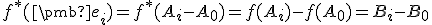 pre
pre 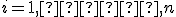 .
.
Podľa dôsledku "obraz repéra" je takto jednoznačne definované afinné zobrazenie. Treba len overiť, či takto definované zobrazenia spĺňa podmienku, že
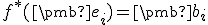 .
.
(Urobte to ako cvičenie!)
Príklad.
Dané sú body afinného priestoru![\small \mathcal{A}_4: A[2, 4, 5, 6]; B[−7, 4, 5, 6]; C[6, 11, 3, 7]; D[−3, −10, 9, 4]; E[−3, 11, 3, 7] \small \mathcal{A}_4: A[2, 4, 5, 6]; B[−7, 4, 5, 6]; C[6, 11, 3, 7]; D[−3, −10, 9, 4]; E[−3, 11, 3, 7]](https://lms.umb.sk/filter/tex/pix.php/9b09fbccf9c7067f710d5ec3a4f09993.png) . Zistite, či sústava
bodov
. Zistite, či sústava
bodov 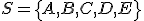 je afinne (ne)závislá a vypočítajte dimenziu afinného podpriestoru generovaného sústavou
je afinne (ne)závislá a vypočítajte dimenziu afinného podpriestoru generovaného sústavou  (dimenziu obalu
(dimenziu obalu  ).
).
Dané sú body afinného priestoru
![\small \mathcal{A}_4: A[2, 4, 5, 6]; B[−7, 4, 5, 6]; C[6, 11, 3, 7]; D[−3, −10, 9, 4]; E[−3, 11, 3, 7] \small \mathcal{A}_4: A[2, 4, 5, 6]; B[−7, 4, 5, 6]; C[6, 11, 3, 7]; D[−3, −10, 9, 4]; E[−3, 11, 3, 7]](https://lms.umb.sk/filter/tex/pix.php/9b09fbccf9c7067f710d5ec3a4f09993.png) . Zistite, či sústava
bodov
. Zistite, či sústava
bodov 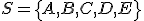 je afinne (ne)závislá a vypočítajte dimenziu afinného podpriestoru generovaného sústavou
je afinne (ne)závislá a vypočítajte dimenziu afinného podpriestoru generovaného sústavou  (dimenziu obalu
(dimenziu obalu  ).
).
Riešenie.
Množina bodov je afinne nezávislá, ak sústava vektorov
je afinne nezávislá, ak sústava vektorov
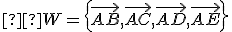
je lineárne nezávislá. Pre súradnice týchto vektorov dostaneme
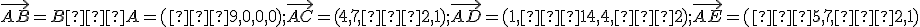 .
.
Sústava vektorov W je lineárne nezávislá, ak rovnosť
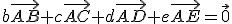
je splnená práve len pre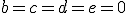 . V našom prípade to nie je splnené lebo hodnosť matice
. V našom prípade to nie je splnené lebo hodnosť matice
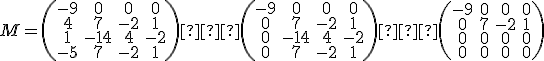
je dva. Teda hodnosť je menšia ako počet vektorov, preto sústava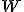 je lineárne závislá a teda body
je lineárne závislá a teda body 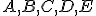 sú afinne závisle. Z poslednej matice vyplýva,
že dva vektory
sú afinne závisle. Z poslednej matice vyplýva,
že dva vektory 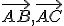 sú lineárne nezávislé a vektory
sú lineárne nezávislé a vektory 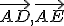 sú ich lineárne kombinácie.
Preto dimenzia podpriestoru
sú ich lineárne kombinácie.
Preto dimenzia podpriestoru 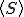 je rovná dvom. Parametrické vyjadrenie tohto podpriestoru môžeme vyjadriť ako
je rovná dvom. Parametrické vyjadrenie tohto podpriestoru môžeme vyjadriť ako
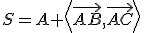 .
.
To znamená, že body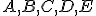 ležia v rovine
ležia v rovine 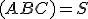 .
.
Množina bodov
 je afinne nezávislá, ak sústava vektorov
je afinne nezávislá, ak sústava vektorov
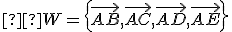
je lineárne nezávislá. Pre súradnice týchto vektorov dostaneme
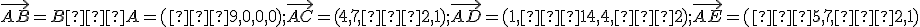 .
.
Sústava vektorov W je lineárne nezávislá, ak rovnosť
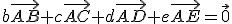
je splnená práve len pre
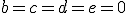 . V našom prípade to nie je splnené lebo hodnosť matice
. V našom prípade to nie je splnené lebo hodnosť matice
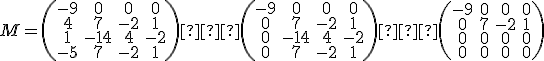
je dva. Teda hodnosť je menšia ako počet vektorov, preto sústava
 je lineárne závislá a teda body
je lineárne závislá a teda body  sú afinne závisle. Z poslednej matice vyplýva,
že dva vektory
sú afinne závisle. Z poslednej matice vyplýva,
že dva vektory  sú lineárne nezávislé a vektory
sú lineárne nezávislé a vektory 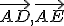 sú ich lineárne kombinácie.
Preto dimenzia podpriestoru
sú ich lineárne kombinácie.
Preto dimenzia podpriestoru 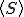 je rovná dvom. Parametrické vyjadrenie tohto podpriestoru môžeme vyjadriť ako
je rovná dvom. Parametrické vyjadrenie tohto podpriestoru môžeme vyjadriť ako
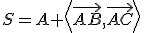 .
.
To znamená, že body
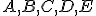 ležia v rovine
ležia v rovine 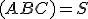 .
.
Poznámky.
- Nech
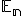 je
je 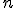 -rozmerný euklidovský priestor so zameraním
-rozmerný euklidovský priestor so zameraním 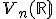 a
nech
a
nech 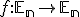 je afinná transformácia. Potom môžeme definovať asociované zobrazenie
je afinná transformácia. Potom môžeme definovať asociované zobrazenie 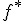 afinného zobrazenia
afinného zobrazenia  aj nasledovne:
aj nasledovne:
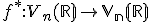 ,
, 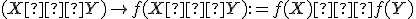
- Asociované zobrazenie
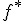 je vlastne "reštrikcia" zobrazenia
je vlastne "reštrikcia" zobrazenia  na vektorový priestor. Zobrazuje vektory
so zamerania
na vektorový priestor. Zobrazuje vektory
so zamerania 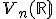 na vektory toho istého zamerania.
na vektory toho istého zamerania.