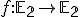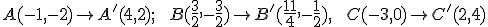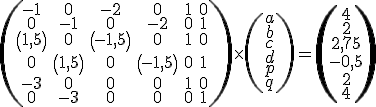Vektorový a afinný priestor
Analytické vyjadrenie
Obraz troch bodov
Nech je daná 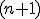 - tica bodov
- tica bodov 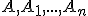 v euklidovskom priestore
v euklidovskom priestore 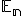 taká, že
taká, že 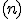 - tica vektorov
- tica vektorov 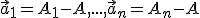 so zamerania
so zamerania 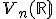 je nezávislá. V tomto prípade sústava
je nezávislá. V tomto prípade sústava 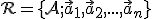 tvorí repér tohto priestoru. Takejto
tvorí repér tohto priestoru. Takejto 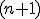 - tici bodov budeme hovoriť, že je lineárne nezávislá.
- tici bodov budeme hovoriť, že je lineárne nezávislá.
Vo vete "Jednoznačnosť afinného zobrazenia" sme dokázali, že afinné zobrazenie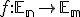 je jednoznačne určené obrazmi
je jednoznačne určené obrazmi 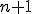 lineárne nezávislých bodov euklidovského priestoru
lineárne nezávislých bodov euklidovského priestoru 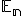 .Dôkaz tohto tvrdenia nájdete aj v práci [Chalmoviansky, 2022].
.Dôkaz tohto tvrdenia nájdete aj v práci [Chalmoviansky, 2022].
V ďalšej časti sa zameriame na určenie transformačných rovníc afinného zobrazenia v euklidovskej rovine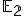 , v ktorom sú dané dve trojice odpovedajúcich nekolineárnych bodov. Začneme trojicami, ktoré vyhovujú rovnoľahlosti, čo nám uľahčí kontrolu správnosti určenia transformačných rovníc.
, v ktorom sú dané dve trojice odpovedajúcich nekolineárnych bodov. Začneme trojicami, ktoré vyhovujú rovnoľahlosti, čo nám uľahčí kontrolu správnosti určenia transformačných rovníc.
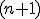 - tica bodov
- tica bodov 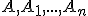 v euklidovskom priestore
v euklidovskom priestore 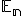 taká, že
taká, že  - tica vektorov
- tica vektorov 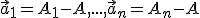 so zamerania
so zamerania 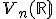 je nezávislá. V tomto prípade sústava
je nezávislá. V tomto prípade sústava 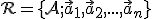 tvorí repér tohto priestoru. Takejto
tvorí repér tohto priestoru. Takejto 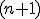 - tici bodov budeme hovoriť, že je lineárne nezávislá.
- tici bodov budeme hovoriť, že je lineárne nezávislá.
Vo vete "Jednoznačnosť afinného zobrazenia" sme dokázali, že afinné zobrazenie
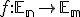 je jednoznačne určené obrazmi
je jednoznačne určené obrazmi 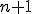 lineárne nezávislých bodov euklidovského priestoru
lineárne nezávislých bodov euklidovského priestoru 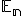 .Dôkaz tohto tvrdenia nájdete aj v práci [Chalmoviansky, 2022].
.Dôkaz tohto tvrdenia nájdete aj v práci [Chalmoviansky, 2022].
V ďalšej časti sa zameriame na určenie transformačných rovníc afinného zobrazenia v euklidovskej rovine
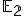 , v ktorom sú dané dve trojice odpovedajúcich nekolineárnych bodov. Začneme trojicami, ktoré vyhovujú rovnoľahlosti, čo nám uľahčí kontrolu správnosti určenia transformačných rovníc.
, v ktorom sú dané dve trojice odpovedajúcich nekolineárnych bodov. Začneme trojicami, ktoré vyhovujú rovnoľahlosti, čo nám uľahčí kontrolu správnosti určenia transformačných rovníc.
Riešenie (riešenie pomocou programu GeoGebra
Tu).
Pre bod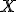 v rovine
v rovine 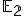 platí, že je lineárnou kombináciou bodov
platí, že je lineárnou kombináciou bodov 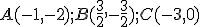 ,
preto platí
,
preto platí
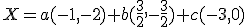 , pričom
, pričom 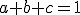 .
.
V kapitole "Afinné zobrazenie" sme ukázali, že transformačné rovnice afinného zobrazenia v euklidovskom priestore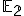 majú tvar
majú tvar
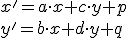 ,
,
kde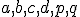 sú súradnice obrazov vektorov bázy
sú súradnice obrazov vektorov bázy 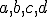 a súradnice obrazu začiatku repéra
a súradnice obrazu začiatku repéra 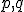 . Dosaďme súradnice
bodov
. Dosaďme súradnice
bodov 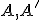 do týchto transformačných rovníc. Po úprave dostaneme dve rovnice o 6 neznámych
do týchto transformačných rovníc. Po úprave dostaneme dve rovnice o 6 neznámych 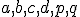 . Konkrétne to budú rovnice
. Konkrétne to budú rovnice
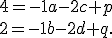
Postupne ak dosadíme súradnice ďalších bodov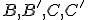 dostaneme ďalšie 4 rovnice.
dostaneme ďalšie 4 rovnice.
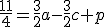
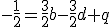
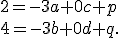
Spolu je to sústava 6 lineárnych rovníc, ktorá vzhľadom na zadanie (nekolineárne body) bude mať práve jedno riešenie. Vypíšte všetkých 6 rovníc a potom vyriešte túto sústavu.
Pre bod
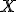 v rovine
v rovine 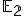 platí, že je lineárnou kombináciou bodov
platí, že je lineárnou kombináciou bodov 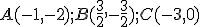 ,
preto platí
,
preto platí
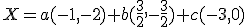 , pričom
, pričom 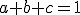 .
.
V kapitole "Afinné zobrazenie" sme ukázali, že transformačné rovnice afinného zobrazenia v euklidovskom priestore
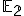 majú tvar
majú tvar
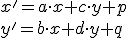 ,
,
kde
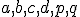 sú súradnice obrazov vektorov bázy
sú súradnice obrazov vektorov bázy 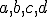 a súradnice obrazu začiatku repéra
a súradnice obrazu začiatku repéra 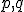 . Dosaďme súradnice
bodov
. Dosaďme súradnice
bodov 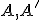 do týchto transformačných rovníc. Po úprave dostaneme dve rovnice o 6 neznámych
do týchto transformačných rovníc. Po úprave dostaneme dve rovnice o 6 neznámych 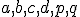 . Konkrétne to budú rovnice
. Konkrétne to budú rovnice
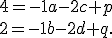
Postupne ak dosadíme súradnice ďalších bodov
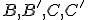 dostaneme ďalšie 4 rovnice.
dostaneme ďalšie 4 rovnice.
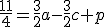
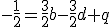
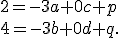
Spolu je to sústava 6 lineárnych rovníc, ktorá vzhľadom na zadanie (nekolineárne body) bude mať práve jedno riešenie. Vypíšte všetkých 6 rovníc a potom vyriešte túto sústavu.
Poznámka.
Nájsť riešenie takejto sústavy je časovo dosť náročná práca, ktorá študentov nemotivuje a navyše ich odpúta od podstaty úlohy– nájsť transformačné rovnice.
Preto s výhodou môžeme použiť nástroje programu GeoGebra (alebo iných softvérov, napr. Matrix). Pomocou GeoGebra vzhľadu "Tabuľka" najskôr „vygenerujeme“ maticu sústavy 6 rovníc so 6 neznámymi s pravou stranou. Do jednotlivých polí v „Tabuľke“ vložíme súradnice bodov pomocou príkazov: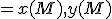 , kde
, kde  je názov bodu, ktorého súadnice vkladáme.
je názov bodu, ktorého súadnice vkladáme.
Z tabuľky vidieť, že napr. do poľa „A2“ je vložený príkaz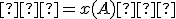 , ktorý predstavuje prvú súradnicu bodu
, ktorý predstavuje prvú súradnicu bodu 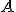 .
Tabuľka má ďalšiu veľkú výhodu: Vstupné pole „A2“ je aktívne voči zmene polohy bodu
.
Tabuľka má ďalšiu veľkú výhodu: Vstupné pole „A2“ je aktívne voči zmene polohy bodu 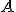 . Ak sa poloha bodu
. Ak sa poloha bodu 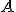 zmení, tak sa automaticky zmení aj
príslušné polia tabuľky
zmení, tak sa automaticky zmení aj
príslušné polia tabuľky 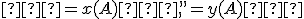 . Analogicky sa aktualizujú aj zvyšné polia tabuľky. Dynamické vstupy nám teda umožnia aktualizovať maticu
sústavy 6 rovníc aj s pravou stranou. Je to matica typu 6×7 s rozsahom je
. Analogicky sa aktualizujú aj zvyšné polia tabuľky. Dynamické vstupy nám teda umožnia aktualizovať maticu
sústavy 6 rovníc aj s pravou stranou. Je to matica typu 6×7 s rozsahom je 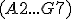 .
.
Riešenie danej sústavy 6 rovníc so 6 neznámymi s pravou stranou môžeme nájsť pomocou maticového počtu, ktorý je tiež k dispozícii v GeoGebre.
Výsledok.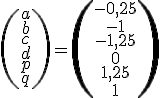
Transformačné rovnice skúmaného afinného zobrazenia sú prezentované na ďalšom obrázku v ľavej časti obrázka.
Matica zobrazenia Nájsť riešenie takejto sústavy je časovo dosť náročná práca, ktorá študentov nemotivuje a navyše ich odpúta od podstaty úlohy– nájsť transformačné rovnice.
Preto s výhodou môžeme použiť nástroje programu GeoGebra (alebo iných softvérov, napr. Matrix). Pomocou GeoGebra vzhľadu "Tabuľka" najskôr „vygenerujeme“ maticu sústavy 6 rovníc so 6 neznámymi s pravou stranou. Do jednotlivých polí v „Tabuľke“ vložíme súradnice bodov pomocou príkazov:
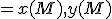 , kde
, kde  je názov bodu, ktorého súadnice vkladáme.
je názov bodu, ktorého súadnice vkladáme.
Z tabuľky vidieť, že napr. do poľa „A2“ je vložený príkaz
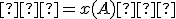 , ktorý predstavuje prvú súradnicu bodu
, ktorý predstavuje prvú súradnicu bodu 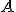 .
Tabuľka má ďalšiu veľkú výhodu: Vstupné pole „A2“ je aktívne voči zmene polohy bodu
.
Tabuľka má ďalšiu veľkú výhodu: Vstupné pole „A2“ je aktívne voči zmene polohy bodu 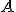 . Ak sa poloha bodu
. Ak sa poloha bodu 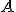 zmení, tak sa automaticky zmení aj
príslušné polia tabuľky
zmení, tak sa automaticky zmení aj
príslušné polia tabuľky 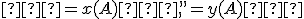 . Analogicky sa aktualizujú aj zvyšné polia tabuľky. Dynamické vstupy nám teda umožnia aktualizovať maticu
sústavy 6 rovníc aj s pravou stranou. Je to matica typu 6×7 s rozsahom je
. Analogicky sa aktualizujú aj zvyšné polia tabuľky. Dynamické vstupy nám teda umožnia aktualizovať maticu
sústavy 6 rovníc aj s pravou stranou. Je to matica typu 6×7 s rozsahom je 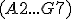 .
.
Riešenie danej sústavy 6 rovníc so 6 neznámymi s pravou stranou môžeme nájsť pomocou maticového počtu, ktorý je tiež k dispozícii v GeoGebre.
Výsledok.
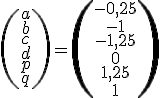
Transformačné rovnice skúmaného afinného zobrazenia sú prezentované na ďalšom obrázku v ľavej časti obrázka.
 v tomto príklade má tvar
v tomto príklade má tvar 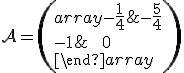 ,
čo predstavuje osovú afinitu.
,
čo predstavuje osovú afinitu.