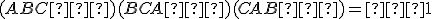Vektorový a afinný priestor
Euklidovský priestor
Deliaci pomer
Definícia (Deliaci pomer bodov).
Nech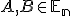 a
a 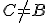 sú tri kolineárne body. Deliacim pomerom bodov
sú tri kolineárne body. Deliacim pomerom bodov 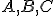 (v tomto poradí) nazývame reálne
číslo
(v tomto poradí) nazývame reálne
číslo 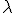 také, že
také, že 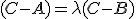 . Budeme ho označovať
. Budeme ho označovať 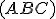 .
.
Nech
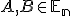 a
a 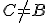 sú tri kolineárne body. Deliacim pomerom bodov
sú tri kolineárne body. Deliacim pomerom bodov 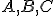 (v tomto poradí) nazývame reálne
číslo
(v tomto poradí) nazývame reálne
číslo 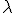 také, že
také, že 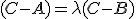 . Budeme ho označovať
. Budeme ho označovať 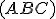 .
.
Riešenie.
-
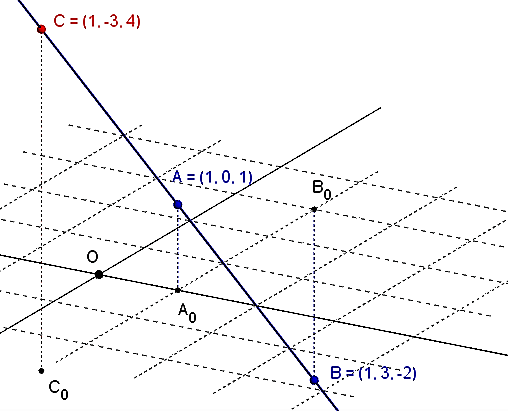
Najskôr je nutné zistiť, či body
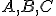 sú kolineárne.
Pre deliaci pomer
sú kolineárne.
Pre deliaci pomer 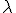 musí platiť:
musí platiť:
(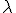 )
)
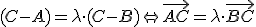 .
.
Potom môžeme spočítať
![\small \vec{u}=\overrightarrow{AC}=\left([1, -3, 4]-[1, 0, 1]\right) =(0,-3,3);\vec{v}=\overrightarrow{BC}\left([1, 3, -2]-[1, -3, 4] \right) =( 0,-6 ,6) \small \vec{u}=\overrightarrow{AC}=\left([1, -3, 4]-[1, 0, 1]\right) =(0,-3,3);\vec{v}=\overrightarrow{BC}\left([1, 3, -2]-[1, -3, 4] \right) =( 0,-6 ,6)](https://lms.umb.sk/filter/tex/pix.php/e5c9cd04bb4e1e22d826351c2a22f340.png) .
.
Po dosadení do vzťahu (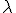 ) dostaneme
) dostaneme 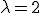 .
. - Najskôr určte súradnice priesečníka
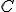 priamky
priamky 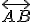 a roviny
a roviny 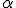 . Rovnica
priamky
. Rovnica
priamky 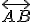 je daná parametricky
je daná parametricky
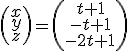
Po dosadení do všeobecnej rovnice roviny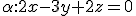 určíme riešenie
určíme riešenie 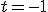 . Spoločný bod
. Spoločný bod 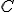 má súradnice
má súradnice ![\small [0,2,3] \small [0,2,3]](https://lms.umb.sk/filter/tex/pix.php/632489b694fb563d57a0e3ea6a4d43c4.png) .
.
- Najskôr určte súradnice bodov
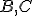 .
.
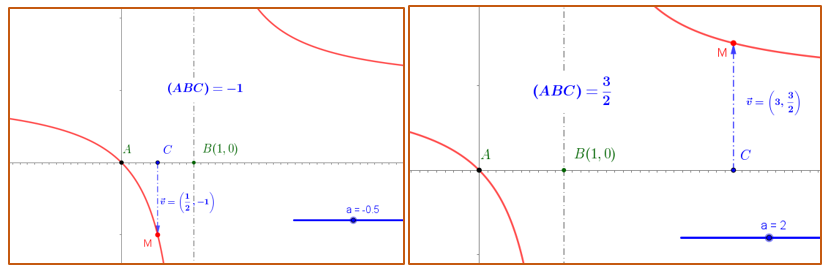
Nasledujúce obrázky dokumentujú vzťah deliaceho pomeru pre pevne zvolené body 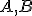 a premenlivý bod
a premenlivý bod 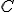 . Tento vzťah predstavuje hyperbolickú funkciu.
. Tento vzťah predstavuje hyperbolickú funkciu.
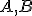 a premenlivý bod
a premenlivý bod 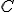 . Tento vzťah predstavuje hyperbolickú funkciu.
. Tento vzťah predstavuje hyperbolickú funkciu.
Tvrdenie (Vzťah deliaceho pomeru a lineárnej kombinácie).
Nech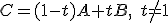 . Potom pre deliaci pomer platí:
. Potom pre deliaci pomer platí:
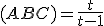 . Pozrite si grafické zdôvodnenie
Tu.
. Pozrite si grafické zdôvodnenie
Tu.
Nech
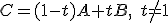 . Potom pre deliaci pomer platí:
. Potom pre deliaci pomer platí:
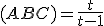 . Pozrite si grafické zdôvodnenie
Tu.
. Pozrite si grafické zdôvodnenie
Tu.
Poznámky.
- Z definície deliaceho pomeru
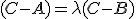 vyplýva, že vektory
vyplýva, že vektory 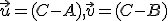 sú lineárne závislé a
platí
sú lineárne závislé a
platí 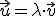 . Preto kvôli korektnosti definície deliaceho pomeru je v definícii uvádzaná podmienka kolineárnosti bodov
. Preto kvôli korektnosti definície deliaceho pomeru je v definícii uvádzaná podmienka kolineárnosti bodov 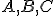 . Z predchádzajúceho tvrdenia aj z cvičenia 3. tiež vyplýva, že body
. Z predchádzajúceho tvrdenia aj z cvičenia 3. tiež vyplýva, že body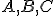 sú kolineárne.
sú kolineárne. - Z cvičenia 1. vyplýva, že existuje bod
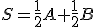 , ktorý budeme nazývať stred dvojice bodov
, ktorý budeme nazývať stred dvojice bodov  (resp. úsečky
(resp. úsečky 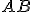 ). Ak
). Ak 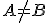 , tak pre stred
, tak pre stred  platí
platí 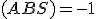 .
Stred dvojice bodov
.
Stred dvojice bodov  budeme označovat’
budeme označovat’ 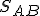 .
.
Tvrdenie.
a) Nech body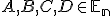 , potom vektory
, potom vektory 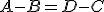 (sa rovnajú) práve vtedy, keď
(sa rovnajú) práve vtedy, keď 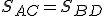 (stred rovnobežníka).
(stred rovnobežníka).
b) Pre súradnice stredu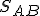 platí:
platí: 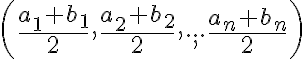 .
.
Výberové témy a) Nech body
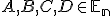 , potom vektory
, potom vektory 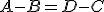 (sa rovnajú) práve vtedy, keď
(sa rovnajú) práve vtedy, keď 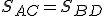 (stred rovnobežníka).
(stred rovnobežníka).
b) Pre súradnice stredu
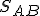 platí:
platí: 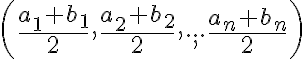 .
.
Tvrdenie (Menelaos).
Nech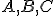 sú nekolineárne body a nech
sú nekolineárne body a nech 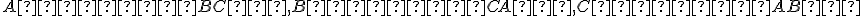 sú body rôzne od bodov
sú body rôzne od bodov 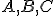 . Potom
body
. Potom
body 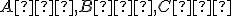 sú kolineárne práve vtedy, keď
sú kolineárne práve vtedy, keď 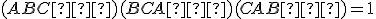 .
.
Nech
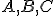 sú nekolineárne body a nech
sú nekolineárne body a nech 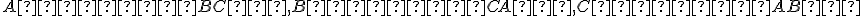 sú body rôzne od bodov
sú body rôzne od bodov 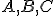 . Potom
body
. Potom
body 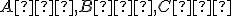 sú kolineárne práve vtedy, keď
sú kolineárne práve vtedy, keď 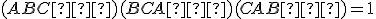 .
.
Dôkaz.
Zvoľme afinnú sústavu súradníc tak, že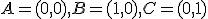 . Body
. Body 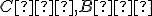 majú po rade súradnice
majú po rade súradnice 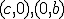 ,
pričom
,
pričom 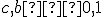 . Rovnica nadroviny (priamky)
. Rovnica nadroviny (priamky) 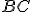 má všeobecnú rovnicu
má všeobecnú rovnicu 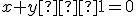 . Preto
. Preto 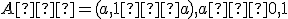 .
Z definície deliaceho pomeru dostaneme
.
Z definície deliaceho pomeru dostaneme
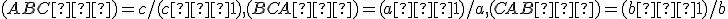 .
.
Po jednoduchých úpravách ľahko zistíme, že rovnosť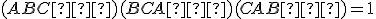 je ekvivalentná s rovnosťou
je ekvivalentná s rovnosťou 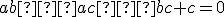 .
.
Na druhej strane body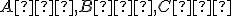 sú kolineárne práve vtedy, keď ležia na jednej priamke. Priamka určená bodmi
sú kolineárne práve vtedy, keď ležia na jednej priamke. Priamka určená bodmi 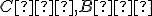 má parametrické vyjadrenie
má parametrické vyjadrenie
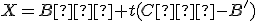 .
.
Bod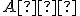 leží na tejto priamke práve vtedy, keď platí
leží na tejto priamke práve vtedy, keď platí 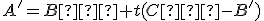 . Po dosadení súradníc dostaneme sústavu dvoch rovníc o jednej neznámej
. Po dosadení súradníc dostaneme sústavu dvoch rovníc o jednej neznámej 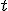 ,
ktorá má riešenie práve vtedy, keď platí
,
ktorá má riešenie práve vtedy, keď platí 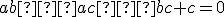 .
.
Zvoľme afinnú sústavu súradníc tak, že
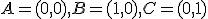 . Body
. Body 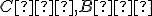 majú po rade súradnice
majú po rade súradnice 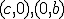 ,
pričom
,
pričom 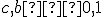 . Rovnica nadroviny (priamky)
. Rovnica nadroviny (priamky) 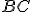 má všeobecnú rovnicu
má všeobecnú rovnicu 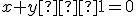 . Preto
. Preto 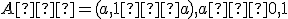 .
Z definície deliaceho pomeru dostaneme
.
Z definície deliaceho pomeru dostaneme
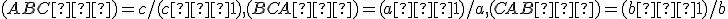 .
.
Po jednoduchých úpravách ľahko zistíme, že rovnosť
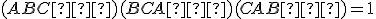 je ekvivalentná s rovnosťou
je ekvivalentná s rovnosťou 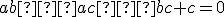 .
.
Na druhej strane body
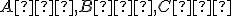 sú kolineárne práve vtedy, keď ležia na jednej priamke. Priamka určená bodmi
sú kolineárne práve vtedy, keď ležia na jednej priamke. Priamka určená bodmi 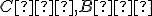 má parametrické vyjadrenie
má parametrické vyjadrenie
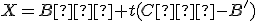 .
.
Bod
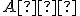 leží na tejto priamke práve vtedy, keď platí
leží na tejto priamke práve vtedy, keď platí 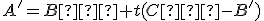 . Po dosadení súradníc dostaneme sústavu dvoch rovníc o jednej neznámej
. Po dosadení súradníc dostaneme sústavu dvoch rovníc o jednej neznámej 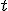 ,
ktorá má riešenie práve vtedy, keď platí
,
ktorá má riešenie práve vtedy, keď platí 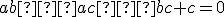 .
.
![\small A = [1, 0, 1], B = [1, 3, -2], C = [1, -3, 4] \small A = [1, 0, 1], B = [1, 3, -2], C = [1, -3, 4]](https://lms.umb.sk/filter/tex/pix.php/9357e6163937d339ddb9873c6f64ea12.png)
![\small A = [1, 1, 1], B = [2, 0, -1], C = AB \cap \alpha , \alpha : 2x -3y + 2z = 0 \small A = [1, 1, 1], B = [2, 0, -1], C = AB \cap \alpha , \alpha : 2x -3y + 2z = 0](https://lms.umb.sk/filter/tex/pix.php/3fe1a88879f544bf32fac05aaf94bcc7.png)
![\small A = [1, -1], B = A + 2\vec u, C = A- \vec u, \vec u = (1, 2). \small A = [1, -1], B = A + 2\vec u, C = A- \vec u, \vec u = (1, 2).](https://lms.umb.sk/filter/tex/pix.php/982c567b39f78a847677a6718229ff13.png)