Vektorový a afinný priestor
Analytické vyjadrenie
Vzor a obraz
Nech je dané afinné zobrazenie  , v ktorom sa súradný repér zobrazí na repér
, v ktorom sa súradný repér zobrazí na repér 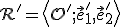 .
V tejto kapitole sa budeme zaoberať
.
V tejto kapitole sa budeme zaoberať
 , v ktorom sa súradný repér zobrazí na repér
, v ktorom sa súradný repér zobrazí na repér 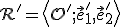 .
V tejto kapitole sa budeme zaoberať
.
V tejto kapitole sa budeme zaoberať
- obrazom bodu v afinnom zobrazení
- obrazom priamky v afinnom zobrazení
- hľadaním vzoru k obrazu bodu
Poznámky.
- Obraz ľubovoľného bodu
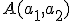 v afinnom zobrazení
v afinnom zobrazení  určíme jednoducho tak, že súradnice tohto bodu dosadíme do transformačných rovníc.
Dostaneme rovnosti
určíme jednoducho tak, že súradnice tohto bodu dosadíme do transformačných rovníc.
Dostaneme rovnosti 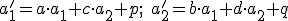 , pričom čísla
, pričom čísla 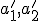 predstavujú súradnice bodu
predstavujú súradnice bodu 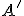 .
. - Určiť obraz priamky
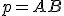 v afinnom zobrazení znamená určiť rovnicu priamky
v afinnom zobrazení znamená určiť rovnicu priamky 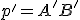 . To môžeme urobiť dvoma spôsobmi.
. To môžeme urobiť dvoma spôsobmi.
- Ak priamka
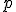 je určená dvomi rôznymi bodmi
je určená dvomi rôznymi bodmi  , tak súradnice bodov
, tak súradnice bodov  dosadíme do transformačných rovníc
afinného zobrazenia. Výpočtom popísanom v predchádzajúcom odseku určíme súradnice bodov
dosadíme do transformačných rovníc
afinného zobrazenia. Výpočtom popísanom v predchádzajúcom odseku určíme súradnice bodov 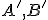 , ktorými bude určená priamka
, ktorými bude určená priamka 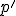 .
Potom určíme napríklad parametrické rovnice priamky
.
Potom určíme napríklad parametrické rovnice priamky 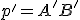 .
. - Ak priamka
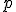 je určená rovnicou (napr. vo všeobecnom tvare
je určená rovnicou (napr. vo všeobecnom tvare 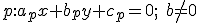 ), tak do transformačných rovníc
), tak do transformačných rovníc
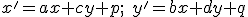 dosadíme za premenné
dosadíme za premenné 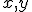 súradnice všeobecného bodu
súradnice všeobecného bodu 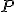 priamky. Tento bod určíme pomocou parametra
priamky. Tento bod určíme pomocou parametra 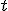 v tvare
v tvare ![\small P[t,- \frac{at+c}{b}] \small P[t,- \frac{at+c}{b}]](https://lms.umb.sk/filter/tex/pix.php/29afefab61a72fec5c2f84dc7dc259dc.png) .
(V prípade. že
.
(V prípade. že 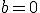 zvolíme parameter
zvolíme parameter 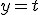 ). Po dosadení dostaneme parametrické
rovnice obrazu priamky
). Po dosadení dostaneme parametrické
rovnice obrazu priamky
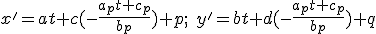 .
.
- Ak priamka
- Nájsť vzor
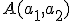 k danému obrazu
k danému obrazu 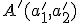 v afinnom zobrazení
v afinnom zobrazení  určíme tak, že súradnice obrazu bodu
určíme tak, že súradnice obrazu bodu 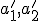 dosadíme do transformačných rovníc za premenné
dosadíme do transformačných rovníc za premenné 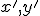 . Dostaneme sústavu dvoch rovních o neznámych
. Dostaneme sústavu dvoch rovních o neznámych 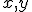 . Riešenie tejto súsatavy predstavuje
súradnice hľadaného vzoru.
. Riešenie tejto súsatavy predstavuje
súradnice hľadaného vzoru.
Riešenie
Analytické riešenie: Transformačné rovnice sú
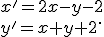
Analytické riešenie: Transformačné rovnice sú
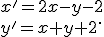
- Pre priamku
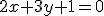 má jej ľubovoľný bod
má jej ľubovoľný bod 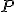 súradnice
súradnice ![\small P[t,- \frac{2t+1}{3}] \small P[t,- \frac{2t+1}{3}]](https://lms.umb.sk/filter/tex/pix.php/925952d4a088ed38baaffc731c9eb649.png) Po dosadení do transformačných rovníc
dostaneme sústavu parametrických rovníc
Po dosadení do transformačných rovníc
dostaneme sústavu parametrických rovníc
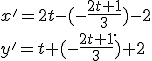
Výsledok: po úprave na všeobecný tvar dostaneme rovnicu obrazu priamky: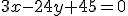
Na syntetické riešenie použite applet Tu. - Keďže každý bod priamky \small x=1 \) má prvú súradnicu rovnú 1, tak stačí hodnotu \small x=1 \) dosadiť do transformačných rovníc a dostaneme rovnice
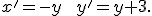 Po dosadení do druhej rovnice
Po dosadení do druhej rovnice 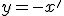 dostaneme rovnicu obrazu priamky
dostaneme rovnicu obrazu priamky 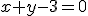 .
.
Príklad.
Dané je afinné zobrazenie transformačnými rovnicami
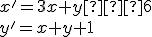 .
.
Ktoré body sa zobrazia do bodov [9, 8] a [−6, 1]?
Dané je afinné zobrazenie transformačnými rovnicami
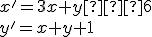 .
.
Ktoré body sa zobrazia do bodov [9, 8] a [−6, 1]?
Riešenie
Súradnice bodu [9, 8] dosadíme do transformačných rovníc za premenné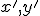 . Riešením je dvojica
. Riešením je dvojica 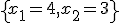 . Otvorte si applet na riešenie rovníc Tu.
. Otvorte si applet na riešenie rovníc Tu.
Súradnice bodu [9, 8] dosadíme do transformačných rovníc za premenné
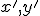 . Riešením je dvojica
. Riešením je dvojica 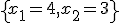 . Otvorte si applet na riešenie rovníc Tu.
. Otvorte si applet na riešenie rovníc Tu.![\small \mathcal R' = \left \langle O'=[ \frac{-1-\sqrt{3}}{2} , \frac{-1+\sqrt{3}}{2}]; \vec e'_1=( \frac{1}{2},-\frac{\sqrt{3}}{2} ), \vec e'_2=(\frac{\sqrt{3}}{2},\frac{1}{2}) \right\rangle \small \mathcal R' = \left \langle O'=[ \frac{-1-\sqrt{3}}{2} , \frac{-1+\sqrt{3}}{2}]; \vec e'_1=( \frac{1}{2},-\frac{\sqrt{3}}{2} ), \vec e'_2=(\frac{\sqrt{3}}{2},\frac{1}{2}) \right\rangle](https://lms.umb.sk/filter/tex/pix.php/e2cdc039ed14408daf8c2b2514abac14.png)
![\small [-1,1], [-1,-1] \small [-1,1], [-1,-1]](https://lms.umb.sk/filter/tex/pix.php/53e28ab8a315deb4586b9442a406b896.png)
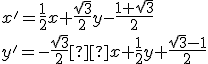
![\small [-1,1] \small [-1,1]](https://lms.umb.sk/filter/tex/pix.php/c0b0c9cea429ed1994542f478aba8817.png)
![\small \mathcal R' = \left \langle O'=[ -2 , 2]; \vec e'_1=(2,1), \vec e'_2=(-1,1) \right\rangle \small \mathcal R' = \left \langle O'=[ -2 , 2]; \vec e'_1=(2,1), \vec e'_2=(-1,1) \right\rangle](https://lms.umb.sk/filter/tex/pix.php/31f70cf40d8c1a8eebff87571542c457.png)