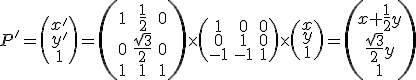Vektorový a afinný priestor
Analytické vyjadrenie
Obraz repéra
Z analytického vyjadrenia afinného zobrazenia 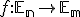 vyplýva, že takéto afinné zobrazenie je jednoznačne určené, ak poznáme obraz
vyplýva, že takéto afinné zobrazenie je jednoznačne určené, ak poznáme obraz 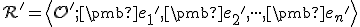 súradného repéru
súradného repéru 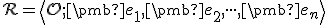 v tomto zobrazení. Analytické vyjadrenie daného zobrazenia je určené vzťahom (AV) v kapitole "Analytické vyjadrenie".
v tomto zobrazení. Analytické vyjadrenie daného zobrazenia je určené vzťahom (AV) v kapitole "Analytické vyjadrenie".
V tejto kapitole sa budeme zaoberať transformáciami euklidovskej roviny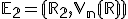 , ktorá má repér
, ktorá má repér
![\small \mathcal R =\left\langle O[0,0];\pmb {e_1}=(1,0),\pmb {e_2}=(0,1)\right\rangle \small \mathcal R =\left\langle O[0,0];\pmb {e_1}=(1,0),\pmb {e_2}=(0,1)\right\rangle](https://lms.umb.sk/filter/tex/pix.php/2831d609507dca97ba6f6635794431e6.png) . Nech tento súradný repér v afinnom zobrazení
. Nech tento súradný repér v afinnom zobrazení  sa zobrazí na repér
sa zobrazí na repér
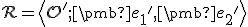 . Vektory
. Vektory 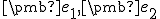 sú lineárne nezávislé, preto aj ich obrazy
sú lineárne nezávislé, preto aj ich obrazy 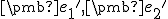 sú zrejme lineárne nezávislé. Dokážte to!
sú zrejme lineárne nezávislé. Dokážte to!
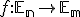 vyplýva, že takéto afinné zobrazenie je jednoznačne určené, ak poznáme obraz
vyplýva, že takéto afinné zobrazenie je jednoznačne určené, ak poznáme obraz 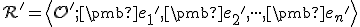 súradného repéru
súradného repéru 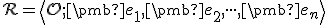 v tomto zobrazení. Analytické vyjadrenie daného zobrazenia je určené vzťahom (AV) v kapitole "Analytické vyjadrenie".
v tomto zobrazení. Analytické vyjadrenie daného zobrazenia je určené vzťahom (AV) v kapitole "Analytické vyjadrenie".
V tejto kapitole sa budeme zaoberať transformáciami euklidovskej roviny
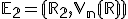 , ktorá má repér
, ktorá má repér
![\small \mathcal R =\left\langle O[0,0];\pmb {e_1}=(1,0),\pmb {e_2}=(0,1)\right\rangle \small \mathcal R =\left\langle O[0,0];\pmb {e_1}=(1,0),\pmb {e_2}=(0,1)\right\rangle](https://lms.umb.sk/filter/tex/pix.php/2831d609507dca97ba6f6635794431e6.png) . Nech tento súradný repér v afinnom zobrazení
. Nech tento súradný repér v afinnom zobrazení  sa zobrazí na repér
sa zobrazí na repér
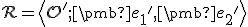 . Vektory
. Vektory 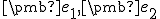 sú lineárne nezávislé, preto aj ich obrazy
sú lineárne nezávislé, preto aj ich obrazy 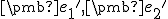 sú zrejme lineárne nezávislé. Dokážte to!
sú zrejme lineárne nezávislé. Dokážte to!
Maticový zápis pre rovinné afinné zobrazenie 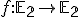 určené obrazom repéra
určené obrazom repéra 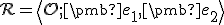 bude mať nasledovný tvar
bude mať nasledovný tvar
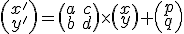 alebo
alebo
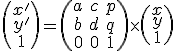 ,
,
kde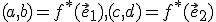 sú obrazy súradnicových vektorov v asociovanom zobrazení
sú obrazy súradnicových vektorov v asociovanom zobrazení 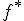 a
a ![\small [p,q]=f(O) \small [p,q]=f(O)](https://lms.umb.sk/filter/tex/pix.php/feb3f3a5de864768600e9bca42c058f3.png) je obraz začiatku súradnej sústavy v afinnom zobrazení
je obraz začiatku súradnej sústavy v afinnom zobrazení 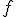 .
.
 určené obrazom repéra
určené obrazom repéra 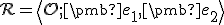 bude mať nasledovný tvar
bude mať nasledovný tvar
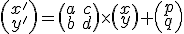 alebo
alebo
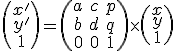 ,
,
kde
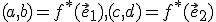 sú obrazy súradnicových vektorov v asociovanom zobrazení
sú obrazy súradnicových vektorov v asociovanom zobrazení 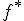 a
a ![\small [p,q]=f(O) \small [p,q]=f(O)](https://lms.umb.sk/filter/tex/pix.php/feb3f3a5de864768600e9bca42c058f3.png) je obraz začiatku súradnej sústavy v afinnom zobrazení
je obraz začiatku súradnej sústavy v afinnom zobrazení 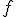 .
.
Matica  sa nazýva transformačná matica afinného zobrazenia
sa nazýva transformačná matica afinného zobrazenia 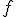 .
.
Pri určovaní afinného zobrazenia, ktoré je určené obrazom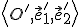 , môžeme transformačné rovnice určiť priamo pomocou súradníc obrazu počiatku
, môžeme transformačné rovnice určiť priamo pomocou súradníc obrazu počiatku 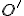 a súradníc vektorov
a súradníc vektorov 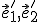 . Súradnice obrazu ľubovoľného bodu
. Súradnice obrazu ľubovoľného bodu  roviny potom môžeme získať tak, že do transformačných rovníc dosadíme súradnice
bodu
roviny potom môžeme získať tak, že do transformačných rovníc dosadíme súradnice
bodu ![\small P[x_p, y_p] \small P[x_p, y_p]](https://lms.umb.sk/filter/tex/pix.php/f7bff613390be76a0f1fa7b64a9da5b3.png) .
.
 sa nazýva transformačná matica afinného zobrazenia
sa nazýva transformačná matica afinného zobrazenia 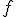 .
.
Pri určovaní afinného zobrazenia, ktoré je určené obrazom
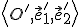 , môžeme transformačné rovnice určiť priamo pomocou súradníc obrazu počiatku
, môžeme transformačné rovnice určiť priamo pomocou súradníc obrazu počiatku 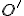 a súradníc vektorov
a súradníc vektorov 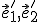 . Súradnice obrazu ľubovoľného bodu
. Súradnice obrazu ľubovoľného bodu  roviny potom môžeme získať tak, že do transformačných rovníc dosadíme súradnice
bodu
roviny potom môžeme získať tak, že do transformačných rovníc dosadíme súradnice
bodu ![\small P[x_p, y_p] \small P[x_p, y_p]](https://lms.umb.sk/filter/tex/pix.php/f7bff613390be76a0f1fa7b64a9da5b3.png) .
.
Príklad - obraz bodu  a kružnice euklidovskej roviny.
a kružnice euklidovskej roviny.
 a kružnice euklidovskej roviny.
a kružnice euklidovskej roviny.
-
Určte transformačné rovnice afinného zobrazenia, ktoré postupne zobrazuje body súradného repéra
![\small O=[0, 0], E_1=[1, 0],E_2=[0, 1] \small O=[0, 0], E_1=[1, 0],E_2=[0, 1]](https://lms.umb.sk/filter/tex/pix.php/56ce3f57c162b4eb54eff0ef324ee891.png) do bodov
do bodov
![\small O'=O[0, 0], E_1'=E_1[1, 0], E_2'=[\frac{1}{2},\frac{\sqrt{3}}{2}] \small O'=O[0, 0], E_1'=E_1[1, 0], E_2'=[\frac{1}{2},\frac{\sqrt{3}}{2}]](https://lms.umb.sk/filter/tex/pix.php/e4851d242d578efca580e2dc281bee93.png) v tomto poradí.
v tomto poradí. - Určte obraz ľubovoľného bodu
![\small P[x_p, y_p] \small P[x_p, y_p]](https://lms.umb.sk/filter/tex/pix.php/f7bff613390be76a0f1fa7b64a9da5b3.png) .
. - Určte obraz kružnice
![\small k(S=[0, 0],r=3) \small k(S=[0, 0],r=3)](https://lms.umb.sk/filter/tex/pix.php/4af7ad0874964396095d6e079d2d64e7.png) pomocou nástroja "Množina bodov".
pomocou nástroja "Množina bodov". - Pokúste sa toto afinné zobrazenie geometricky interpretovať. Príklad je prevzatý z práce (Chalmoviansky, Cvičenie 29).
Riešenie.
- Najskôr musíme určiť obraz súradného repéra
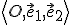 . Keďže začiatok súradnej sústavy bod
. Keďže začiatok súradnej sústavy bod ![\small O=O'[0, 0] \small O=O'[0, 0]](https://lms.umb.sk/filter/tex/pix.php/3e365e95cef0de0e28fa7bc6aefcd085.png) je samodružný, tak pre obrazy vektorov
je samodružný, tak pre obrazy vektorov 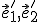 bude platiť
bude platiť 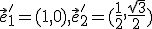 .
Transformačné rovnice určíme dosadením súradníc obrazov vektorov
.
Transformačné rovnice určíme dosadením súradníc obrazov vektorov 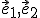
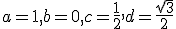
a súradníc bodu![\small O'[p=0, q=0] \small O'[p=0, q=0]](https://lms.umb.sk/filter/tex/pix.php/3157dd0faaba26df499fd924dc638db3.png) do sústavy dvoch lineárnych rovníc o dvoch neznámych
do sústavy dvoch lineárnych rovníc o dvoch neznámych
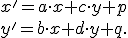
Dostaneme transformačné rovnice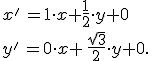
- Súradnice obrazu ľubovoľného bodu
 určíme dosadením jeho súradníc
určíme dosadením jeho súradníc 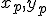 do transformačných rovníc. Pre súradnice
do transformačných rovníc. Pre súradnice
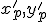 dostaneme
dostaneme
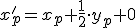
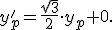
Výsledok napríklad pre bod![\small P[-2, 3] \small P[-2, 3]](https://lms.umb.sk/filter/tex/pix.php/510391cd5be21da625dd57b7daa77115.png) je
je ![\small P'\left [-\frac{1}{2}, \frac{3 \sqrt(3)}{2} \right ] \small P'\left [-\frac{1}{2}, \frac{3 \sqrt(3)}{2} \right ]](https://lms.umb.sk/filter/tex/pix.php/a5ce5c70f8eb8eb57367fa0a12072ec2.png) .
. - Samostatná práca: V GeoGebra applete (upravte applet "Kompletné grafické riešenie ..." z príkladu Tri body) si zvoľte si ľubovoľnú kružnicu
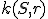 a na nej si zvoľte ľubovoľný "Bod na objekte"
a na nej si zvoľte ľubovoľný "Bod na objekte"  .
Potom vo vlastnostiach bodu
.
Potom vo vlastnostiach bodu  v definícii zadajte P=L. Nakoniec aktivujte nástroj "Množina bodov" a kliknite postupne na bod
v definícii zadajte P=L. Nakoniec aktivujte nástroj "Množina bodov" a kliknite postupne na bod
 a potom na bod
a potom na bod  .
.
- Na základe obrazu kružnice ide o osovú afinitu, ktorej os je x-ová súradná os. Ukážte, že každý bod x-ovej súradnej osi je samodružný.
- Kompletná konštrukcia - "Dynamický repér" Tu.