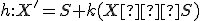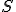Vektorový a afinný priestor
Analytické vyjadrenie
Nech je v 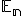 je afinné zobrazenie
je afinné zobrazenie  , v ktorom sa repér
, v ktorom sa repér 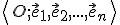 zobrazí na repér
zobrazí na repér 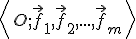 , pričom pre súradnice obrazov platí
, pričom pre súradnice obrazov platí
![\small f(O)=[r_1,r_2,...,r_m] \small f(O)=[r_1,r_2,...,r_m]](https://lms.umb.sk/filter/tex/pix.php/c5eda1f88fc333cd5842ee547a31e19d.png)
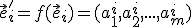 .
.
Nech![\small X=[x_1,x_2,...,x_n] \small X=[x_1,x_2,...,x_n]](https://lms.umb.sk/filter/tex/pix.php/a5dcae89eca8a64e02819035d3279438.png) je bod euklidovského priestoru, potom pre jeho obraz
je bod euklidovského priestoru, potom pre jeho obraz ![\small X'=[x'_1,x'_2,...,x'_m] \small X'=[x'_1,x'_2,...,x'_m]](https://lms.umb.sk/filter/tex/pix.php/6ab3a2d90723d2e20d5aa14c22d84357.png) bude platiť
bude platiť
(AV)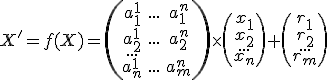 .
.
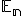 je afinné zobrazenie
je afinné zobrazenie  , v ktorom sa repér
, v ktorom sa repér 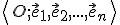 zobrazí na repér
zobrazí na repér 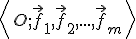 , pričom pre súradnice obrazov platí
, pričom pre súradnice obrazov platí
![\small f(O)=[r_1,r_2,...,r_m] \small f(O)=[r_1,r_2,...,r_m]](https://lms.umb.sk/filter/tex/pix.php/c5eda1f88fc333cd5842ee547a31e19d.png)
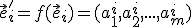 .
.
Nech
![\small X=[x_1,x_2,...,x_n] \small X=[x_1,x_2,...,x_n]](https://lms.umb.sk/filter/tex/pix.php/a5dcae89eca8a64e02819035d3279438.png) je bod euklidovského priestoru, potom pre jeho obraz
je bod euklidovského priestoru, potom pre jeho obraz ![\small X'=[x'_1,x'_2,...,x'_m] \small X'=[x'_1,x'_2,...,x'_m]](https://lms.umb.sk/filter/tex/pix.php/6ab3a2d90723d2e20d5aa14c22d84357.png) bude platiť
bude platiť
(AV)
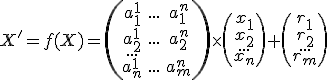 .
.
Zápis (AV) nazývame analytické vyjadrenie afinného zobrazenia 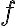 vzhľadom k afinnej súradnicovej sústave
vzhľadom k afinnej súradnicovej sústave
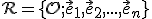 .
.
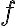 vzhľadom k afinnej súradnicovej sústave
vzhľadom k afinnej súradnicovej sústave
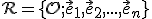 .
.
Namiesto označenia 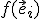 budeme tiež používať označenie
budeme tiež používať označenie
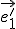 . V ďalších kapitolách sa zameriame na afinné zobrazenia v euklidovskej rovine,
pričom upriamime pozornosť na analytické vyjadrenia zhodných (zhodnostných) zobrazení v rovine.
. V ďalších kapitolách sa zameriame na afinné zobrazenia v euklidovskej rovine,
pričom upriamime pozornosť na analytické vyjadrenia zhodných (zhodnostných) zobrazení v rovine.
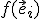 budeme tiež používať označenie
budeme tiež používať označenie
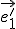 . V ďalších kapitolách sa zameriame na afinné zobrazenia v euklidovskej rovine,
pričom upriamime pozornosť na analytické vyjadrenia zhodných (zhodnostných) zobrazení v rovine.
. V ďalších kapitolách sa zameriame na afinné zobrazenia v euklidovskej rovine,
pričom upriamime pozornosť na analytické vyjadrenia zhodných (zhodnostných) zobrazení v rovine.
Úlohy.
Riešenie úlohy č. 1.
Pre identitu platí, že každý bod roviny sa zobrazí sám na seba, t. j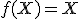 . Označme súradnice vzoru
. Označme súradnice vzoru 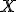 ako usporiadanú dvojicu
ako usporiadanú dvojicu 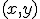 a
súradnice jeho obrazu
a
súradnice jeho obrazu 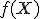 v zobrazení
v zobrazení  ako
ako 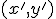 . Keďže ide o identické zobrazenie, tak musí platiť
. Keďže ide o identické zobrazenie, tak musí platiť
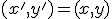 .
.
Rovnosť usporiadaných dvojíc nastane práve vtedy, keď sa rovnajú odpovedajúce zložky. Teda, keď súčasne platia rovnosti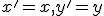 .
.
Táto jednoduchá sústava dvoch rovníc je analytickým vyjadrením identity. Ak zapíšeme získanú sústavu dvoch rovníc v maticovom tvare, tak získame rovnicu v tvare
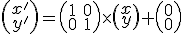
alebo v riadkovom zápise (maticou násobíme sprava!)
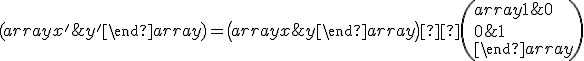 .
.
Určte analytické vyjadrenie identického zobrazenia euklidovského priestoru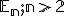 .
.
Riešenie úlohy č. 2 je v nasledujúcej kapitole.
Pre identitu platí, že každý bod roviny sa zobrazí sám na seba, t. j
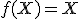 . Označme súradnice vzoru
. Označme súradnice vzoru 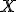 ako usporiadanú dvojicu
ako usporiadanú dvojicu 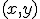 a
súradnice jeho obrazu
a
súradnice jeho obrazu 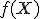 v zobrazení
v zobrazení  ako
ako 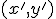 . Keďže ide o identické zobrazenie, tak musí platiť
. Keďže ide o identické zobrazenie, tak musí platiť
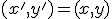 .
.
Rovnosť usporiadaných dvojíc nastane práve vtedy, keď sa rovnajú odpovedajúce zložky. Teda, keď súčasne platia rovnosti
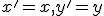 .
.
Táto jednoduchá sústava dvoch rovníc je analytickým vyjadrením identity. Ak zapíšeme získanú sústavu dvoch rovníc v maticovom tvare, tak získame rovnicu v tvare
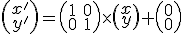
alebo v riadkovom zápise (maticou násobíme sprava!)
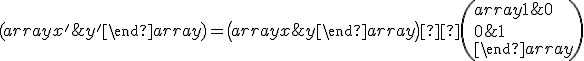 .
.
Určte analytické vyjadrenie identického zobrazenia euklidovského priestoru
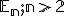 .
.
Riešenie úlohy č. 2 je v nasledujúcej kapitole.
Rozšírené afinné súradnice.
Pri riešení príkladu "Tri body" sme použili matice, ktorých posledné riadky korešpondovali s podmienkou lineárnej kombinácie bodov: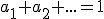 . V dôsledku tohto príkladu sme
vlastne použili rozšírené afinné súradnice, pomocou ktorých možno zjednodušiť zápis analytické vyjadrenie afinného zobrazenia. Rozšírené afinné súradnice sprehľadnia zápis zobrazení. Súradnice bodu
. V dôsledku tohto príkladu sme
vlastne použili rozšírené afinné súradnice, pomocou ktorých možno zjednodušiť zápis analytické vyjadrenie afinného zobrazenia. Rozšírené afinné súradnice sprehľadnia zápis zobrazení. Súradnice bodu ![\small X = [x_1 , . . . , x_n ] \small X = [x_1 , . . . , x_n ]](https://lms.umb.sk/filter/tex/pix.php/1d6bb0fe4aa343a6996a595b0930f987.png) nahradíme súradnicami
nahradíme súradnicami ![\small [ x_1 , . . . , x_n,1 ] \small [ x_1 , . . . , x_n,1 ]](https://lms.umb.sk/filter/tex/pix.php/a2baa221eb1ab835da5a2af8b84374ee.png) a súradnice
vektora
a súradnice
vektora 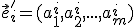 nahradíme súradnicami
nahradíme súradnicami 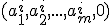 .
Pre takto zavedené rozšírenie platí obvyklá aritmetika s bodmi a vektormi z euklidovských priestorov, ako aj počítanie s lineárnymi kombináciami.
.
Pre takto zavedené rozšírenie platí obvyklá aritmetika s bodmi a vektormi z euklidovských priestorov, ako aj počítanie s lineárnymi kombináciami.
V rozšírených afinných súradniciach možno potom písať analytické vyjadrenie zobrazenia takto
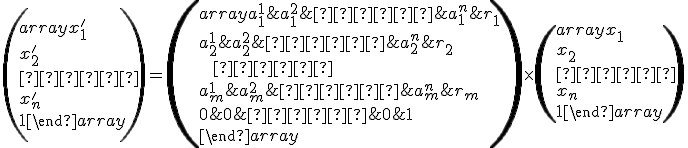 ,
,
pričom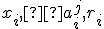 má ten istý význam ako pri afinných súradniciach.
má ten istý význam ako pri afinných súradniciach.
Pri riešení príkladu "Tri body" sme použili matice, ktorých posledné riadky korešpondovali s podmienkou lineárnej kombinácie bodov:
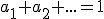 . V dôsledku tohto príkladu sme
vlastne použili rozšírené afinné súradnice, pomocou ktorých možno zjednodušiť zápis analytické vyjadrenie afinného zobrazenia. Rozšírené afinné súradnice sprehľadnia zápis zobrazení. Súradnice bodu
. V dôsledku tohto príkladu sme
vlastne použili rozšírené afinné súradnice, pomocou ktorých možno zjednodušiť zápis analytické vyjadrenie afinného zobrazenia. Rozšírené afinné súradnice sprehľadnia zápis zobrazení. Súradnice bodu ![\small X = [x_1 , . . . , x_n ] \small X = [x_1 , . . . , x_n ]](https://lms.umb.sk/filter/tex/pix.php/1d6bb0fe4aa343a6996a595b0930f987.png) nahradíme súradnicami
nahradíme súradnicami ![\small [ x_1 , . . . , x_n,1 ] \small [ x_1 , . . . , x_n,1 ]](https://lms.umb.sk/filter/tex/pix.php/a2baa221eb1ab835da5a2af8b84374ee.png) a súradnice
vektora
a súradnice
vektora 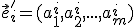 nahradíme súradnicami
nahradíme súradnicami 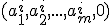 .
Pre takto zavedené rozšírenie platí obvyklá aritmetika s bodmi a vektormi z euklidovských priestorov, ako aj počítanie s lineárnymi kombináciami.
.
Pre takto zavedené rozšírenie platí obvyklá aritmetika s bodmi a vektormi z euklidovských priestorov, ako aj počítanie s lineárnymi kombináciami.
V rozšírených afinných súradniciach možno potom písať analytické vyjadrenie zobrazenia takto
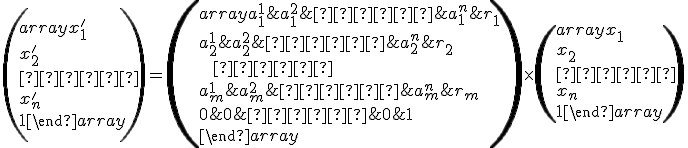 ,
,
pričom
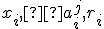 má ten istý význam ako pri afinných súradniciach.
má ten istý význam ako pri afinných súradniciach.