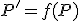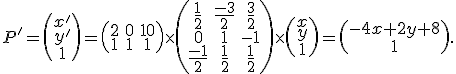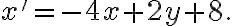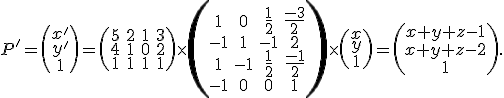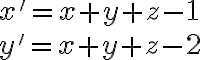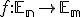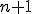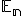Vektorový a afinný priestor
Afinné zobrazenie
Rôzne dimanzie
V predchádzajúcej kapitole sme riešili úlohy transfomácie euklidovských priestorov 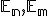 , keď
, keď 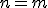 . V tejto kapitole sa budeme zaoberať prípadom
. V tejto kapitole sa budeme zaoberať prípadom 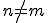 .
.
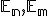 , keď
, keď 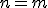 . V tejto kapitole sa budeme zaoberať prípadom
. V tejto kapitole sa budeme zaoberať prípadom 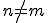 .
.
Príklad zobrazenie 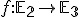 .
.
Určte parameter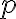 tak, aby zobrazenie ktoré zobrazuje body
tak, aby zobrazenie ktoré zobrazuje body ![\small A[1, 0], B[0, 1],C[2, p] \small A[1, 0], B[0, 1],C[2, p]](https://lms.umb.sk/filter/tex/pix.php/f49c0b3f0bf1453ab07e57c5c4d6e0d0.png) do bodov
do bodov ![\small A'[2,1,-1], B'[3,2,0], C'[1,0,2] \small A'[2,1,-1], B'[3,2,0], C'[1,0,2]](https://lms.umb.sk/filter/tex/pix.php/1fc10b7b65fbaf2986dee4ec72a5bc02.png) v tomto poradí bolo afinné. Pre vhodné
v tomto poradí bolo afinné. Pre vhodné 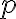 Príklad je prevzatý z práce Monoszová, 2.časť, Cvičenie 3.3.5.
Príklad je prevzatý z práce Monoszová, 2.časť, Cvičenie 3.3.5.
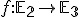 .
.
Určte parameter
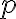 tak, aby zobrazenie ktoré zobrazuje body
tak, aby zobrazenie ktoré zobrazuje body ![\small A[1, 0], B[0, 1],C[2, p] \small A[1, 0], B[0, 1],C[2, p]](https://lms.umb.sk/filter/tex/pix.php/f49c0b3f0bf1453ab07e57c5c4d6e0d0.png) do bodov
do bodov ![\small A'[2,1,-1], B'[3,2,0], C'[1,0,2] \small A'[2,1,-1], B'[3,2,0], C'[1,0,2]](https://lms.umb.sk/filter/tex/pix.php/1fc10b7b65fbaf2986dee4ec72a5bc02.png) v tomto poradí bolo afinné. Pre vhodné
v tomto poradí bolo afinné. Pre vhodné 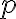 Príklad je prevzatý z práce Monoszová, 2.časť, Cvičenie 3.3.5.
Príklad je prevzatý z práce Monoszová, 2.časť, Cvičenie 3.3.5.
Riešenie.
Body![\small P[x, y];P'[x', y'] \small P[x, y];P'[x', y']](https://lms.umb.sk/filter/tex/pix.php/15c79f2a8b929f1e644ab5dcf9d0f0fa.png) vyjadrime ako lineárne kombinácie
vyjadrime ako lineárne kombinácie
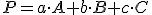
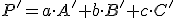 ,
,
kde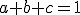 .Zápis v maticovom tvare V predchádzajúcej kapitole sme ukázali, že
.Zápis v maticovom tvare V predchádzajúcej kapitole sme ukázali, že
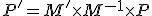 ,
,
kde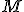 je matica vzorov,
je matica vzorov, 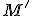 matica obrazov
matica obrazov
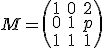 ,
,
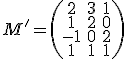 .
.
Pomocou maticovej kalkulačky určíme inverznú maticu.
Roznásobením
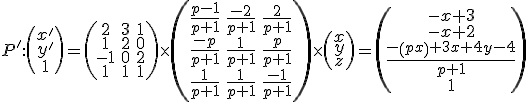 .
.
a porovaním ľavej a pravej strany dostaneme transformačné rovnice
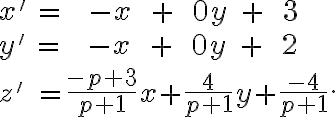
Body
![\small P[x, y];P'[x', y'] \small P[x, y];P'[x', y']](https://lms.umb.sk/filter/tex/pix.php/15c79f2a8b929f1e644ab5dcf9d0f0fa.png) vyjadrime ako lineárne kombinácie
vyjadrime ako lineárne kombinácie
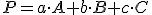
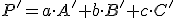 ,
,
kde
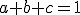 .Zápis v maticovom tvare V predchádzajúcej kapitole sme ukázali, že
.Zápis v maticovom tvare V predchádzajúcej kapitole sme ukázali, že
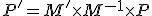 ,
,
kde
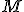 je matica vzorov,
je matica vzorov, 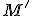 matica obrazov
matica obrazov
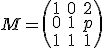 ,
,
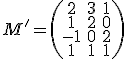 .
.
Pomocou maticovej kalkulačky určíme inverznú maticu.
Roznásobením
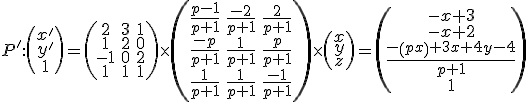 .
.
a porovaním ľavej a pravej strany dostaneme transformačné rovnice
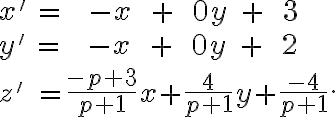
Zobrazenie bude afinným práve vtedy, ak 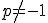 . Súradnice obrazu ľubovoľného bodu
. Súradnice obrazu ľubovoľného bodu ![\small P[x, y] \small P[x, y]](https://lms.umb.sk/filter/tex/pix.php/7e18944b1e340466fd42d0882b61be14.png) určíme dosadením súradníc
určíme dosadením súradníc 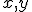 do transformačných rovníc. Napríklad pre
do transformačných rovníc. Napríklad pre ![\small D[3,1] \small D[3,1]](https://lms.umb.sk/filter/tex/pix.php/d87ae2aa6878e674fae0498a5a39d4ee.png) a
a 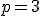 dostaneme
dostaneme ![\small D'[0,-1,0] \small D'[0,-1,0]](https://lms.umb.sk/filter/tex/pix.php/ce1572c3ffb0d63e754073ce9d707f14.png) .
.
Kružnica určená bodmi![\small A[1, 0], B[0, 1],C[2, 3] \small A[1, 0], B[0, 1],C[2, 3]](https://lms.umb.sk/filter/tex/pix.php/d68e7110804078192907e062e23a2c9c.png) má stred v bode
má stred v bode ![\small S \left [\frac{1}{2}, \frac{1}{2} \right ] \small S \left [\frac{1}{2}, \frac{1}{2} \right ]](https://lms.umb.sk/filter/tex/pix.php/1f862ef6072de16856c6272e4ef49ff7.png) a polomer
a polomer 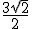 a jej parametrické vyjadrenie má tvar pozrite si prácu "Kružnica, Veta 8"
Tu)
a jej parametrické vyjadrenie má tvar pozrite si prácu "Kružnica, Veta 8"
Tu)
![\small \left [\frac{3}{2}, \frac{3}{2} \right ] +\left [\frac{3 \sqrt{2} }{2}\cos t ,\frac{3 \sqrt{2} }{2}\sin t\right ] \small \left [\frac{3}{2}, \frac{3}{2} \right ] +\left [\frac{3 \sqrt{2} }{2}\cos t ,\frac{3 \sqrt{2} }{2}\sin t\right ]](https://lms.umb.sk/filter/tex/pix.php/540ac5353a475dc3c3788ff54a224437.png) .
.
Po dosadení týchto parametrických súradníc do transformačných rovníc, zistíme, že obrazom je elipsa ležiaca v rovine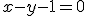 . Jej parametrické vyjadrenie má tvar
. Jej parametrické vyjadrenie má tvar
![\small \left [\frac{3}{2}, \frac{1}{2}, \frac{3}{2} \right ] +\left [-\frac{1}{2}\cos t +\frac{3}{2}\sin t,-\frac{1}{2}\cos t +\frac{3}{2}\sin t, \frac{3}{2}\cos t +\frac{1}{2}\sin t\right ], t, 0, 2π \small \left [\frac{3}{2}, \frac{1}{2}, \frac{3}{2} \right ] +\left [-\frac{1}{2}\cos t +\frac{3}{2}\sin t,-\frac{1}{2}\cos t +\frac{3}{2}\sin t, \frac{3}{2}\cos t +\frac{1}{2}\sin t\right ], t, 0, 2π](https://lms.umb.sk/filter/tex/pix.php/49c8dec70429e172c716a85f61c8fbd7.png) .
.
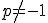 . Súradnice obrazu ľubovoľného bodu
. Súradnice obrazu ľubovoľného bodu ![\small P[x, y] \small P[x, y]](https://lms.umb.sk/filter/tex/pix.php/7e18944b1e340466fd42d0882b61be14.png) určíme dosadením súradníc
určíme dosadením súradníc 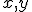 do transformačných rovníc. Napríklad pre
do transformačných rovníc. Napríklad pre ![\small D[3,1] \small D[3,1]](https://lms.umb.sk/filter/tex/pix.php/d87ae2aa6878e674fae0498a5a39d4ee.png) a
a 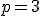 dostaneme
dostaneme ![\small D'[0,-1,0] \small D'[0,-1,0]](https://lms.umb.sk/filter/tex/pix.php/ce1572c3ffb0d63e754073ce9d707f14.png) .
.
Kružnica určená bodmi
![\small A[1, 0], B[0, 1],C[2, 3] \small A[1, 0], B[0, 1],C[2, 3]](https://lms.umb.sk/filter/tex/pix.php/d68e7110804078192907e062e23a2c9c.png) má stred v bode
má stred v bode ![\small S \left [\frac{1}{2}, \frac{1}{2} \right ] \small S \left [\frac{1}{2}, \frac{1}{2} \right ]](https://lms.umb.sk/filter/tex/pix.php/1f862ef6072de16856c6272e4ef49ff7.png) a polomer
a polomer 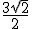 a jej parametrické vyjadrenie má tvar pozrite si prácu "Kružnica, Veta 8"
Tu)
a jej parametrické vyjadrenie má tvar pozrite si prácu "Kružnica, Veta 8"
Tu)![\small \left [\frac{3}{2}, \frac{3}{2} \right ] +\left [\frac{3 \sqrt{2} }{2}\cos t ,\frac{3 \sqrt{2} }{2}\sin t\right ] \small \left [\frac{3}{2}, \frac{3}{2} \right ] +\left [\frac{3 \sqrt{2} }{2}\cos t ,\frac{3 \sqrt{2} }{2}\sin t\right ]](https://lms.umb.sk/filter/tex/pix.php/540ac5353a475dc3c3788ff54a224437.png) .
.
Po dosadení týchto parametrických súradníc do transformačných rovníc, zistíme, že obrazom je elipsa ležiaca v rovine
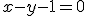 . Jej parametrické vyjadrenie má tvar
. Jej parametrické vyjadrenie má tvar ![\small \left [\frac{3}{2}, \frac{1}{2}, \frac{3}{2} \right ] +\left [-\frac{1}{2}\cos t +\frac{3}{2}\sin t,-\frac{1}{2}\cos t +\frac{3}{2}\sin t, \frac{3}{2}\cos t +\frac{1}{2}\sin t\right ], t, 0, 2π \small \left [\frac{3}{2}, \frac{1}{2}, \frac{3}{2} \right ] +\left [-\frac{1}{2}\cos t +\frac{3}{2}\sin t,-\frac{1}{2}\cos t +\frac{3}{2}\sin t, \frac{3}{2}\cos t +\frac{1}{2}\sin t\right ], t, 0, 2π](https://lms.umb.sk/filter/tex/pix.php/49c8dec70429e172c716a85f61c8fbd7.png) .
.
Príklad zobrazenie 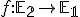 .
.
Určte transformačné rovnice afinného zobrazenia, ktoré zobrazuje body![[2,1], [3,2],[0,1] [2,1], [3,2],[0,1]](https://lms.umb.sk/filter/tex/pix.php/28fd534fed838f9e9fb5d23c36ee99c9.png) do bodov
do bodov ![[2], [0], [10] [2], [0], [10]](https://lms.umb.sk/filter/tex/pix.php/3f02af62885a2f990cca75cf9f4dd6ad.png) v tomto poradí.
v tomto poradí.
Určte obraz ľubovoľného bodu![\small P[x, y] \small P[x, y]](https://lms.umb.sk/filter/tex/pix.php/7e18944b1e340466fd42d0882b61be14.png) a jeho stopu. Príklad je prevzatý z práce (Monoszová, 2.časť, Cvičenie 3.3.2a).
a jeho stopu. Príklad je prevzatý z práce (Monoszová, 2.časť, Cvičenie 3.3.2a).
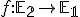 .
.
Určte transformačné rovnice afinného zobrazenia, ktoré zobrazuje body
![[2,1], [3,2],[0,1] [2,1], [3,2],[0,1]](https://lms.umb.sk/filter/tex/pix.php/28fd534fed838f9e9fb5d23c36ee99c9.png) do bodov
do bodov ![[2], [0], [10] [2], [0], [10]](https://lms.umb.sk/filter/tex/pix.php/3f02af62885a2f990cca75cf9f4dd6ad.png) v tomto poradí.
v tomto poradí.
Určte obraz ľubovoľného bodu
![\small P[x, y] \small P[x, y]](https://lms.umb.sk/filter/tex/pix.php/7e18944b1e340466fd42d0882b61be14.png) a jeho stopu. Príklad je prevzatý z práce (Monoszová, 2.časť, Cvičenie 3.3.2a).
a jeho stopu. Príklad je prevzatý z práce (Monoszová, 2.časť, Cvičenie 3.3.2a).
Príklad zobrazenie 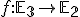 .
.
Určte transformačné rovnice afinného zobrazenia, ktoré zobrazuje body![[1,2,3], [1,1,1],[1,0,1],[0,1,3] [1,2,3], [1,1,1],[1,0,1],[0,1,3]](https://lms.umb.sk/filter/tex/pix.php/d8a837e320e9e2612eac54ce0fc479c3.png) do bodov
do bodov ![[5,4], [2,1], [1,0], [3,2] [5,4], [2,1], [1,0], [3,2]](https://lms.umb.sk/filter/tex/pix.php/5da5cd5c780cbe37d8f10ecca2ada2c3.png) v tomto poradí.
v tomto poradí.
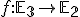 .
.
Určte transformačné rovnice afinného zobrazenia, ktoré zobrazuje body
![[1,2,3], [1,1,1],[1,0,1],[0,1,3] [1,2,3], [1,1,1],[1,0,1],[0,1,3]](https://lms.umb.sk/filter/tex/pix.php/d8a837e320e9e2612eac54ce0fc479c3.png) do bodov
do bodov ![[5,4], [2,1], [1,0], [3,2] [5,4], [2,1], [1,0], [3,2]](https://lms.umb.sk/filter/tex/pix.php/5da5cd5c780cbe37d8f10ecca2ada2c3.png) v tomto poradí.
v tomto poradí.
- Pokúste sa toto afinné zobrazenie geometricky interpretovať pomocou GeoGebry. Príklad je prevzatý z práce (Monoszová, 2.časť, Cvičenie 3.3.7).
- Určte obraz nejakej kružnice a jej stredu.