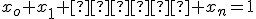Vektorový a afinný priestor
Euklidovský priestor
Lineárna kombinácia bodov
Definícia.
Afinná (barycentrická resp. lineárna) kombinácia bodov. Nech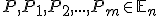 , tak
súčtom (afinnou kombináciou bodov)
, tak
súčtom (afinnou kombináciou bodov) 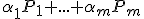 rozumieme bod
rozumieme bod
(AK)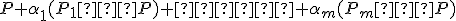 ,
,
pričom pre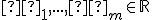 musí platiť
musí platiť 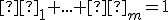 .
.
Afinná (barycentrická resp. lineárna) kombinácia bodov. Nech
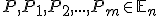 , tak
súčtom (afinnou kombináciou bodov)
, tak
súčtom (afinnou kombináciou bodov) 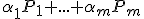 rozumieme bod
rozumieme bod
(AK)
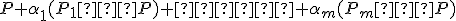 ,
,
pričom pre
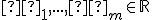 musí platiť
musí platiť 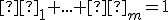 .
.
Dôkaz korektnosti definície.
Treba ukázať, že afinná kombinácia (AK) nezávisí od voľby bodu .
.
Nech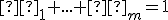 a nech
a nech 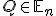 je ľubovoľný bod. Upravujme afinnú kombináciu
je ľubovoľný bod. Upravujme afinnú kombináciu
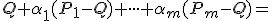
aplikovaním tvrdenia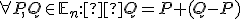 dostaneme
dostaneme
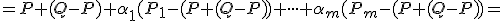
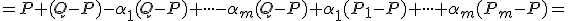
![\small=P + (Q-P)- [(\alpha_1 + \cdot \cdot \cdot + \alpha_m)(Q - P)] + [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] = \small=P + (Q-P)- [(\alpha_1 + \cdot \cdot \cdot + \alpha_m)(Q - P)] + [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] =](https://lms.umb.sk/filter/tex/pix.php/990274bd238b1e5772ccef057aa486e9.png)
![\small = P + [(Q-P)- 1 . (Q − P)]+ [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] = \small = P + [(Q-P)- 1 . (Q − P)]+ [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] =](https://lms.umb.sk/filter/tex/pix.php/8af6504c326498a435d4fe3426f65986.png)
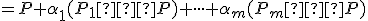 .
.
Čo bolo treba dokázať.
Treba ukázať, že afinná kombinácia (AK) nezávisí od voľby bodu
 .
.
Nech
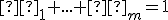 a nech
a nech 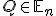 je ľubovoľný bod. Upravujme afinnú kombináciu
je ľubovoľný bod. Upravujme afinnú kombináciu
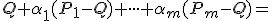
aplikovaním tvrdenia
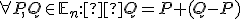 dostaneme
dostaneme
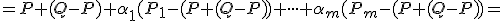
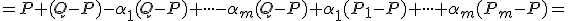
![\small=P + (Q-P)- [(\alpha_1 + \cdot \cdot \cdot + \alpha_m)(Q - P)] + [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] = \small=P + (Q-P)- [(\alpha_1 + \cdot \cdot \cdot + \alpha_m)(Q - P)] + [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] =](https://lms.umb.sk/filter/tex/pix.php/990274bd238b1e5772ccef057aa486e9.png)
![\small = P + [(Q-P)- 1 . (Q − P)]+ [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] = \small = P + [(Q-P)- 1 . (Q − P)]+ [\alpha_1(P_1 - P) + \cdot \cdot \cdot + \alpha_m(P_m - P)] =](https://lms.umb.sk/filter/tex/pix.php/8af6504c326498a435d4fe3426f65986.png)
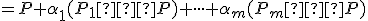 .
.
Čo bolo treba dokázať.
Usporiadaná množina bodov 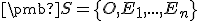 afinného priestoru
afinného priestoru 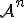 sa nazýva simplex
priestoru
sa nazýva simplex
priestoru 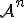 , kde
Teda môžeme zapísať
, kde
Teda môžeme zapísať 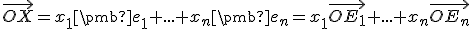 .
.
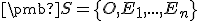 afinného priestoru
afinného priestoru 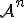 sa nazýva simplex
priestoru
sa nazýva simplex
priestoru 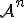 , kde
Teda môžeme zapísať
, kde
Teda môžeme zapísať 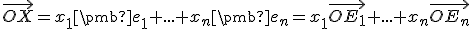 .
.
Dôkaz.
Z vlastnosti (AP1) afinného priestoru vyplýva, že pre ľubovoľný (každý) bod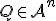 platí
platí
(Q)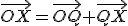 .
.
Vektor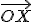 vzhľadom na repér
vzhľadom na repér 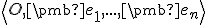 sa dá jednoznačne vyjadriť
ako lineárna kombinácia
sa dá jednoznačne vyjadriť
ako lineárna kombinácia 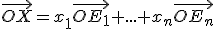 .
.
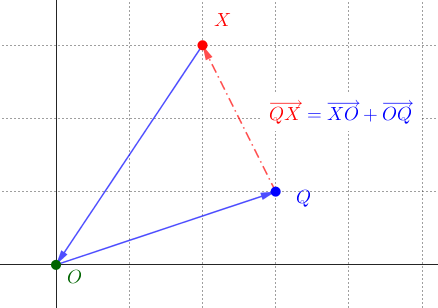 Využitím vzťahov
Využitím vzťahov 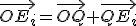 upravme vzťah (Q)
upravme vzťah (Q)
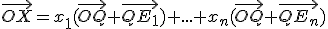 ,
,
odkiaľ
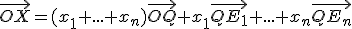 ,
,
Keďže predchádzajúci vzťah nie je závislý od bodu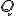 , a keď položíme
, a keď položíme 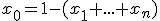 . Potom dostaneme
. Potom dostaneme
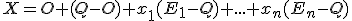
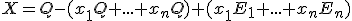
teraz položíme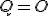 a dostaneme výsledok
a dostaneme výsledok
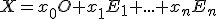
za predpokladu, že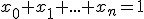 .
.
Z vlastnosti (AP1) afinného priestoru vyplýva, že pre ľubovoľný (každý) bod
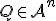 platí
platí
(Q)
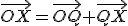 .
.
Vektor
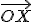 vzhľadom na repér
vzhľadom na repér 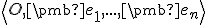 sa dá jednoznačne vyjadriť
ako lineárna kombinácia
sa dá jednoznačne vyjadriť
ako lineárna kombinácia 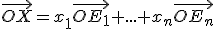 .
.
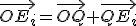 upravme vzťah (Q)
upravme vzťah (Q)
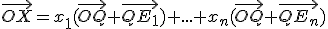 ,
,
odkiaľ
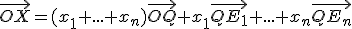 ,
,
Keďže predchádzajúci vzťah nie je závislý od bodu
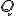 , a keď položíme
, a keď položíme 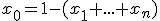 . Potom dostaneme
. Potom dostaneme
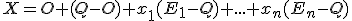
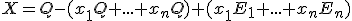
teraz položíme
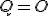 a dostaneme výsledok
a dostaneme výsledok
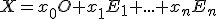
za predpokladu, že
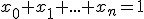 .
.
Pretože rovnosti v dôkaze predošlej vety nezávisia na voľbe bodu 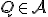 , tak ku každému usporiadanému simplexu
, tak ku každému usporiadanému simplexu  a bodu
a bodu 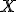 afinného priestoru
afinného priestoru 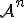 existuje jediná sústava skalárov
existuje jediná sústava skalárov 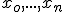 tak,
že platí rovnosť uvedená v tejto vete. Zrejme platí aj obrátená veta: Každá sústava skalárov
tak,
že platí rovnosť uvedená v tejto vete. Zrejme platí aj obrátená veta: Každá sústava skalárov 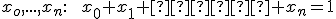 jednoznačne určuje bod
jednoznačne určuje bod 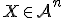 , pre ktorý platí tvrdenie vety.
, pre ktorý platí tvrdenie vety.
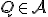 , tak ku každému usporiadanému simplexu
, tak ku každému usporiadanému simplexu  a bodu
a bodu 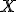 afinného priestoru
afinného priestoru 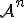 existuje jediná sústava skalárov
existuje jediná sústava skalárov 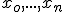 tak,
že platí rovnosť uvedená v tejto vete. Zrejme platí aj obrátená veta: Každá sústava skalárov
tak,
že platí rovnosť uvedená v tejto vete. Zrejme platí aj obrátená veta: Každá sústava skalárov 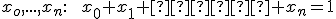 jednoznačne určuje bod
jednoznačne určuje bod 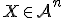 , pre ktorý platí tvrdenie vety.
, pre ktorý platí tvrdenie vety.
Z dôkazu predchádzajúcej vety vyplýva, že súčet 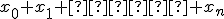 je rovný jednej. Preto podmienka
je rovný jednej. Preto podmienka 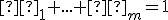 v definícii afinnej kombinácii bodov je dôležitá a nutná.
v definícii afinnej kombinácii bodov je dôležitá a nutná.
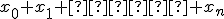 je rovný jednej. Preto podmienka
je rovný jednej. Preto podmienka 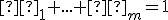 v definícii afinnej kombinácii bodov je dôležitá a nutná.
v definícii afinnej kombinácii bodov je dôležitá a nutná.
Cvičenie.
- Nech
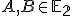 sú dva rôzne body. Zistite, aký bod predstavuje lineárna kombinácia
sú dva rôzne body. Zistite, aký bod predstavuje lineárna kombinácia 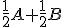 .
. - Nech
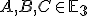 sú tri nekolineárne body. Zistite, ktorý bod predstavuje lineárna kombinácia
sú tri nekolineárne body. Zistite, ktorý bod predstavuje lineárna kombinácia
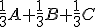 . Vyjadrite pomocou lineárnej kombinácie vrcholov trojuholníka
. Vyjadrite pomocou lineárnej kombinácie vrcholov trojuholníka  ľubovoľný vnútorný bod tohto trojuholníka.
ľubovoľný vnútorný bod tohto trojuholníka. - ♥ Vyjadrite pomocou lineárnej kombinácie nezávislých bodov
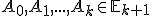 ľubovoľný bod podpriestoru
ľubovoľný bod podpriestoru 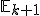 určeného týmito bodmi.
určeného týmito bodmi.
Riešenie.
- Upravujme
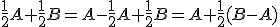 ,
,
čo predstavuje stred úsečky . Zobrazte túto situáciu v GeoGebre.
. Zobrazte túto situáciu v GeoGebre. - Znázornite túto situáciu v GeoGebre, otvorte si zadanie Tu. Riešenie Tu.
- Podľa vety "bod ako kombinácia simplexu" pre bod
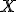 podpriestoru
podpriestoru 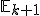 a jeho simplex
a jeho simplex 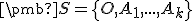 platí
platí
(Mx)![\small X=[1-(x_1+· · · + x_k)]O + x_1A_1 + · · · + x_kA_k \small X=[1-(x_1+· · · + x_k)]O + x_1A_1 + · · · + x_kA_k](https://lms.umb.sk/filter/tex/pix.php/248ac2c5f0e61b17c1a1ab3d3edb6013.png) .
.
Po jednoduchej úprave dostaneme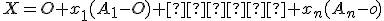 ,
,
čo predstavuje bod podpriestoru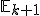 .
.
- Pre podpriestor
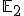 množina všetkých bodov
množina všetkých bodov 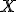 spĺňajúcich podmienku (Mx) je zrejme priamka (útvar určený dvoma nezávislými bodmi).
Jej parametrické vyjadrenie má tvar
spĺňajúcich podmienku (Mx) je zrejme priamka (útvar určený dvoma nezávislými bodmi).
Jej parametrické vyjadrenie má tvar
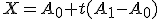 .
.
Po úprave dostaneme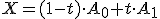 ,
,
čo predstavuje lineárnu kombináciu bodov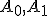 .
. - Pre podpriestor
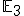 to bude rovina (útvar určený tromi nezávislými bodmi). Jej parametrické vyjadrenie má
tvar
to bude rovina (útvar určený tromi nezávislými bodmi). Jej parametrické vyjadrenie má
tvar 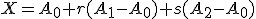 .
.
Po úprave dostaneme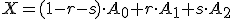 ,
,
čo predstavuje lineárnu kombináciu bodov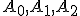 .
.
- Pre podpriestor
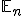
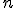
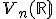
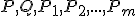
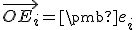
![\small [x_1, . . . , x_n] \small [x_1, . . . , x_n]](https://lms.umb.sk/filter/tex/pix.php/4a8ded17926937e08716405dcff18ab2.png)