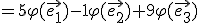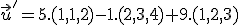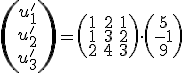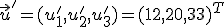Vektorový a afinný priestor
Vektorový priestor
Súradnice v báze
Príklad.
Riešenie.
- Zrejme
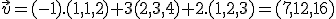 .
.
Toto sú súradnice vektora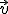 vzhľadom k jednotkovej báze. Je dôležité dodržať poradie prvkov bázy
vzhľadom k jednotkovej báze. Je dôležité dodržať poradie prvkov bázy  .
. - Určiť súradnice vzhľadom k báze
 znamená vektor
znamená vektor 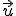 vyjadriť ako lineárnu kombináciu prvkov bázy
vyjadriť ako lineárnu kombináciu prvkov bázy  .
Opäť treba dať pozor na poradie prvkov bázy. Musíme nájsť
.
Opäť treba dať pozor na poradie prvkov bázy. Musíme nájsť 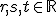 , pre ktoré platí:
, pre ktoré platí:
( i)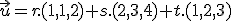 resp.
resp.
( ii):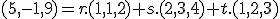 .
.
Úlohu môžeme riešiť ako sústavu rovníc (vyriešte úlohu týmto spôsobom).
(iii):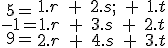
alebo rovnosť (ii) prepíšeme na maticový tvar (vektory bázy zapisujeme do stĺpcov! Prečo?) takto:
(iv):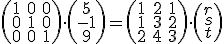
Vyjadriť vektor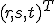 (transponovaný zápis vektora) môžeme tak, že obe strany rovnice (iv) vynásobíme zľava inverznou maticou
(transponovaný zápis vektora) môžeme tak, že obe strany rovnice (iv) vynásobíme zľava inverznou maticou
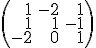 .
.
Inverznú maticu určíme napríklad pomocou programu GeoGebra, otvorte si applet "inverzná matica" Tu. Po vynásobení zľava obidvoch strán rovnice (iv) dostaneme
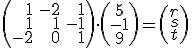 .
.
Riešením je vektor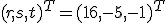 . Otvorte si výpočty v GeoGebre
Tu.
. Otvorte si výpočty v GeoGebre
Tu.
Nasledujúci applet demonštruje určenie súradníc vektora 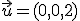 v báze
v báze 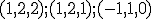 Riešením sú súradnice
Riešením sú súradnice 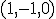 . Vypočítajte ich pomocou maticového tvaru, pričom využite program Matrix calculator.
. Vypočítajte ich pomocou maticového tvaru, pričom využite program Matrix calculator.
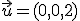 v báze
v báze 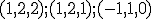 Riešením sú súradnice
Riešením sú súradnice 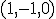 . Vypočítajte ich pomocou maticového tvaru, pričom využite program Matrix calculator.
. Vypočítajte ich pomocou maticového tvaru, pričom využite program Matrix calculator.
♥ Príklad.
Je dané lineárne zobrazenie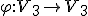 , ktoré jednotkovú bázu
, ktoré jednotkovú bázu 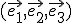 zobrazí na bázu
zobrazí na bázu 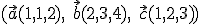 priestoru
priestoru 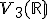 . Nájdite obraz
. Nájdite obraz 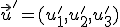 vektora
vektora 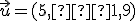 v tomto zobrazení.
v tomto zobrazení.
Je dané lineárne zobrazenie
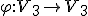 , ktoré jednotkovú bázu
, ktoré jednotkovú bázu 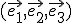 zobrazí na bázu
zobrazí na bázu 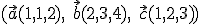 priestoru
priestoru 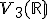 . Nájdite obraz
. Nájdite obraz 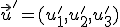 vektora
vektora 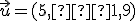 v tomto zobrazení.
v tomto zobrazení.
Poznámka
Nech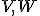 sú vektorové priestory nad telesom
sú vektorové priestory nad telesom 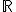 . Zobrazenie
. Zobrazenie 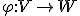 sa nazýva lineárne zobrazenie, ak je splnené nasledovné:
sa nazýva lineárne zobrazenie, ak je splnené nasledovné:
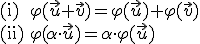
kde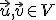 a
a 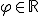 .
.
Nech
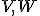 sú vektorové priestory nad telesom
sú vektorové priestory nad telesom 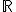 . Zobrazenie
. Zobrazenie 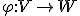 sa nazýva lineárne zobrazenie, ak je splnené nasledovné:
sa nazýva lineárne zobrazenie, ak je splnené nasledovné:
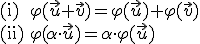
kde
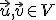 a
a 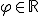 .
.
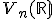

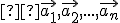
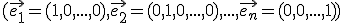
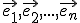
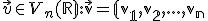
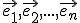
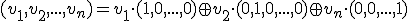
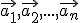
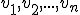
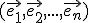
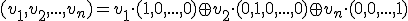
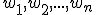
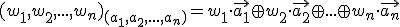
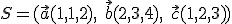
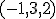
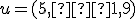
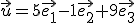
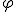
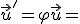
![\small =\varphi[ 5\vec{e_1})-1(\vec{e_2})+9(\vec{e_3}) ] \small =\varphi[ 5\vec{e_1})-1(\vec{e_2})+9(\vec{e_3}) ]](https://lms.umb.sk/filter/tex/pix.php/cd03d29993f1d054825e7f80121467a8.png)
![\small = \varphi[5.(1,0,0) + (-1)(0,1,0) + 9.(0,0, 1)] \small = \varphi[5.(1,0,0) + (-1)(0,1,0) + 9.(0,0, 1)]](https://lms.umb.sk/filter/tex/pix.php/915591b915a760ee30ed194304ba7e21.png)