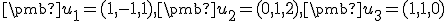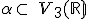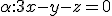Vektorový a afinný priestor
Vektorový priestor
Schmidt ortogon. proces
Nech 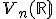 je
je 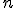 - rozmerný vektorový priestor so skalárnym súčinom
- rozmerný vektorový priestor so skalárnym súčinom 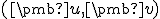 a nech je daná množina
a nech je daná množina 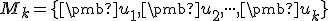 lineárne nezávislých vektorov tohto konečno rozmerného priestoru (
lineárne nezávislých vektorov tohto konečno rozmerného priestoru (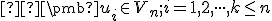 ).
).
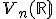 je
je 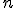 - rozmerný vektorový priestor so skalárnym súčinom
- rozmerný vektorový priestor so skalárnym súčinom 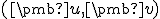 a nech je daná množina
a nech je daná množina 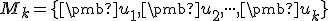 lineárne nezávislých vektorov tohto konečno rozmerného priestoru (
lineárne nezávislých vektorov tohto konečno rozmerného priestoru (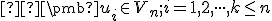 ).
).
Definícia.
Schmidtov ortogonalizačný proces je proces, ktorým z množiny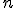 lineárne nezávislých vektorov vytvárame ortonormálnu bázu
lineárne nezávislých vektorov vytvárame ortonormálnu bázu 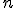 - rozmerného
vektorového priestoru
- rozmerného
vektorového priestoru 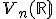 .
.
Schmidtov ortogonalizačný proces je proces, ktorým z množiny
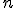 lineárne nezávislých vektorov vytvárame ortonormálnu bázu
lineárne nezávislých vektorov vytvárame ortonormálnu bázu 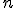 - rozmerného
vektorového priestoru
- rozmerného
vektorového priestoru 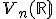 .
.
Poznámka.
Ortonormálna báza sa vyznačuje vlastnosťou, že jej vektory majú normovanú jednotkovú dĺžku a všetky sú navzájom kolmé (ortogonálne).
Existenciu takejto ortonormálnej bázy zabezpečuje Veta - Schmidtov ortogonalizačný proces.
Ortonormálna báza sa vyznačuje vlastnosťou, že jej vektory majú normovanú jednotkovú dĺžku a všetky sú navzájom kolmé (ortogonálne).
Existenciu takejto ortonormálnej bázy zabezpečuje Veta - Schmidtov ortogonalizačný proces.
Celý proces vytvárania ortonormálnej bázy možno popísať algoritmicky/rekurentne takto:
- V prvom kroku Schmidtovho ortogonalizačného procesu sa za základ stanoví prvý vektor z danej množiny vektorov
 . Podľa tohto vektora sa odvíja orientácia
zvyšných.
. Podľa tohto vektora sa odvíja orientácia
zvyšných. - Ďalším
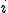 -tym krokom je samotná ortogonalizácia
-tym krokom je samotná ortogonalizácia 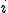 -teho vektora. Nasledujúci
-teho vektora. Nasledujúci 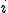 -ty vektor určíme ako lineárnu
kombináciu
-ty vektor určíme ako lineárnu
kombináciu 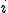 -teho vektora z danej množiny vektorov
-teho vektora z danej množiny vektorov  a už
a už 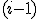 vytvorených vektorov.
vytvorených vektorov. - Nakoniec prevedieme normalizáciu vektorov. Pre zjednodušenie výpočtov sa vektory normalizujú až na koniec procesu.
Veta - Schmidtov ortogonalizačný proces.
Nech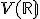 je vektorový priestor so skalárnym súčinom
je vektorový priestor so skalárnym súčinom
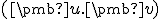 a nech
a nech 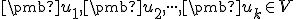 sú lineárne nezávislé vektory. Potom existujú
ortonormálne vektory
sú lineárne nezávislé vektory. Potom existujú
ortonormálne vektory 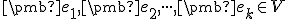 , pre ktoré platí
, pre ktoré platí
![\small [{\pmb {e_1}, \pmb {e_2}, \cdot \cdot \cdot, \pmb {e_i}}] = [{\pmb {u_1}, \pmb {u_2}, \cdot \cdot \cdot, \pmb {u_i}}], ∀i ∈ {1, 2, . . . , k} \small [{\pmb {e_1}, \pmb {e_2}, \cdot \cdot \cdot, \pmb {e_i}}] = [{\pmb {u_1}, \pmb {u_2}, \cdot \cdot \cdot, \pmb {u_i}}], ∀i ∈ {1, 2, . . . , k}](https://lms.umb.sk/filter/tex/pix.php/e1015ffff519181270c72c15a0dc8bcc.png)
Nech
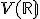 je vektorový priestor so skalárnym súčinom
je vektorový priestor so skalárnym súčinom
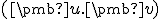 a nech
a nech 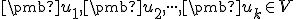 sú lineárne nezávislé vektory. Potom existujú
ortonormálne vektory
sú lineárne nezávislé vektory. Potom existujú
ortonormálne vektory 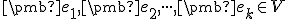 , pre ktoré platí
, pre ktoré platí
![\small [{\pmb {e_1}, \pmb {e_2}, \cdot \cdot \cdot, \pmb {e_i}}] = [{\pmb {u_1}, \pmb {u_2}, \cdot \cdot \cdot, \pmb {u_i}}], ∀i ∈ {1, 2, . . . , k} \small [{\pmb {e_1}, \pmb {e_2}, \cdot \cdot \cdot, \pmb {e_i}}] = [{\pmb {u_1}, \pmb {u_2}, \cdot \cdot \cdot, \pmb {u_i}}], ∀i ∈ {1, 2, . . . , k}](https://lms.umb.sk/filter/tex/pix.php/e1015ffff519181270c72c15a0dc8bcc.png)
Dôkaz.
A. Proces ortogonalizácie.
A. Proces ortogonalizácie.
- Najprv určíme prvý vektor, pričom položíme
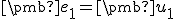 .
. - Druhý vektor určíme ako lineárnu kombináciu
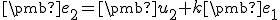 , pričom podľa predpokladu platí
, pričom podľa predpokladu platí 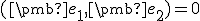 .
Po skalárnom vynásobení
rovnice
.
Po skalárnom vynásobení
rovnice 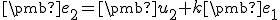 vektorom
vektorom 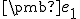 dostaneme riešenie
dostaneme riešenie
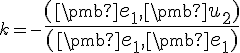 .
.
Po dosadení dostaneme riešenie
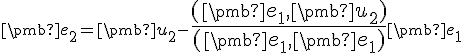 .
. - Pre tretí vektor bude lineárna kombinácia v tvare
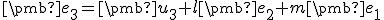 , pričom platí
, pričom platí 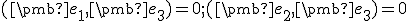 .
Po skalárnom vynásobení rovnice postupne vektormi
.
Po skalárnom vynásobení rovnice postupne vektormi 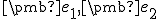 dostaneme riešenie
dostaneme riešenie
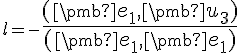 ;
; 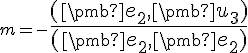 .
. - Pomocou matematickej indukcie dokážeme, že pre ďalšie vektory platia vzťahy
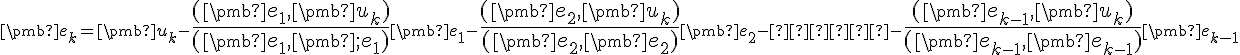 .
. - Teraz stačí len "znormovať" tieto vektory.
Dostaneme jednotkové vektory
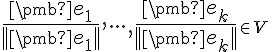
Cvičenie.
Riešenie.
- Zvoľme prvý vektor ortogonálnej bázy
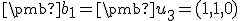 (zrejme nie je jednotkový, jeho normalizáciu urobíme v závere riešenia). Druhý
vektor
(zrejme nie je jednotkový, jeho normalizáciu urobíme v závere riešenia). Druhý
vektor 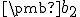 určíme zo vzťahu
určíme zo vzťahu
(k)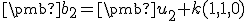 ,
,
kde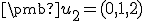 . Rovnicu (k) skalárne vynásobíme vektorom
. Rovnicu (k) skalárne vynásobíme vektorom 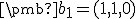 . Podľa predpokladu v Schmidtovom ortogonalizačnom procese musia
byť vektory
. Podľa predpokladu v Schmidtovom ortogonalizačnom procese musia
byť vektory 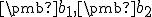 na seba kolmé, teda musí pre ich skalárny súčin platiť rovnosť
na seba kolmé, teda musí pre ich skalárny súčin platiť rovnosť 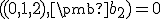 . Zároveň platí
. Zároveň platí
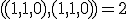 . Po dosadení do (k) môžeme určiť/vypočítať koeficient
. Po dosadení do (k) môžeme určiť/vypočítať koeficient
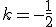 , odkiaľ dostaneme pre vektor
, odkiaľ dostaneme pre vektor 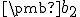
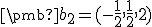 .
.
Tretí vektor určíme zo vzťahu
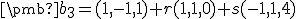
(zobrali sme 2-násobok druhého vektora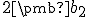 ). Ľahko nahliadneme, že
). Ľahko nahliadneme, že 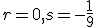 , odkiaľ
, odkiaľ 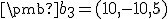 . Zrejme
vektory
. Zrejme
vektory 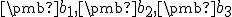 sú na seba kolmé a stačí ich znormovať.
sú na seba kolmé a stačí ich znormovať.
V prípade, že by sme zvolili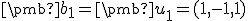 dostali by sme bázu
dostali by sme bázu 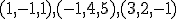 , ktorá je tiež ortogonálna.
Teda výsledná báza závisí od voľby poradia vektorov
, ktorá je tiež ortogonálna.
Teda výsledná báza závisí od voľby poradia vektorov 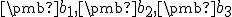 .
.
- Stačí určiť smerové vektory danej roviny, ktoré patria do vektorového priestoru určeného danou rovinou (do jej zamerania). Sú to napríklad vektory
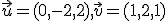 .
Potom realizujte Schmidtov ortogonalizačný proces a utvorte ortogonálnu bázu skúmaného vektorového podpriestoru.
.
Potom realizujte Schmidtov ortogonalizačný proces a utvorte ortogonálnu bázu skúmaného vektorového podpriestoru.
Preštudujte si študijný text o kolmých vektorových podpriestoroch v práci:
Monoszová, G.: Analytická geometria 2 - Kapitola III. FPV UMB B. Bystrica. Časť II. 2. Totalne kolmé vektorové priestory. Kolmé vektorové priestory.
Monoszová, G.: Analytická geometria 2 - Kapitola III. FPV UMB B. Bystrica. Časť II. 2. Totalne kolmé vektorové priestory. Kolmé vektorové priestory.