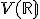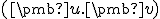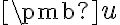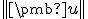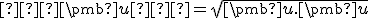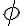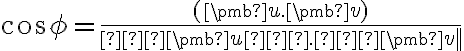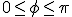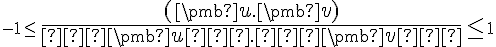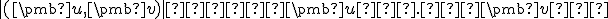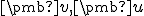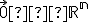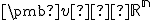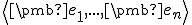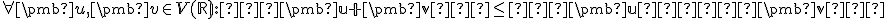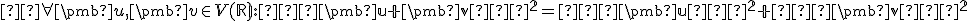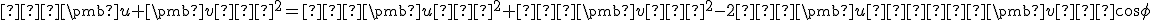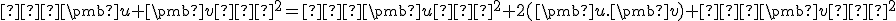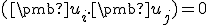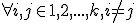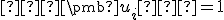Vektorový a afinný priestor
Vektorový priestor
Cauchy-Schwarz nerov.
Tvrdenia.
Dôkaz - Cauchy-Schwarzovej nerovnosti.
- Pre lineárne závislé vektory
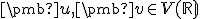 musí existovať nenulové reálne číslo
musí existovať nenulové reálne číslo  , pre ktoré platí
, pre ktoré platí 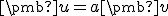 .
Ak sú vektory nezávislé tak, pre každé nenulové reálne číslo
.
Ak sú vektory nezávislé tak, pre každé nenulové reálne číslo  vektor
vektor 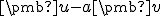 je nenulový. Zrejme druhá mocnina jeho normy je
je nenulový. Zrejme druhá mocnina jeho normy je 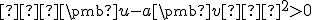 a nie je rovná nule. Podľa definície normy rozpíšeme ľavú stranu nerovnosti ako
a nie je rovná nule. Podľa definície normy rozpíšeme ľavú stranu nerovnosti ako
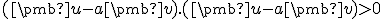
Skalárny súčin je symetrický a distributívny, preto po úprave dostaneme kvadratickú nerovnicu .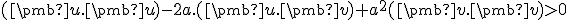
Ľavá strana nerovnice predstavuje kvadratický trojčlen v premennej , ktorý nemá reálne korene (pre ľubovoľnú hodnotu
, ktorý nemá reálne korene (pre ľubovoľnú hodnotu  je trojčlen > 0).
Jej diskriminant musí byť záporný, teda platí
je trojčlen > 0).
Jej diskriminant musí byť záporný, teda platí
![\small D= [−2(\pmb u.\pmb v)]^2−4∥\pmb u∥^2∥\pmb v∥|^2 < 0 \small D= [−2(\pmb u.\pmb v)]^2−4∥\pmb u∥^2∥\pmb v∥|^2 < 0](https://lms.umb.sk/filter/tex/pix.php/5d1d6a6c21a1552053a44c66b0d48907.png)
Odtiaľ už ľahko dostaneme![\small [−2(\pmb u.\pmb v)]^2 < 4∥\pmb u∥^2∥\pmb v∥^2 \small [−2(\pmb u.\pmb v)]^2 < 4∥\pmb u∥^2∥\pmb v∥^2](https://lms.umb.sk/filter/tex/pix.php/142c3980a2c61a0d1fb666f35dec9692.png) a po odmocnení
a po odmocnení 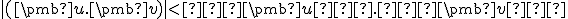 .
.
- Dôkaz pre lineárne závislé vektory prenechávame čitateľovi. Zrejme bude platiť rovnosť strán.
Dôkazy.
- Na úrovni VŠ použite Cauchy-Schwarzovu nerovnosť. Podrobné dôkazy nájdete v
"Sbírce řešených úloh Katedřy didaktiky fyziky Matematicko-fyzikální fakulty UK Praha". Tu.
Vezmite normu (druhú mocninu normy) na ľavej strane nerovnosti a prepíšte ju podľa definície pomocou skalárneho súčinu. Výraz zjednodušte vďaka linearite a symetrii skalárneho súčinu. - Na úrovni SŠ použite Cauchy-Schwarzovu nerovnosť ale pre prípad vektorového priestoru
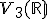 so štandardnou ortonormálnou
bázou
so štandardnou ortonormálnou
bázou 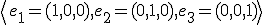 . Pre vektory
. Pre vektory 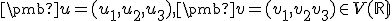 je skalárny súčin definovaný ako
je skalárny súčin definovaný ako
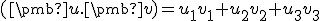 .
.
Cvičenie.
- Skalárny súčin je definovaný na
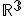 takto:
takto:
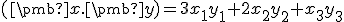 .
.
pre![\small \pmb x = [x_1, x_2, x_3], \pmb y = [y_1, y_2, y_3] \in \mathbb R^3 \small \pmb x = [x_1, x_2, x_3], \pmb y = [y_1, y_2, y_3] \in \mathbb R^3](https://lms.umb.sk/filter/tex/pix.php/6c5a6b65e8aa73603a0a02071a6ebf6e.png) . Určte číslo
. Určte číslo 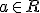 tak,
aby vektory
tak,
aby vektory ![\small \pmb x = [a-1, 3, a+1], \pmb y = [-4, -a, 3a] \small \pmb x = [a-1, 3, a+1], \pmb y = [-4, -a, 3a]](https://lms.umb.sk/filter/tex/pix.php/751ef74e6076cb8898fad9ed0f878e3e.png) boli na seba kolmé v zmysle definície kolmosti vektorov. Aký reálny uhol zvierajú tieto vektory v euklidovskom 3-rozmernom priestore? (Ukážte, že táto operácia spĺňa podmienky skalárneho súčinu).
boli na seba kolmé v zmysle definície kolmosti vektorov. Aký reálny uhol zvierajú tieto vektory v euklidovskom 3-rozmernom priestore? (Ukážte, že táto operácia spĺňa podmienky skalárneho súčinu). - Body
![\small A[-3,2],B[2,4] \small A[-3,2],B[2,4]](https://lms.umb.sk/filter/tex/pix.php/6c440150c22d1ac8d7c3e62d5d7e5753.png) sú susedné vrcholy štvorca. Pomocou skalárneho súčinu určte súradnice jeho zvyšných vrcholov.
sú susedné vrcholy štvorca. Pomocou skalárneho súčinu určte súradnice jeho zvyšných vrcholov.
Riešenie.
- Pomocou bilineárnych foriem ukážte, že operácia spĺňa podmienky skalárneho súčinu (použitie bilineárnych foriem na zdôvodnenie tvrdenia nájdete Tu).
Ak vektory
![\small \pmb x = [a-1, 3, a+1], \pmb y = [-4, -a, 3a] \small \pmb x = [a-1, 3, a+1], \pmb y = [-4, -a, 3a]](https://lms.umb.sk/filter/tex/pix.php/751ef74e6076cb8898fad9ed0f878e3e.png) majú byť na seba kolmé, tak ich skalárny súčin sa musí rovnať nule. Po dosadení dostaneme
majú byť na seba kolmé, tak ich skalárny súčin sa musí rovnať nule. Po dosadení dostaneme
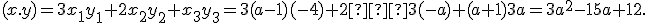
Riešením kvadratickej rovnice sú čísla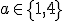 . Pozrite si grafické riešenie
Tu.
. Pozrite si grafické riešenie
Tu. -
Pre skalárny súčin platí
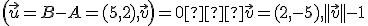 .
.