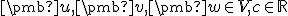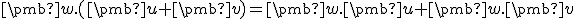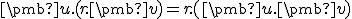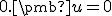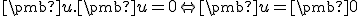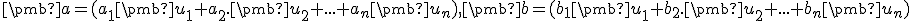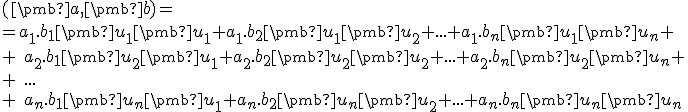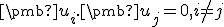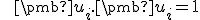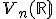Vektorový a afinný priestor
Vektorový priestor
Skalárny súčin
Definícia, vlastnosti (zopakovanie z Lineárnej algebry).
Definícia.
Nech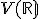 je vektorový priestor nad poľom reálnych čísel. Zobrazenie (operáciu)
je vektorový priestor nad poľom reálnych čísel. Zobrazenie (operáciu)
 :
: 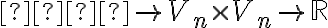
nazveme skalárny súčin na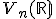 , ak pre každé
, ak pre každé 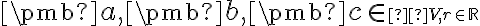 sú splnené tieto podmienky:
sú splnené tieto podmienky:
Nech
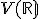 je vektorový priestor nad poľom reálnych čísel. Zobrazenie (operáciu)
je vektorový priestor nad poľom reálnych čísel. Zobrazenie (operáciu)
 :
: 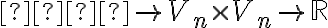
nazveme skalárny súčin na
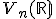 , ak pre každé
, ak pre každé 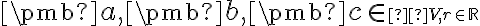 sú splnené tieto podmienky:
sú splnené tieto podmienky:
Poznámky.
- Vlastnosti (ii) a (iii) nastavujú požiadavku na linearitu v prvej zložke. Vlastnosť (i) žiada symetriu, tj linearita prvej zložky sa prenáša do zložky druhej. Tieto vlastnosti má symetrická bilineárna forma. Viac o bilineárnych formách nájdete Tu.
- Vlastnosť (iv) hovorí, že forma musí byť pozitívne definitívna.
- Skalárny súčin na reálnom priestore je teda symetrická pozitívne definitná bilineárna forma na danom priestore.
- Takto definovaný skalárny súčin sa často v literatúre označuje ako vážený skalárny súčin.
- Pre skalárny súčin na reálnom priestore budeme namiesto označenia
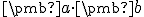 používať len symbol pre násobenie
používať len symbol pre násobenie 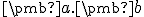 alebo symbol usporiadanej dvojice
alebo symbol usporiadanej dvojice 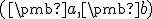 .
.
Vážený skalárny súčin je oproti „stredoškolskému skalárnemu súčinu“ oveľa všeobecnejší. Stredoškolsky definovaný skalárny súčin (tiež nazývaný aj ako euklidovský skalárny súčin) na priestore 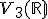 je zavedený nasledovne. Ak
je zavedený nasledovne. Ak ![\small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3] \small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3]](https://lms.umb.sk/filter/tex/pix.php/cad0163933a5d2adf5e1bcaed21e570d.png) , tak
, tak
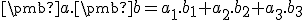
Presvedčte sa, že stredoškolsky definovaný skalárny súčin spĺňa podmienky uvedené v definícii, že je to symetrická pozitívne definitná bilineárna forma.
Definícia skalárneho súčinu môže mať rôzne podoby. Napríklad na množine spojitých funkcií intervalu ⟨a,b⟩ možno uvažovať skalárny súčin vo forme
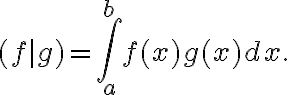
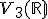 je zavedený nasledovne. Ak
je zavedený nasledovne. Ak ![\small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3] \small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3]](https://lms.umb.sk/filter/tex/pix.php/cad0163933a5d2adf5e1bcaed21e570d.png) , tak
, tak
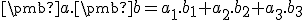
Presvedčte sa, že stredoškolsky definovaný skalárny súčin spĺňa podmienky uvedené v definícii, že je to symetrická pozitívne definitná bilineárna forma.
Definícia skalárneho súčinu môže mať rôzne podoby. Napríklad na množine spojitých funkcií intervalu ⟨a,b⟩ možno uvažovať skalárny súčin vo forme
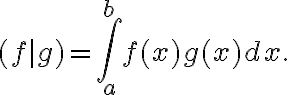
Riešenie.
Dosadením súradníc vektorov![\small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3], \pmb c = [c_1, c_2, c_3] \in \mathbb R^3 \small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3], \pmb c = [c_1, c_2, c_3] \in \mathbb R^3](https://lms.umb.sk/filter/tex/pix.php/0f2b26f65693e348a81b8428fbc61ab7.png) do definície skalárneho súčinu,
ľahko overíme, že jednotlivé podmienky v definícii sú splnené.
do definície skalárneho súčinu,
ľahko overíme, že jednotlivé podmienky v definícii sú splnené.
Riešenie pomocou bilineárnych foriem nájdete Tu.
Dosadením súradníc vektorov
![\small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3], \pmb c = [c_1, c_2, c_3] \in \mathbb R^3 \small \pmb a = [a_1, a_2, a_3], \pmb b = [b_1, b_2, b_3], \pmb c = [c_1, c_2, c_3] \in \mathbb R^3](https://lms.umb.sk/filter/tex/pix.php/0f2b26f65693e348a81b8428fbc61ab7.png) do definície skalárneho súčinu,
ľahko overíme, že jednotlivé podmienky v definícii sú splnené.
do definície skalárneho súčinu,
ľahko overíme, že jednotlivé podmienky v definícii sú splnené.
Riešenie pomocou bilineárnych foriem nájdete Tu.
Veta - ďalšie vlastnosti skalárneho súcinu.
Veta - určenie euklidovského skalárneho súčinu.
Nech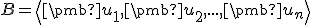 je ortonormálna báza vektorového priestoru
je ortonormálna báza vektorového priestoru 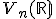 a
nech
a
nech 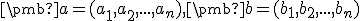 sú súradnice vektorov
sú súradnice vektorov 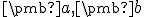 v báze
v báze 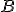 . Potom
. Potom
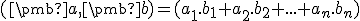 .
.
Nech
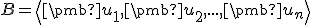 je ortonormálna báza vektorového priestoru
je ortonormálna báza vektorového priestoru 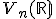 a
nech
a
nech 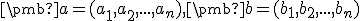 sú súradnice vektorov
sú súradnice vektorov 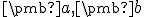 v báze
v báze 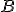 . Potom
. Potom
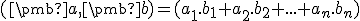 .
.
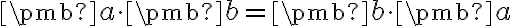
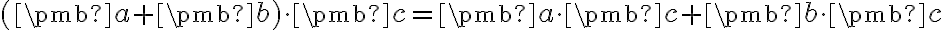
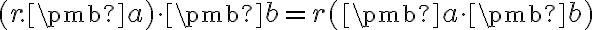
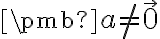
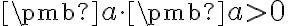

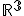
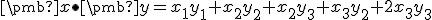
![\small \pmb x = [x_1, x_2, x_3], \pmb y = [y_1, y_2, y_3] \in \mathbb R^3 \small \pmb x = [x_1, x_2, x_3], \pmb y = [y_1, y_2, y_3] \in \mathbb R^3](https://lms.umb.sk/filter/tex/pix.php/6c5a6b65e8aa73603a0a02071a6ebf6e.png)