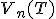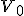Vektorový a afinný priestor
Vektorový priestor
Dimenzia a báza
Nech 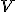 je vektorový priestor nad telesom
je vektorový priestor nad telesom 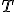 . Po zavedení pojmov lineárna závislosť a lineárna nezávislosť sme zadefinovali lineárny obal ako
množinu všetkých lineárnych kombinácií
kde
. Po zavedení pojmov lineárna závislosť a lineárna nezávislosť sme zadefinovali lineárny obal ako
množinu všetkých lineárnych kombinácií
kde 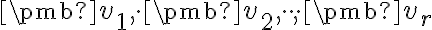 sú vopred dané vektory priestoru
sú vopred dané vektory priestoru 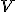 .
.
Teraz môžeme pristúpiť k pojmom dimenzia a báza vektorového priestoru. Predtým musíme a pridať niektoré vektorové axiómy.
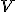 je vektorový priestor nad telesom
je vektorový priestor nad telesom 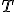 . Po zavedení pojmov lineárna závislosť a lineárna nezávislosť sme zadefinovali lineárny obal ako
množinu všetkých lineárnych kombinácií
kde
. Po zavedení pojmov lineárna závislosť a lineárna nezávislosť sme zadefinovali lineárny obal ako
množinu všetkých lineárnych kombinácií
kde 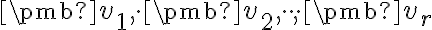 sú vopred dané vektory priestoru
sú vopred dané vektory priestoru 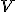 .
.
Teraz môžeme pristúpiť k pojmom dimenzia a báza vektorového priestoru. Predtým musíme a pridať niektoré vektorové axiómy.
Axiómy dimenzie - rozmeru
- Nech vo vektorovom priestore
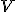 existuje maximálne
existuje maximálne 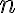 lineárne nezávislých vektorov, kde
lineárne nezávislých vektorov, kde 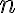 je prirodzené číslo.
Číslo
je prirodzené číslo.
Číslo  nazývame dimenzia vektorového priestoru.
nazývame dimenzia vektorového priestoru. - Každá
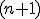 - tica vektorov je už lineárne závislá.
- tica vektorov je už lineárne závislá. - Podmnožina
 vektorového priestoru
vektorového priestoru 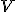 je jeho báza práve vtedy, keď každý vektor
je jeho báza práve vtedy, keď každý vektor 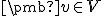 možno práve jediným spôsobom
vyjadriť ako lineárnu kombináciu
možno práve jediným spôsobom
vyjadriť ako lineárnu kombináciu 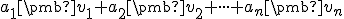 navzájom rôznych vektorov množiny
navzájom rôznych vektorov množiny  .
. - Koeficienty
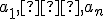 nazývame súradnice vektora v vzhľadom na bázu
nazývame súradnice vektora v vzhľadom na bázu  . Označujeme
. Označujeme 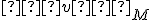 a čítame „súradnice vektora
a čítame „súradnice vektora 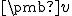 vzhľadom na bázu
vzhľadom na bázu  .
.
Definícia.
Vektorový priestor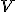 nad telesom
nad telesom 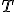 je konečno-rozmerný, ak existuje taká konečná
množina vektorov
je konečno-rozmerný, ak existuje taká konečná
množina vektorov 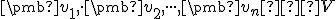 , že platí
, že platí
![\small V =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_n}\pmb] \small V =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_n}\pmb]](https://lms.umb.sk/filter/tex/pix.php/d96af90db420b599197cd8a21f7ba21b.png) .
.
Báza je množina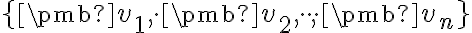 lineárne nezávislých vektorov,
ktorá generuje celý priestor
lineárne nezávislých vektorov,
ktorá generuje celý priestor 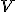 .
.
Vektorový priestor
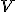 nad telesom
nad telesom 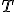 je konečno-rozmerný, ak existuje taká konečná
množina vektorov
je konečno-rozmerný, ak existuje taká konečná
množina vektorov 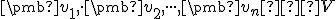 , že platí
, že platí
![\small V =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_n}\pmb] \small V =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_n}\pmb]](https://lms.umb.sk/filter/tex/pix.php/d96af90db420b599197cd8a21f7ba21b.png) .
.
Báza je množina
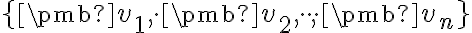 lineárne nezávislých vektorov,
ktorá generuje celý priestor
lineárne nezávislých vektorov,
ktorá generuje celý priestor 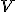 .
.
Príklad.
Majme množinu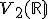 všetkých usporiadaných dvojíc reálnych čísel a operácie:
všetkých usporiadaných dvojíc reálnych čísel a operácie:
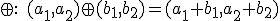 - sčítanie po zložkách.
- sčítanie po zložkách.
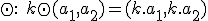 - násobenie skalárom
- násobenie skalárom 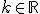 ,
,
kde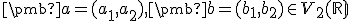 sú ľubovoľné usporiadané dvojice reálnych čísel. Ukážte, že
množina
sú ľubovoľné usporiadané dvojice reálnych čísel. Ukážte, že
množina 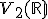 spolu s operáciami
spolu s operáciami 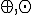 je 2-rozmerný vektorový priestor. Nájdite aspoň jednu jeho bázu.
je 2-rozmerný vektorový priestor. Nájdite aspoň jednu jeho bázu.
Majme množinu
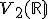 všetkých usporiadaných dvojíc reálnych čísel a operácie:
všetkých usporiadaných dvojíc reálnych čísel a operácie:
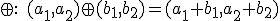 - sčítanie po zložkách.
- sčítanie po zložkách.
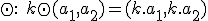 - násobenie skalárom
- násobenie skalárom 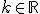 ,
,
kde
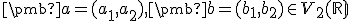 sú ľubovoľné usporiadané dvojice reálnych čísel. Ukážte, že
množina
sú ľubovoľné usporiadané dvojice reálnych čísel. Ukážte, že
množina 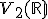 spolu s operáciami
spolu s operáciami 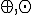 je 2-rozmerný vektorový priestor. Nájdite aspoň jednu jeho bázu.
je 2-rozmerný vektorový priestor. Nájdite aspoň jednu jeho bázu.
Poznámky.
-
Vektorový priestor
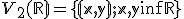 je reprezentovaný množinou všetkých orientovaných úsečiek,
ktoré sú určené ľubovoľnou usporiadanou dvojicou bodov v klasickej euklidovskej rovine.
je reprezentovaný množinou všetkých orientovaných úsečiek,
ktoré sú určené ľubovoľnou usporiadanou dvojicou bodov v klasickej euklidovskej rovine. -
Ak využijeme pravouhlý súradnicový systém s osami
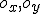 a počiatkom
a počiatkom 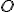 , tak jedno z umiestnení
vektora
, tak jedno z umiestnení
vektora 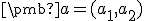 môžeme znázorniť ako orientovanú úsečku
môžeme znázorniť ako orientovanú úsečku 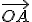 , kde bod
, kde bod 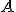 má
súradnice
má
súradnice ![\small [a_1, a_2] \small [a_1, a_2]](https://lms.umb.sk/filter/tex/pix.php/a8c5e147880c19b717c06f75af48db7b.png) . Všimnite si, že budeme rozlišovať zápis usporiadanej dvojice (okrúhle zátvorky) a súradnice bodu v
rovine (hranaté zátvorky).
. Všimnite si, že budeme rozlišovať zápis usporiadanej dvojice (okrúhle zátvorky) a súradnice bodu v
rovine (hranaté zátvorky). - V stredoškolskej matematike sa vektor priamo definuje ako orientovaná úsečka so šípkou smerujúcou od počiatku
![\small [0, 0] \small [0, 0]](https://lms.umb.sk/filter/tex/pix.php/387fd1febbdc2a38e9bb571f79ffc7ae.png) súradnicového systému k
bodu
súradnicového systému k
bodu ![\small [a_1, a_2] \small [a_1, a_2]](https://lms.umb.sk/filter/tex/pix.php/0289645246eb3d04427ee645350dd26c.png) . Šípkou sa označuje “orientácia” vektora
. Šípkou sa označuje “orientácia” vektora 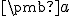 .
. - V písomnom texte budeme vektor
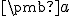 označovať symbolom
označovať symbolom 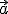 .
.
V pravouhlom súradnicovom systéme usporiadané dvojice 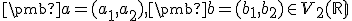 reprezentujú tiež dva
body
reprezentujú tiež dva
body 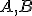 v euklidovskej rovine. Označme
v euklidovskej rovine. Označme 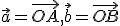 . Potom vektor
. Potom vektor 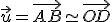 je zrejme súčtom vektorov
je zrejme súčtom vektorov 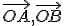 . Toto tvrdenie vyplýva zo zhodnosti trojuholníkov
. Toto tvrdenie vyplýva zo zhodnosti trojuholníkov 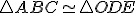 .
Súradnice vektora
.
Súradnice vektora 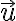 určeného orientovanou úsečkou
určeného orientovanou úsečkou 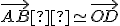 , kde
, kde ![\small A = [a_1, a_2], B = [b_1, b_2] \small A = [a_1, a_2], B = [b_1, b_2]](https://lms.umb.sk/filter/tex/pix.php/722953470976b26fb531d9b2cc406b86.png) určíme ako rozdiely súradníc bodov
určíme ako rozdiely súradníc bodov 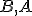 tj.
tj. 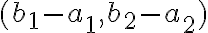 . Vytvorili sme operáciu: odčítavanie bodov, pričom:
. Vytvorili sme operáciu: odčítavanie bodov, pričom:
Rozdielom dvoch bodov je vektor.
Vektor určený orientovanou úsečkou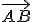 môžeme zapísať aj ako
môžeme zapísať aj ako 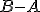 .
.
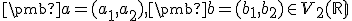 reprezentujú tiež dva
body
reprezentujú tiež dva
body 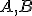 v euklidovskej rovine. Označme
v euklidovskej rovine. Označme 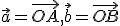 . Potom vektor
. Potom vektor 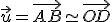 je zrejme súčtom vektorov
je zrejme súčtom vektorov 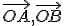 . Toto tvrdenie vyplýva zo zhodnosti trojuholníkov
. Toto tvrdenie vyplýva zo zhodnosti trojuholníkov 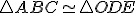 .
Súradnice vektora
.
Súradnice vektora 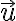 určeného orientovanou úsečkou
určeného orientovanou úsečkou 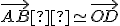 , kde
, kde ![\small A = [a_1, a_2], B = [b_1, b_2] \small A = [a_1, a_2], B = [b_1, b_2]](https://lms.umb.sk/filter/tex/pix.php/722953470976b26fb531d9b2cc406b86.png) určíme ako rozdiely súradníc bodov
určíme ako rozdiely súradníc bodov 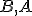 tj.
tj. 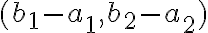 . Vytvorili sme operáciu: odčítavanie bodov, pričom:
. Vytvorili sme operáciu: odčítavanie bodov, pričom:
Rozdielom dvoch bodov je vektor.
Vektor určený orientovanou úsečkou
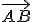 môžeme zapísať aj ako
môžeme zapísať aj ako 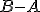 .
.
Cvičenie.
Daný je vektorový priestor
![\small W=[(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)]⊂\mathbb{\pmb Z^4_7} \small W=[(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)]⊂\mathbb{\pmb Z^4_7}](https://lms.umb.sk/filter/tex/pix.php/bd3b10ee76d3e4560ca9d4c3613b338e.png) .
.
Nájdite nejakú bázu priestoru
priestoru 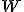 a určite jeho dimenziu, ak
a určite jeho dimenziu, ak
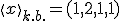 .
.
Priestor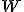 obsahuje štvorice prvkov telesa
obsahuje štvorice prvkov telesa 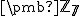 zvyškových tried modulo 7.
zvyškových tried modulo 7.
Daný je vektorový priestor
![\small W=[(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)]⊂\mathbb{\pmb Z^4_7} \small W=[(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)]⊂\mathbb{\pmb Z^4_7}](https://lms.umb.sk/filter/tex/pix.php/bd3b10ee76d3e4560ca9d4c3613b338e.png) .
.
Nájdite nejakú bázu
 priestoru
priestoru 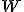 a určite jeho dimenziu, ak
a určite jeho dimenziu, ak
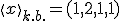 .
.
Priestor
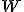 obsahuje štvorice prvkov telesa
obsahuje štvorice prvkov telesa 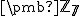 zvyškových tried modulo 7.
zvyškových tried modulo 7.
Poznámka k cvičeniu.
Zápis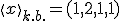 hovorí, že súradnice vektora
hovorí, že súradnice vektora 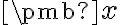 voči kanonickej báze sú
voči kanonickej báze sú 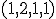 .
Súradnice vektora
.
Súradnice vektora 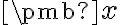 voči kanonickej báze sú koeficienty lineárnej kombinácie vektorov kanonickej bázy dávajúcej vektor
voči kanonickej báze sú koeficienty lineárnej kombinácie vektorov kanonickej bázy dávajúcej vektor 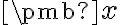 , tj.
, tj.
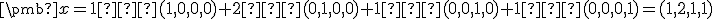 .
.
Súradnice vektora voči kanonickej báze predstavujú priamo zložky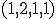 vektora
vektora 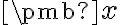 .
.
Zápis
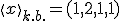 hovorí, že súradnice vektora
hovorí, že súradnice vektora 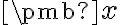 voči kanonickej báze sú
voči kanonickej báze sú 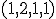 .
Súradnice vektora
.
Súradnice vektora 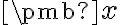 voči kanonickej báze sú koeficienty lineárnej kombinácie vektorov kanonickej bázy dávajúcej vektor
voči kanonickej báze sú koeficienty lineárnej kombinácie vektorov kanonickej bázy dávajúcej vektor 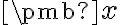 , tj.
, tj.
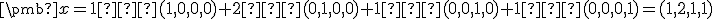 .
.
Súradnice vektora voči kanonickej báze predstavujú priamo zložky
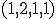 vektora
vektora 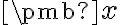 .
.
Riešenie.
- Máme nájsť bázu vektorového priestoru
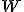 , ktorý je daný ako lineárny obal množiny generátorov
, ktorý je daný ako lineárny obal množiny generátorov
![\small [(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)] \small [(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)]](https://lms.umb.sk/filter/tex/pix.php/d31c0a1c182e55949ca3d63120bfc751.png) .
.
Aby množina vektorov bola bázou, musí byť ešte lineárne nezávislá. - Ak teda nájdeme bázu
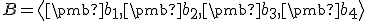 musí pre súradnice vektora
musí pre súradnice vektora 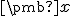 platiť
platiť
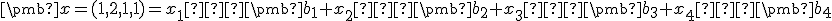 .
.
Z tejto vektorovej rovnice vypočítame súradnice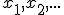 . Najskôr treba upraviť maticu
. Najskôr treba upraviť maticu
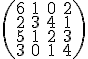
na trojuholníkový tvar (Pozor, pracujeme nad telesom resp. poľom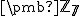 zvyškových tried modulo 7!)
Po prvej iterácii
zvyškových tried modulo 7!)
Po prvej iterácii 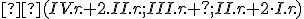 dostanme
dostanme
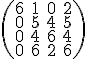 .
.
Urobte ešte dve iterácie tak, aby ste dostali maticu
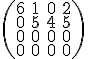 .
.
- Hodnosť matice je rovná 2, preto pre lineárny obal platí
![\small [(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)] =[(6,1,0,2),(0,5,4,5)] \small [(6,1,0,2),(2,3,4,1),(5,1,2,3),(3,0,1,4)] =[(6,1,0,2),(0,5,4,5)]](https://lms.umb.sk/filter/tex/pix.php/68e5861d87aae11fa845fd68ef4e5232.png) .
.
Dimenzia je rovná 2 a aspoň jedna báza je určená lineárne nezávislou množinou vektorov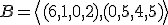
- Určte súradnice vektora
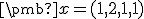 v tejto báze. Výpočet súradníc nájdete Tu.
v tejto báze. Výpočet súradníc nájdete Tu.
Veta - existencia bázy.
Každý netriviálny konečno generovaný vektorový priestor má aspoň jednu konečnú bázu.
Každý netriviálny konečno generovaný vektorový priestor má aspoň jednu konečnú bázu.
Z vlastností hodnosti matíc ľahko odvodíme tvrdenie. Dôkaz nájdete napríklad v práci [Hasek:Linearni algebra a geometrie, str. 45-46].