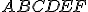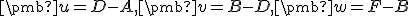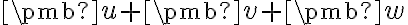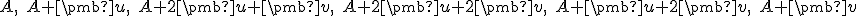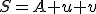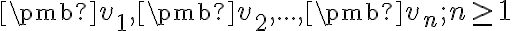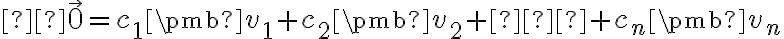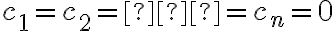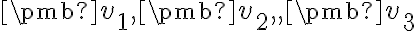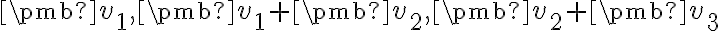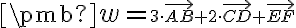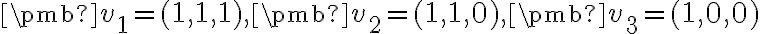Vektorový a afinný priestor
Vektorový priestor
Lineárna závislosť vektorov
V predchádzajúcej kapitole sme pri definícii vektorového priestoru uviedli, že dvojica 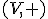 je Abelova komutatívna grupa.
To znamená, že binárna operácia "+" je komutatívna a asociatívna. Zároveň sme definovali násobenie skalárom.
Pomocou týchto dvoch operácií pripomenieme pojmy: lineárna kombinácia, závislosť a nezávislosť vektorov, ktoré sú dôležité a potrebné pri geometrickej manipulácii s vektormi.
je Abelova komutatívna grupa.
To znamená, že binárna operácia "+" je komutatívna a asociatívna. Zároveň sme definovali násobenie skalárom.
Pomocou týchto dvoch operácií pripomenieme pojmy: lineárna kombinácia, závislosť a nezávislosť vektorov, ktoré sú dôležité a potrebné pri geometrickej manipulácii s vektormi.
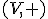 je Abelova komutatívna grupa.
To znamená, že binárna operácia "+" je komutatívna a asociatívna. Zároveň sme definovali násobenie skalárom.
Pomocou týchto dvoch operácií pripomenieme pojmy: lineárna kombinácia, závislosť a nezávislosť vektorov, ktoré sú dôležité a potrebné pri geometrickej manipulácii s vektormi.
je Abelova komutatívna grupa.
To znamená, že binárna operácia "+" je komutatívna a asociatívna. Zároveň sme definovali násobenie skalárom.
Pomocou týchto dvoch operácií pripomenieme pojmy: lineárna kombinácia, závislosť a nezávislosť vektorov, ktoré sú dôležité a potrebné pri geometrickej manipulácii s vektormi.
Lineárna kombinácia.
Nech je daných vektorov
vektorov 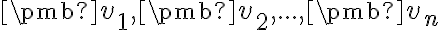 . Každý vektor
. Každý vektor 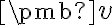 vyjadrený v tvare
vyjadrený v tvare 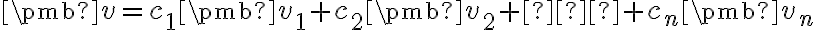 , kde
, kde 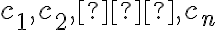 sú reálne čísla, sa nazýva lineárna kombinácia vektorov
sú reálne čísla, sa nazýva lineárna kombinácia vektorov 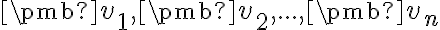 .
.
Nech je daných
 vektorov
vektorov 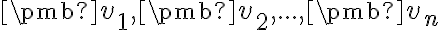 . Každý vektor
. Každý vektor 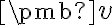 vyjadrený v tvare
vyjadrený v tvare 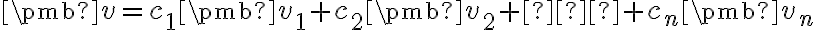 , kde
, kde 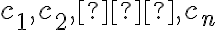 sú reálne čísla, sa nazýva lineárna kombinácia vektorov
sú reálne čísla, sa nazýva lineárna kombinácia vektorov 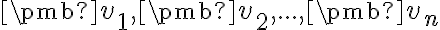 .
.
Príklady.
Lineárna závislosť.
Vektory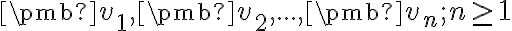 voláme lineárne závislé, ak rovnica
voláme lineárne závislé, ak rovnica
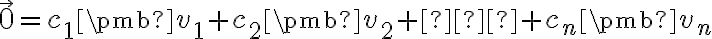
je splnená tak, že aspoň jedno z čísel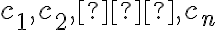 je rôzne od nuly.
je rôzne od nuly.
Vektory
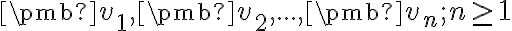 voláme lineárne závislé, ak rovnica
voláme lineárne závislé, ak rovnica
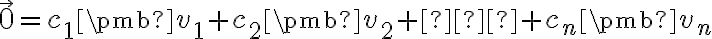
je splnená tak, že aspoň jedno z čísel
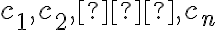 je rôzne od nuly.
je rôzne od nuly.
Príklady.
Po zavedení pojmov lineárna závislosť a lineárna nezávislosť môžeme pristúpiť k pojmom dimenzia a báza vektorového priestoru. Predtým musíme zadefinovať lineárny obal  vektorov a pridať niektoré vektorové axiómy. V ďalšom budeme uvažovať vektorový priestor
vektorov a pridať niektoré vektorové axiómy. V ďalšom budeme uvažovať vektorový priestor 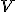 nad telesom
nad telesom 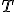 .
.
 vektorov a pridať niektoré vektorové axiómy. V ďalšom budeme uvažovať vektorový priestor
vektorov a pridať niektoré vektorové axiómy. V ďalšom budeme uvažovať vektorový priestor 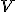 nad telesom
nad telesom 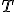 .
.
Definícia.
Nech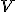 je vektorový priestor nad telesom
je vektorový priestor nad telesom 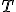 a nech sú dané vektory
a nech sú dané vektory 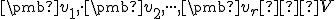 . Potom množinu všetkých vektorov
. Potom množinu všetkých vektorov
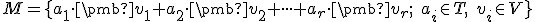
nazývame lineárny obal vektorov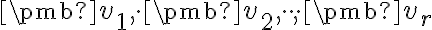 alebo podpriestor
generovaný vektormi
alebo podpriestor
generovaný vektormi 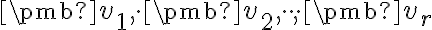 .
Označujeme ho
.
Označujeme ho
![\small M =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb] \small M =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb]](https://lms.umb.sk/filter/tex/pix.php/5789dac5155440696772163cb4343bad.png) .
.
Ak platí![\small \pmb[\pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb ]= V \small \pmb[\pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb ]= V](https://lms.umb.sk/filter/tex/pix.php/355f904d1a775cad94eb0c3b2418a0ca.png) , hovoríme, že vektory
, hovoríme, že vektory 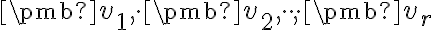 generujú vektorový priestor
generujú vektorový priestor 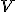 .
.
Nech
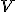 je vektorový priestor nad telesom
je vektorový priestor nad telesom 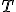 a nech sú dané vektory
a nech sú dané vektory 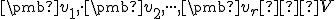 . Potom množinu všetkých vektorov
. Potom množinu všetkých vektorov
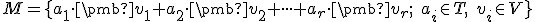
nazývame lineárny obal vektorov
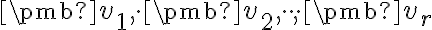 alebo podpriestor
generovaný vektormi
alebo podpriestor
generovaný vektormi 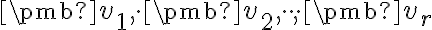 .
Označujeme ho
.
Označujeme ho
![\small M =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb] \small M =: \pmb[ \pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb]](https://lms.umb.sk/filter/tex/pix.php/5789dac5155440696772163cb4343bad.png) .
.
Ak platí
![\small \pmb[\pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb ]= V \small \pmb[\pmb {v_1} , \cdot \pmb {v_2}, \cdot \cdot \cdot, \pmb {v_r}\pmb ]= V](https://lms.umb.sk/filter/tex/pix.php/355f904d1a775cad94eb0c3b2418a0ca.png) , hovoríme, že vektory
, hovoríme, že vektory 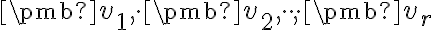 generujú vektorový priestor
generujú vektorový priestor 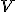 .
.
Cvičenie.
-
Zistite, či vektor
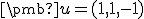 patrí do lineárneho obalu množiny
patrí do lineárneho obalu množiny 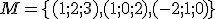 .
.
Dokážte, že ľubovoľný vektor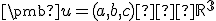 leží v lineárnom obale množiny
leží v lineárnom obale množiny 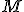 pre ľubovoľnú trojicu
pre ľubovoľnú trojicu 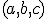 reálnych čísel.
reálnych čísel. -
Je daná množina
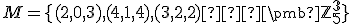 . Rozhodnite, či je vektor
. Rozhodnite, či je vektor 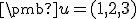 prvkom lineárneho
obalu množiny
prvkom lineárneho
obalu množiny  .
.
Množina obsahuje trojice prvkov telesa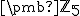 zvyškových tried modulo 5.
zvyškových tried modulo 5. -
Zistite, či vektor
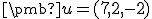 patrí do lineárneho obalu množiny
patrí do lineárneho obalu množiny 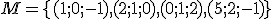 . Ďalšie úlohy na Tu.
. Ďalšie úlohy na Tu.
Riešenie
Cvičenie 1
Hľadajme koeficienty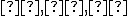 , pre ktoré platí rovnosť
, pre ktoré platí rovnosť
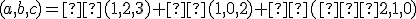 .
.
Po úprave a porovnaní jednotlivých zložiek dostávame sústavu
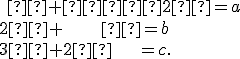
Napríklad Gaussovou eliminačnou metódou zistíme, že sústava má riešenie pre všetky . Nájdite toto riešenie. Pozrite si prácu [Olšák, str. 24].
. Nájdite toto riešenie. Pozrite si prácu [Olšák, str. 24].
Cvičenie 2
Cvičenie 1
Hľadajme koeficienty
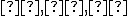 , pre ktoré platí rovnosť
, pre ktoré platí rovnosť
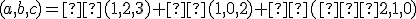 .
.
Po úprave a porovnaní jednotlivých zložiek dostávame sústavu
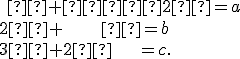
Napríklad Gaussovou eliminačnou metódou zistíme, že sústava má riešenie pre všetky
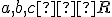 . Nájdite toto riešenie. Pozrite si prácu [Olšák, str. 24].
. Nájdite toto riešenie. Pozrite si prácu [Olšák, str. 24].Cvičenie 2
- Lineárny obal množiny
 priestoru
priestoru 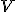 je množina všetkých lineárnych kombinácií vektorov množiny
je množina všetkých lineárnych kombinácií vektorov množiny  s koeficientmi
z poľa. Teda stačí zistiť, či je možné vektor
s koeficientmi
z poľa. Teda stačí zistiť, či je možné vektor 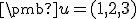 zapísať ako lineárnu kombináciu vektorov množiny
zapísať ako lineárnu kombináciu vektorov množiny  .
. - Vektor
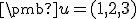 patrí do lineárneho obalu množiny
patrí do lineárneho obalu množiny  ak existujú prvky
ak existujú prvky 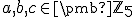 tak, aby
tak, aby
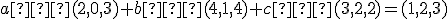 .
.
Pre každú vektorovú zložku získame rovnicu. Trojica nasledujúcich rovníc tvorí sústavu, ktorú vyriešime. Pozor – sústavu riešime nad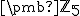 !
!
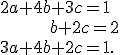 Sčítaním prvej a druhej rovnice dostaneme
Sčítaním prvej a druhej rovnice dostaneme
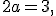
lebo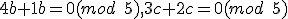 a sčítaním 3.r.+2.r. dostanme
a sčítaním 3.r.+2.r. dostanme
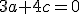
odkiaľ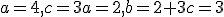 . Sústava má v poli
. Sústava má v poli 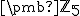 riešenie. Vektor
riešenie. Vektor 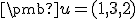 je lineárnou
kombináciou vektorov množiny
je lineárnou
kombináciou vektorov množiny  . Preto
. Preto ![\small \pmb {u} \in [M] \small \pmb {u} \in [M]](https://lms.umb.sk/filter/tex/pix.php/6431c2864e125629b6d107dc96a26489.png) .
.