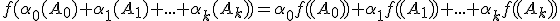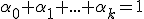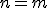Vektorový a afinný priestor
Afinné zobrazenie
V ďalších kapitolách sa budeme zaoberať len euklidovským priestorom 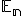 so zameraním
so zameraním 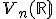 . Zameriame sa prevažne len na dvojrozmerný a trojrozmerný euklidovský priestor - rovinu
. Zameriame sa prevažne len na dvojrozmerný a trojrozmerný euklidovský priestor - rovinu 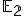 a priestor
a priestor 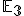 . Pripomíname, že v euklidovskom priestore je definovaný skalárny súčin.
. Pripomíname, že v euklidovskom priestore je definovaný skalárny súčin.
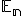 so zameraním
so zameraním 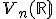 . Zameriame sa prevažne len na dvojrozmerný a trojrozmerný euklidovský priestor - rovinu
. Zameriame sa prevažne len na dvojrozmerný a trojrozmerný euklidovský priestor - rovinu 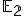 a priestor
a priestor 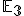 . Pripomíname, že v euklidovskom priestore je definovaný skalárny súčin.
. Pripomíname, že v euklidovskom priestore je definovaný skalárny súčin.
Definícia.
Nech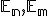 sú euklidovské priestory. Zobrazenie
sú euklidovské priestory. Zobrazenie 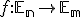 sa nazýva afinné zobrazenie (AZ), ak obrazom ľubovoľných troch kolineárnych bodov sú totožné body, alebo kolineárne body, pričom ich deliaci pomer sa zachováva.
sa nazýva afinné zobrazenie (AZ), ak obrazom ľubovoľných troch kolineárnych bodov sú totožné body, alebo kolineárne body, pričom ich deliaci pomer sa zachováva.
Nech
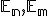 sú euklidovské priestory. Zobrazenie
sú euklidovské priestory. Zobrazenie 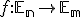 sa nazýva afinné zobrazenie (AZ), ak obrazom ľubovoľných troch kolineárnych bodov sú totožné body, alebo kolineárne body, pričom ich deliaci pomer sa zachováva.
sa nazýva afinné zobrazenie (AZ), ak obrazom ľubovoľných troch kolineárnych bodov sú totožné body, alebo kolineárne body, pričom ich deliaci pomer sa zachováva.
Z definície vyplýva, že afinné zobrazenie má vlastnosť lineárneho zobrazenia.
Dôkaz (urobíme pre 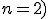
Nech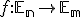 je afinné zobrazenie a nech
je afinné zobrazenie a nech
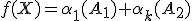 , kde
, kde 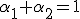 .
Pre ľubovoľný bod
.
Pre ľubovoľný bod 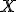 priamky
priamky 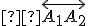 platí
platí
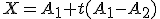
a pre jeho obraz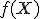 priamky
priamky 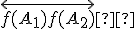 bude
bude
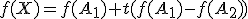
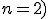
Nech
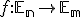 je afinné zobrazenie a nech
je afinné zobrazenie a nech
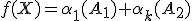 , kde
, kde 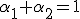 .
Pre ľubovoľný bod
.
Pre ľubovoľný bod 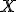 priamky
priamky 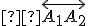 platí
platí
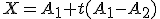
a pre jeho obraz
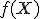 priamky
priamky 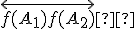 bude
bude
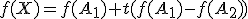
Poznámky.
♥ Príklad Tri body.
Afinné zobrazenie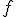 zobrazuje body
zobrazuje body ![\small A[2, 1], B[3, 0], C[1, 4] \small A[2, 1], B[3, 0], C[1, 4]](https://lms.umb.sk/filter/tex/pix.php/3f4645363521a7c7ddf8f031272960e8.png) do bodov
do bodov ![\small A'[1, 6], B'[1, 9], C'[3, 1] \small A'[1, 6], B'[1, 9], C'[3, 1]](https://lms.umb.sk/filter/tex/pix.php/95a78b0e2732eb2134ca3344d270d527.png) v tomto poradí. Kam sa zobrazí bod
v tomto poradí. Kam sa zobrazí bod ![\small P[5, 7] \small P[5, 7]](https://lms.umb.sk/filter/tex/pix.php/12b32440cc18cd0bfb55063d1f30e434.png) resp. bod
resp. bod ![\small X[x, y] \small X[x, y]](https://lms.umb.sk/filter/tex/pix.php/efa1e94429b3777f84985fcc9f922d4c.png) ? Prevzaté z práce (Chalmoviansky, Cvičenie 28).
? Prevzaté z práce (Chalmoviansky, Cvičenie 28).
Afinné zobrazenie
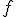 zobrazuje body
zobrazuje body ![\small A[2, 1], B[3, 0], C[1, 4] \small A[2, 1], B[3, 0], C[1, 4]](https://lms.umb.sk/filter/tex/pix.php/3f4645363521a7c7ddf8f031272960e8.png) do bodov
do bodov ![\small A'[1, 6], B'[1, 9], C'[3, 1] \small A'[1, 6], B'[1, 9], C'[3, 1]](https://lms.umb.sk/filter/tex/pix.php/95a78b0e2732eb2134ca3344d270d527.png) v tomto poradí. Kam sa zobrazí bod
v tomto poradí. Kam sa zobrazí bod ![\small P[5, 7] \small P[5, 7]](https://lms.umb.sk/filter/tex/pix.php/12b32440cc18cd0bfb55063d1f30e434.png) resp. bod
resp. bod ![\small X[x, y] \small X[x, y]](https://lms.umb.sk/filter/tex/pix.php/efa1e94429b3777f84985fcc9f922d4c.png) ? Prevzaté z práce (Chalmoviansky, Cvičenie 28).
? Prevzaté z práce (Chalmoviansky, Cvičenie 28).
Riešenie.
Prvý spôsob.
Bod![\small P[5, 7] \small P[5, 7]](https://lms.umb.sk/filter/tex/pix.php/12b32440cc18cd0bfb55063d1f30e434.png) vyjadrime ako lineárnu kombináciu bodov
vyjadrime ako lineárnu kombináciu bodov ![\small A[2, 1], B[3, 0], C[1, 4] \small A[2, 1], B[3, 0], C[1, 4]](https://lms.umb.sk/filter/tex/pix.php/3f4645363521a7c7ddf8f031272960e8.png) . V takom prípade musia existovať reálne čísla
. V takom prípade musia existovať reálne čísla 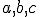
(1)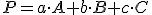
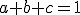 .
.
Zobrazenie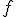 je lineárne, preto pre obraz
je lineárne, preto pre obraz ![\small P'[x',y'] \small P'[x',y']](https://lms.umb.sk/filter/tex/pix.php/c4981cddaf1f66c7b9b1f9ef84c5f482.png) bodu
bodu  bude platiť
bude platiť
(2)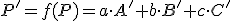 , pričom tiež musí platiť
, pričom tiež musí platiť 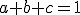
Sústavu rovníc (1) a (2) vyjadríme v maticovom tvare a vyriešime.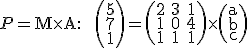
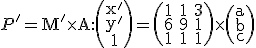
Po vyjadrení
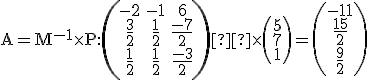
a po dosadení do (2) dostaneme riešenie
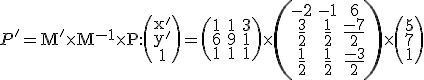 .
.
Po roznásobení
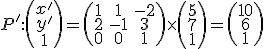 .
.
Porovnaním ľavej a pravej strany dostaneme riešenie![\small P'=[10,6] \small P'=[10,6]](https://lms.umb.sk/filter/tex/pix.php/f4056527435d985bc1a407c62a354369.png) .
.
Prvý spôsob.
Bod
![\small P[5, 7] \small P[5, 7]](https://lms.umb.sk/filter/tex/pix.php/12b32440cc18cd0bfb55063d1f30e434.png) vyjadrime ako lineárnu kombináciu bodov
vyjadrime ako lineárnu kombináciu bodov ![\small A[2, 1], B[3, 0], C[1, 4] \small A[2, 1], B[3, 0], C[1, 4]](https://lms.umb.sk/filter/tex/pix.php/3f4645363521a7c7ddf8f031272960e8.png) . V takom prípade musia existovať reálne čísla
. V takom prípade musia existovať reálne čísla 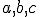
(1)
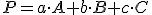
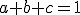 .
.
Zobrazenie
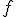 je lineárne, preto pre obraz
je lineárne, preto pre obraz ![\small P'[x',y'] \small P'[x',y']](https://lms.umb.sk/filter/tex/pix.php/c4981cddaf1f66c7b9b1f9ef84c5f482.png) bodu
bodu  bude platiť
bude platiť
(2)
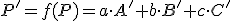 , pričom tiež musí platiť
, pričom tiež musí platiť 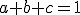
Sústavu rovníc (1) a (2) vyjadríme v maticovom tvare a vyriešime.
Pri násobení matíc typu 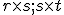 výsledná matica je typu
výsledná matica je typu 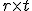 , preto matica
, preto matica  rep.
matica
rep.
matica 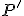 bude typu 3 x 1, pričom prvok
bude typu 3 x 1, pričom prvok 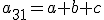 bude zrejme rovný 1. (Pri riešení sme použili kalkulátor
"Matrix calculator", ktorý je dostupný
Tu.
bude zrejme rovný 1. (Pri riešení sme použili kalkulátor
"Matrix calculator", ktorý je dostupný
Tu.
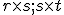 výsledná matica je typu
výsledná matica je typu 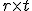 , preto matica
, preto matica  rep.
matica
rep.
matica 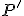 bude typu 3 x 1, pričom prvok
bude typu 3 x 1, pričom prvok 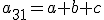 bude zrejme rovný 1. (Pri riešení sme použili kalkulátor
"Matrix calculator", ktorý je dostupný
Tu.
bude zrejme rovný 1. (Pri riešení sme použili kalkulátor
"Matrix calculator", ktorý je dostupný
Tu.
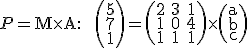
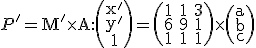
Po vyjadrení
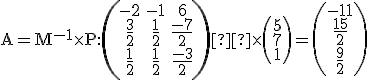
a po dosadení do (2) dostaneme riešenie
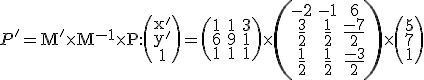 .
.
Po roznásobení
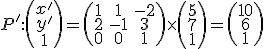 .
.
Porovnaním ľavej a pravej strany dostaneme riešenie
![\small P'=[10,6] \small P'=[10,6]](https://lms.umb.sk/filter/tex/pix.php/f4056527435d985bc1a407c62a354369.png) .
.
Dôsledok.
V našom príklade ak pre bod zvolíme všeobecné súradnice
zvolíme všeobecné súradnice ![\small P=[x,y] \small P=[x,y]](https://lms.umb.sk/filter/tex/pix.php/cb5958c2025b20cde42da0c659bb6c06.png) , tak riešenie môžeme zapísať v tvare
, tak riešenie môžeme zapísať v tvare
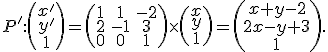
V našom príklade ak pre bod
 zvolíme všeobecné súradnice
zvolíme všeobecné súradnice ![\small P=[x,y] \small P=[x,y]](https://lms.umb.sk/filter/tex/pix.php/cb5958c2025b20cde42da0c659bb6c06.png) , tak riešenie môžeme zapísať v tvare
, tak riešenie môžeme zapísať v tvare
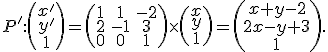
Transfomačné rovnice afinného zobrazenia.
Porovnaním riadkov matíc dostaneme sústavu - transformačné rovnice zobrazenia z príkladu "Tri body"
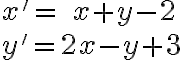
Dosaďte súradnice![\small P[5, 7] \small P[5, 7]](https://lms.umb.sk/filter/tex/pix.php/c41015f970c9b7be85aba7a97ad4bc91.png) do tejto sústavy a zistíte súradnice hľadaného bodu
do tejto sústavy a zistíte súradnice hľadaného bodu ![\small P'[10, 6] \small P'[10, 6]](https://lms.umb.sk/filter/tex/pix.php/90ab42afff53c904fa7219eec0f1751b.png) .
.
Porovnaním riadkov matíc dostaneme sústavu - transformačné rovnice zobrazenia z príkladu "Tri body"
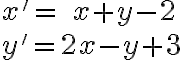
Dosaďte súradnice
![\small P[5, 7] \small P[5, 7]](https://lms.umb.sk/filter/tex/pix.php/c41015f970c9b7be85aba7a97ad4bc91.png) do tejto sústavy a zistíte súradnice hľadaného bodu
do tejto sústavy a zistíte súradnice hľadaného bodu ![\small P'[10, 6] \small P'[10, 6]](https://lms.umb.sk/filter/tex/pix.php/90ab42afff53c904fa7219eec0f1751b.png) .
.
Pozrite si riešenie v GeoGebre
Tu.
Kompletné grafické riešenie pre afinné zobrazenie určené obrazmi troch bodov si stiahnete Tu.
Druhý spôsob riešenia príkladu "Tri body".
Sústavu môžeme riešiť aj dosadením súradníc dostávame![\small [5, 7]=a \cdot [2, 1]+b \cdot [3, 0]+c \cdot [1, 4] \small [5, 7]=a \cdot [2, 1]+b \cdot [3, 0]+c \cdot [1, 4]](https://lms.umb.sk/filter/tex/pix.php/cd188dc3a3f62ee19f485172daac0c7c.png) a po roznásobení dostaneme
sústavu troch rovníc o troch nezámych
a po roznásobení dostaneme
sústavu troch rovníc o troch nezámych
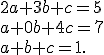
Dostaneme riešenie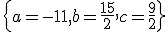 .
.
V afinnom zobrazení sa kolineárnosť zachováva, preto platí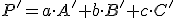 . Po dosadení riešenia a súradníc bodov
. Po dosadení riešenia a súradníc bodov
![\small A'[1, 6], 'B[1, 9], C'[3, 1] \small A'[1, 6], 'B[1, 9], C'[3, 1]](https://lms.umb.sk/filter/tex/pix.php/eaaa2b6f3ad10f9287f3a91a1563eba9.png) dostaneme
dostaneme
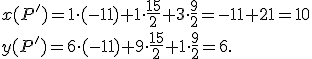
Sústavu môžeme riešiť aj dosadením súradníc dostávame
![\small [5, 7]=a \cdot [2, 1]+b \cdot [3, 0]+c \cdot [1, 4] \small [5, 7]=a \cdot [2, 1]+b \cdot [3, 0]+c \cdot [1, 4]](https://lms.umb.sk/filter/tex/pix.php/cd188dc3a3f62ee19f485172daac0c7c.png) a po roznásobení dostaneme
sústavu troch rovníc o troch nezámych
a po roznásobení dostaneme
sústavu troch rovníc o troch nezámych
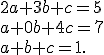
Dostaneme riešenie
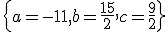 .
.
V afinnom zobrazení sa kolineárnosť zachováva, preto platí
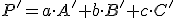 . Po dosadení riešenia a súradníc bodov
. Po dosadení riešenia a súradníc bodov
![\small A'[1, 6], 'B[1, 9], C'[3, 1] \small A'[1, 6], 'B[1, 9], C'[3, 1]](https://lms.umb.sk/filter/tex/pix.php/eaaa2b6f3ad10f9287f3a91a1563eba9.png) dostaneme
dostaneme
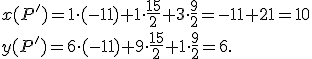
Príklad.
Zobrazenie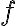 roviny
roviny 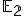 do tej istej roviny, ktoré bodu
do tej istej roviny, ktoré bodu 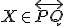 priradí bod
priradí bod 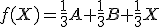 je afinné zobrazenie. Zobrazenie, ktoré trojuholníku s jedným premenným vrcholom
priradí jeho ťažisko je afinné zobrazenie. Pozrite si dôkaz, že takéto zobrazenie je afinné
Tu.
je afinné zobrazenie. Zobrazenie, ktoré trojuholníku s jedným premenným vrcholom
priradí jeho ťažisko je afinné zobrazenie. Pozrite si dôkaz, že takéto zobrazenie je afinné
Tu.
Zobrazenie
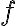 roviny
roviny 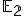 do tej istej roviny, ktoré bodu
do tej istej roviny, ktoré bodu 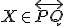 priradí bod
priradí bod 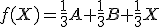 je afinné zobrazenie. Zobrazenie, ktoré trojuholníku s jedným premenným vrcholom
priradí jeho ťažisko je afinné zobrazenie. Pozrite si dôkaz, že takéto zobrazenie je afinné
Tu.
je afinné zobrazenie. Zobrazenie, ktoré trojuholníku s jedným premenným vrcholom
priradí jeho ťažisko je afinné zobrazenie. Pozrite si dôkaz, že takéto zobrazenie je afinné
Tu.