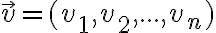Vektorový a afinný priestor
Euklidovský priestor
Vektorový priestor, na ktorom je definovaný skalárny súčin (tiež nazývaný aj vnútorný súčin) umožňuje rozumne definovať geometrické pojmy uhol a vzdialenosť, čím na tomto vektorovom priestore vzniká dodatočná geometrická štruktúra.
Euklidovský priestor je 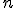 -rozmerný afinný priestor so zameraním
-rozmerný afinný priestor so zameraním 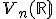 a s vyššie
definovaným skalárnym súčinom; označovať’ ho budeme symbolom
a s vyššie
definovaným skalárnym súčinom; označovať’ ho budeme symbolom 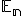 .
.
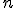 -rozmerný afinný priestor so zameraním
-rozmerný afinný priestor so zameraním 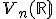 a s vyššie
definovaným skalárnym súčinom; označovať’ ho budeme symbolom
a s vyššie
definovaným skalárnym súčinom; označovať’ ho budeme symbolom 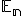 .
.
Vo vektorovom priestore okrem skalárneho súčinu, ktorého výsledkom je skalár (reálne číslo), môžeme definovať operáciu, ktorej výsledkom bude
vektor kolmý na obidva pôvodné vektory. Pre vektorový súčin uvedieme definíciu pomocou zobrazenie, ktoré dvojici vektorov v trojrozmernom Euklidovskom
priestore priraďuje vektor kolmý na obidva pôvodné vektory.
Definícia - vektorový súčin.
Vektorový súčin dvoch vektorov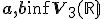 je definovaný ako vektor kolmý k vektorom
je definovaný ako vektor kolmý k vektorom 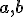 , ktorého veľkosť
je rovná ploche kosodĺžnika, ktorý oba vektory vytvárajú. Zapisujeme
, ktorého veľkosť
je rovná ploche kosodĺžnika, ktorý oba vektory vytvárajú. Zapisujeme
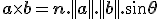 ,
,
kde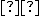 je uhol zvieraný vektormi
je uhol zvieraný vektormi 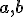 s vlastnosťou
s vlastnosťou 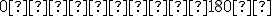 a
a 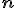 je jednotkový
vektor kolmý k nim.
je jednotkový
vektor kolmý k nim.
Vektorový súčin dvoch vektorov
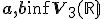 je definovaný ako vektor kolmý k vektorom
je definovaný ako vektor kolmý k vektorom 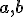 , ktorého veľkosť
je rovná ploche kosodĺžnika, ktorý oba vektory vytvárajú. Zapisujeme
, ktorého veľkosť
je rovná ploche kosodĺžnika, ktorý oba vektory vytvárajú. Zapisujeme
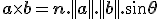 ,
,
kde
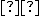 je uhol zvieraný vektormi
je uhol zvieraný vektormi 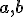 s vlastnosťou
s vlastnosťou 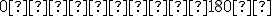 a
a 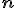 je jednotkový
vektor kolmý k nim.
je jednotkový
vektor kolmý k nim.
Veta.
Vektorový súčin možno definovať aj bez pomoci uhla, ktorý oba vektory určujú. Nech sú dané vektory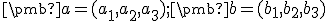 . Potom
zložky vektora
. Potom
zložky vektora  vektorového súčinu
vektorového súčinu 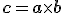 možno určiť ako
možno určiť ako
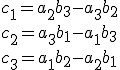 .
.
Vektorový súčin možno definovať aj bez pomoci uhla, ktorý oba vektory určujú. Nech sú dané vektory
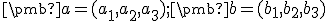 . Potom
zložky vektora
. Potom
zložky vektora  vektorového súčinu
vektorového súčinu 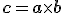 možno určiť ako
možno určiť ako
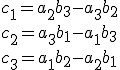 .
.
Pomôcka na výpočet súradníc vektora  .
.
Zapíšeme si súradnice vektorov do zákrytov pod seba, prvý riadok budú súradnice vektora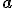 a pridáme ešte raz jeho
prvú a druhú súradnicu. V druhom riadku urobím to isté s vektorom
a pridáme ešte raz jeho
prvú a druhú súradnicu. V druhom riadku urobím to isté s vektorom 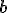 . Dostaneme schému
. Dostaneme schému
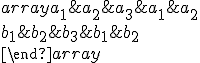 .
.
Teraz určíme súradnice vektora - krížové násobenie:
- krížové násobenie: 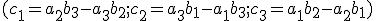 .
.
 .
.
Zapíšeme si súradnice vektorov do zákrytov pod seba, prvý riadok budú súradnice vektora
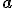 a pridáme ešte raz jeho
prvú a druhú súradnicu. V druhom riadku urobím to isté s vektorom
a pridáme ešte raz jeho
prvú a druhú súradnicu. V druhom riadku urobím to isté s vektorom 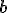 . Dostaneme schému
. Dostaneme schému
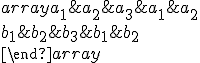 .
.
Teraz určíme súradnice vektora
 - krížové násobenie:
- krížové násobenie: 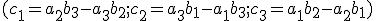 .
.
Poznámky.
- Pre obsah trojuholníka
 je známy vzorec
je známy vzorec 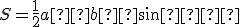 , kde
, kde 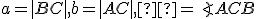 . Porovnaním s definíciou
vektorového súčinu, môžeme písať
. Porovnaním s definíciou
vektorového súčinu, môžeme písať 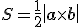 .
.
- Pomocou zmiešaného súčinu troch vektorov môžeme vypočítať objem rovnobežnostena. Pozrite si prácu Vodičková, V.: Aplikácie vektorového súčinu. Dostupné Tu.
Cvičenie.
Riešenie.
- ...
- ...
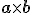
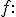
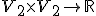
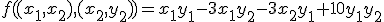
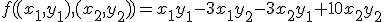
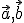
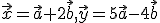
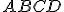
![\small A[5; 1; 4], B[−1; −2; 6], C[2; 3; −2] \small A[5; 1; 4], B[−1; −2; 6], C[2; 3; −2]](https://lms.umb.sk/filter/tex/pix.php/19ed960c9979573457cd0ef9b18a7051.png)
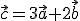
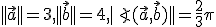
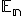
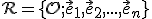
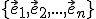
![\small X[x_1, x_2, . . . , x_n] \small X[x_1, x_2, . . . , x_n]](https://lms.umb.sk/filter/tex/pix.php/eba92bf93a3de0a9032b7ed7172dbbd8.png)