Predchádzajúci
Nasledujúci
V Euklidových Základoch sú uvedené prvé dve tvrdenia (symbolicky T/I a T/II), ktoré sa týkajúce existencie rovnostranného trojuholníka a "prenášania" úsečky do polohy s daným počiatočným bodom. Euklides dokazuje tieto tvrdenia formou konštrukcie resp. návodov ako postupovať pri dokazovaní týchto tvrdení.
V dôkaze T/II sa používa niečo ako pohyb, ale v skutočnosti sa tam nič nepohybuje.
Tvrdenia
  1. T/I: Vytvoriť rovnostranný trojuholník na danej konečnej priamke. Celé tvrdenie resp. celú konštrukciu nájdete Tu.
  2. T/II: Z daného bodu 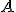\small A narysovať úsečku 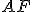\small AF zhodnú s danou úsečkou \small BC .
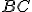Dôkaz tvrdenia T/II prezentujeme vo forme dynamickej konštrukcie - appletu v programe GeoGebra.


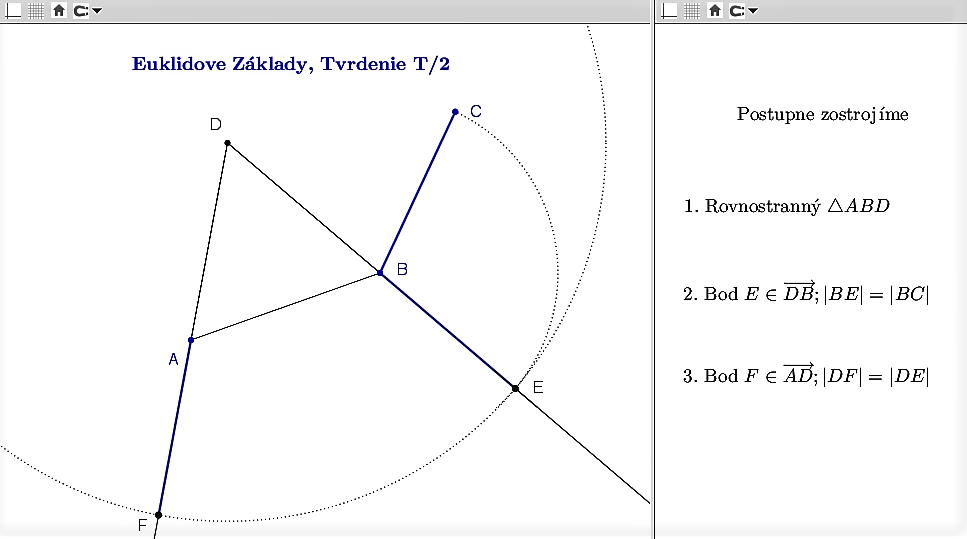
Applet si otvoríte programom GeoGebra Tu.
Poznámky
  1. Pri dokazovaní týchto prvých dvoch tvrdení Euklides využíva prvý postulát o existencii priamky určenej dvoma bodmi.
      • Z hľadiska konštruovateľnosti tento postulát predstavuje existenciu pravítka.
  2. Zároveň využíva tretí postulát o možnosti zostrojenia kruhu určeného stredom a polomerom.
      • Z hľadiska konštruovateľnosti to môžeme považovať za existenciu kružidla.
Definícia kruhu intuitívne používa pojmy "medzi" a "zhodnosť", ktoré nie sú v Základoch zavedené. Neskôr (takmer o dve tisíc rokov) tieto pojmy zavádza Hilbert vo svojom axiomatickom systéme, kde sa kružnica po uvedení axióm zhodnosti už môže zadefinovať.
Euklides v dôkazoch predpokladá, že pri prenášaní úsečky sa jej veľkosť nezmení. Toto v Hilbertovej sústave zabezpečujú axiómy zhodnosti.
Euklidovská konštrukcia sa nazýva grafická konštrukcia v euklidovskom priestore realizovaná
  1. ideálnym pravítkom a ideálnym kružidlom
  2. konečným počtom krokov
  3. každý krok je elementárna konštrukcia na zostrojenie
    1. priamky prechádzajúcej dvoma danými rôznymi bodmi
    2. kružnice so stredom v danom bode a s daným polomerom
    3. priesečníka dvoch rôznobežných priamok (resp. prieniku priamky a kružnice alebo prieniku dvoch kružníc).
Elementárne euklidovské konštrukcie
  1. Zostrojenie stredu danej úsečky.
  2. Zostrojenie osi úsečky, osi daného uhla.
  3. "Prenesenie" danej úsečky na danú polpriamku. Tvrdenie T/III.
  4. "Prenesenie" daného uhla na danú polpriamku v danej polrovine.
Poznámky
  1. V euklidovskej rovine prvé dve uvedené elementárne konštrukcie nie problém zrealizovať, ak máme k dispozícii pravítko a kružidlo. Pozrite si konštrukciu Tu.
  2. V geometrii, v ktorej neplatí piaty Euklidov postulát (neeuklidovské geometrie) to také jednoduché nebude. V prvom rade musíme nájsť odpoveď na otázku: "Čo budeme rozumieť pod pravítkom resp. kružidlom v takejto geometrii?"
  3. V ďalšej časti sa pokúsime zodpovedať na túto otázku a následne vytvoriť elementárne euklidovské konštrukcie v neeuklidovskej geometrii.
\( .\)
Predchádzajúci
Nasledujúci