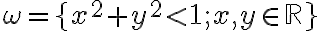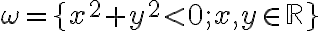Neeuklidovská geometria euklidovsky
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Neeuklidovská geometria euklidovsky |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 13:42 |
Abstrakt
V príspevku sa zaoberáme axiomatickým systémom rovinnej geometrie, ktorý bol navrhnutý Euklidom a neskôr upravený Hilbertom. Ťažiskom práce je model Poincaré Disc neeuklidovskej roviny. Navrhnuté sú nástroje v programe GeoGebra pre Poincaré Disc - hPriamka a hKružnica a z nich ďalšie špecificky odvodené nástroje. Riešené sú základné euklidovské konštrukcie v modeli Poincaré Disc.
Kľúčové slová: Euklidove Základy, hyperbolická geometria, Poincaré Disc, GeoGebra nástroje
Abstract
In the work, we develop the axiomatic system of plane geometry, which was proposed by Euclid and later modified by Hilbert. The focus of the work is the Poincaré Disc model of the non-Euclidean plane. The tools in the GeoGebra program are designed for the Poincaré Disc - hLine and hCircle and other specific tools. Solved basic Euclidean constructions in the Poincaré Disc model.
Keywords: Euclidean Elements, hyperbolic geometry, Poincaré Disc, GeoGebra tools
V príspevku sa zaoberáme axiomatickým systémom rovinnej geometrie, ktorý bol navrhnutý Euklidom a neskôr upravený Hilbertom. Ťažiskom práce je model Poincaré Disc neeuklidovskej roviny. Navrhnuté sú nástroje v programe GeoGebra pre Poincaré Disc - hPriamka a hKružnica a z nich ďalšie špecificky odvodené nástroje. Riešené sú základné euklidovské konštrukcie v modeli Poincaré Disc.
Kľúčové slová: Euklidove Základy, hyperbolická geometria, Poincaré Disc, GeoGebra nástroje
Abstract
In the work, we develop the axiomatic system of plane geometry, which was proposed by Euclid and later modified by Hilbert. The focus of the work is the Poincaré Disc model of the non-Euclidean plane. The tools in the GeoGebra program are designed for the Poincaré Disc - hLine and hCircle and other specific tools. Solved basic Euclidean constructions in the Poincaré Disc model.
Keywords: Euclidean Elements, hyperbolic geometry, Poincaré Disc, GeoGebra tools
V historickom vývoji geometrie nájdeme dva východiskové míľniky, ktoré by sme mohli charakterizovať tromi otázkami:
„Ako to vytvoriť? “
„Prečo to platí?“
„Platí piaty Euklidov postulát?“
Pozrite si práce [GRE], [VAL].
„Ako to vytvoriť? “
„Prečo to platí?“
„Platí piaty Euklidov postulát?“
Pozrite si práce [GRE], [VAL].
- Začiatok tejto cesty „Ako “ patrí približne do obdobia dvoch tisícročí pred naším letopočtom, do obdobia mezopotámskeho a egyptského staroveku.
- Obdobie „Prečo“ zahŕňa obdobie od antického Grécka (Tháles, Pytagoras, Euklides) až po objavy neeuklidovských geometrií. S úctou k velikánom gréckej matematiky a filozofie treba zdôrazniť, že mnohé grécke myšlienky predbehli svoju dobu o dve nasledujúce tisícročia.
Objav neeuklidovských geometrií1) v 19. storočí patrí k najvýznamnejším historickým etapám vo vývoji matematiky a mal hlboký vplyv na vedu a filozofiu. Slovami M. Greenberga (pozrite si prácu [GRE]):
„Väčšina ľudí nevie, že v 19. storočí došlo k revolúcii v oblasti geometrie, ktorá bola vedecky tak hlboká a
vo svojom vplyve rovnako filozoficky dôležitá ako Darwinova evolučná teória.“
Prenikaním informačno-komunikačných technológií (IKT) do života spoločnosti koncom 20. storočia nášho letopočtu sa začala revolúcia nielen v myslení ľudí ale aj v organizácii a riadení ich práce. Používanie IKT vo vzdelávacom procese sa stalo neodmysliteľnou súčasťou moderného vyučovania.
___________________________________________________________________________
1) Vynechanie piateho Euklidovho postulátu z axiomatického systému výstavby geometrie.
1) Vynechanie piateho Euklidovho postulátu z axiomatického systému výstavby geometrie.
Slovo geometria pochádza z gréckeho výrazu hé gé meteón, čo znamená vymeriavanie pozemkov pomocou lán. Pozri prácu [SED]. Matematika ako veda vznikla v Grécku približne v období 6. - 5. st. pred n. l.
Základy geometrie nachádzame už v Babylone, Egypte, Indii a Číne. Veľký rozmach zaznamenala grécka matematika, ktorá nám zanechala dielo nesmiernej hodnoty - Euklidove Základy.
Gréci boli prví, ktorí začali matematické tvrdenia dokazovať, pričom používali deduktívnu metódu.
Gréci ako prví prestali riešiť iba otázku ako, ale hľadali aj odpovede na otázku prečo.
Významní predstavitelia gréckej matematiky: Tháles, Pytagoras, Euklides, Archimedes.
Gréci ako prví prestali riešiť iba otázku ako, ale hľadali aj odpovede na otázku prečo.
Významní predstavitelia gréckej matematiky: Tháles, Pytagoras, Euklides, Archimedes.
V starom Grécku bol popísaný systém základných geometrických pojmov a vzťahov medzi nimi -
postulátov.
Takýto kompletne spracovaný systém bol publikovaný v Euklidových Základoch. Pozrite si práce [EUC] a [SER]. Toto dielo sa považuje za základy planimetrie, stereometrie a geometrickej algebry.
Český preklad Euklidových Základov od Františka Servíta si môžete stiahnuť Tu. Existuje aj anglická elektronická verzia Tu.
Takýto kompletne spracovaný systém bol publikovaný v Euklidových Základoch. Pozrite si práce [EUC] a [SER]. Toto dielo sa považuje za základy planimetrie, stereometrie a geometrickej algebry.
Český preklad Euklidových Základov od Františka Servíta si môžete stiahnuť Tu. Existuje aj anglická elektronická verzia Tu.
V roku 1899 slávny matematik David Hilbert publikoval prácu Grundlagen der Geometrie, v ktorej navrhuje axiomatický systém, nahrádzajúci tradičné axiómy Euklida.
V práci [HIL] sa uvádza šesť primitívnych pojmov. Tieto pojmy sú začlenené do dvoch skupín:
- Primitívne objekty
- body - označujeme veľkými písmenami latinskej abecedy
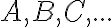 ;
; - priamky - na označenie používame malé písmená
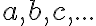 a
a - roviny - označujeme malými gréckymi písmenami
 .
. - Primitívne vzťahy (binárne relácie)
- incidencia -
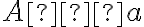 ["bod
["bod
 leží na priamke
leží na priamke  ", "priamka
", "priamka  prechádza bodom
prechádza bodom
 ", "bod
", "bod
 a priamka
a priamka  sú incidentné"].
sú incidentné"]. - vzťah "medzi" -
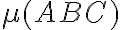 [usporiadanie troch kolineárnych bodov
[usporiadanie troch kolineárnych bodov
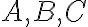 , kde bod
, kde bod
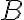 leží medzi bodmi
leží medzi bodmi
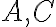 ]; používa sa aj označenie
]; používa sa aj označenie 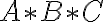 . Pozri prácu [CHAL].
. Pozri prácu [CHAL]. - zhodnosť (kongruencia) -
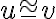 ["úsečka
["úsečka  je zhodná s úsečkou
je zhodná s úsečkou 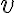 "], zhodnosť uhlov, zhodnosť trojuholníkov.
"], zhodnosť uhlov, zhodnosť trojuholníkov.
Primitívne objekty nedefinujeme, vieme však jednoznačne rozhodnúť o vzťahoch medzi nimi. Interpretáciu primitívnych vzťahov reprezentuje nasledujúci applet, ktorý si aktivujete
Tu.

Hilbertov axiomatický systém pozostáva z piatich skupín axióm.
- axiómy incidencie
- axiómy usporiadania
- axiómy zhodnosti (kongruencie)
- axióma o rovnobežnosti
- axiómy spojitosti Axiómy charakterizujú vzťahy medzi primitívnymi objektmi. Axiomatický systém obsahuje celkom 20 axióm.
Viac o Hilbertovom axiomatickom systéme nájde čitateľ v kurze Planimetria a stereometria Tu.
V Euklidových Základoch sú uvedené prvé dve tvrdenia (symbolicky
T/I a
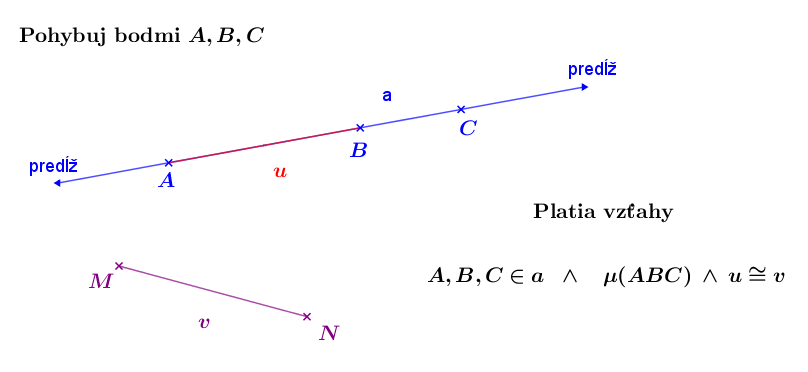
T/II), ktoré sa týkajúce existencie rovnostranného trojuholníka a "prenášania" úsečky do polohy s daným počiatočným bodom. Euklides dokazuje tieto tvrdenia formou konštrukcie resp. návodov ako postupovať pri dokazovaní týchto tvrdení.
V dôkaze T/II sa používa niečo ako pohyb, ale v skutočnosti sa tam nič nepohybuje.
V dôkaze T/II sa používa niečo ako pohyb, ale v skutočnosti sa tam nič nepohybuje.
Tvrdenia
- T/I: Vytvoriť rovnostranný trojuholník na danej konečnej priamke. Celé tvrdenie resp. celú konštrukciu nájdete Tu.
-
T/II: Z daného bodu
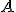 narysovať úsečku
narysovať úsečku 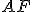 zhodnú s danou úsečkou
zhodnú s danou úsečkou 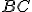 .
.
Dôkaz tvrdenia T/II prezentujeme vo forme dynamickej konštrukcie - appletu v programe GeoGebra.
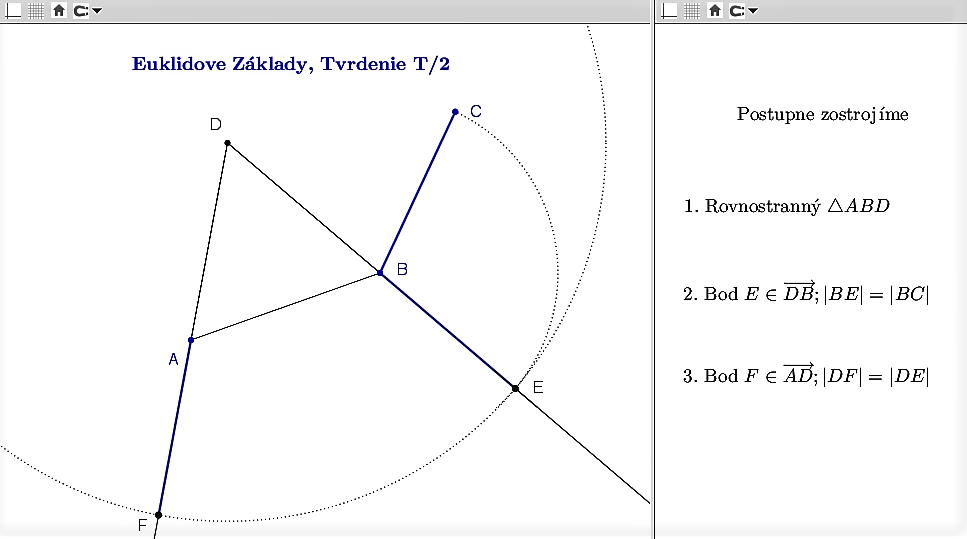
Applet si otvoríte programom GeoGebra Tu.
Applet si otvoríte programom GeoGebra Tu.
Poznámky
- Pri dokazovaní týchto prvých dvoch tvrdení Euklides využíva prvý postulát o existencii priamky určenej dvoma bodmi.
- Z hľadiska konštruovateľnosti tento postulát predstavuje existenciu pravítka.
- Zároveň využíva tretí postulát o možnosti zostrojenia kruhu určeného stredom a polomerom.
- Z hľadiska konštruovateľnosti to môžeme považovať za existenciu kružidla.
Definícia kruhu intuitívne používa pojmy "medzi" a "zhodnosť", ktoré nie sú v Základoch zavedené. Neskôr (takmer o dve tisíc rokov) tieto pojmy zavádza Hilbert vo svojom axiomatickom systéme, kde sa kružnica po uvedení axióm zhodnosti už môže zadefinovať.
Euklides v dôkazoch predpokladá, že pri prenášaní úsečky sa jej veľkosť nezmení. Toto v Hilbertovej sústave zabezpečujú axiómy zhodnosti.
Euklides v dôkazoch predpokladá, že pri prenášaní úsečky sa jej veľkosť nezmení. Toto v Hilbertovej sústave zabezpečujú axiómy zhodnosti.
Euklidovská konštrukcia sa nazýva grafická konštrukcia v euklidovskom priestore realizovaná
- ideálnym pravítkom a ideálnym kružidlom
- konečným počtom krokov
- každý krok je elementárna konštrukcia na zostrojenie
- priamky prechádzajúcej dvoma danými rôznymi bodmi
- kružnice so stredom v danom bode a s daným polomerom
- priesečníka dvoch rôznobežných priamok (resp. prieniku priamky a kružnice alebo prieniku dvoch kružníc).
Elementárne euklidovské konštrukcie
- Zostrojenie stredu danej úsečky.
- Zostrojenie osi úsečky, osi daného uhla.
- "Prenesenie" danej úsečky na danú polpriamku. Tvrdenie T/III.
- "Prenesenie" daného uhla na danú polpriamku v danej polrovine.
Poznámky
- V euklidovskej rovine prvé dve uvedené elementárne konštrukcie nie problém zrealizovať, ak máme k dispozícii pravítko a kružidlo. Pozrite si konštrukciu Tu.
- V geometrii, v ktorej neplatí piaty Euklidov postulát (neeuklidovské geometrie) to také jednoduché nebude. V prvom rade musíme nájsť odpoveď na otázku: "Čo budeme rozumieť pod pravítkom resp. kružidlom v takejto geometrii?"
- V ďalšej časti sa pokúsime zodpovedať na túto otázku a následne vytvoriť elementárne euklidovské konštrukcie v neeuklidovskej geometrii.
Definícia - rovnobežnosti
Euklides: Rovnoběžky jsou přímky, které jsou v téže rovině a prodlouženy na obě strany do nekonečna nikde se nesbíhají. (Servít)
Hilbert: Dve priamky sú rovnobežné (rovnobežky), ak nemajú spoločný bod.
Euklides: Rovnoběžky jsou přímky, které jsou v téže rovině a prodlouženy na obě strany do nekonečna nikde se nesbíhají. (Servít)
Hilbert: Dve priamky sú rovnobežné (rovnobežky), ak nemajú spoločný bod.
Tvrdenie (Euklides, Základy, T/XXVII).
Keď priamka pretínajúca dve priamky vytvára striedavé uhly navzájom rovnaké, budú tie priamky navzájom rovnobežné.
Dôkaz
Cvičenie; dôsledok vety o vonkajšom uhle
Keď priamka pretínajúca dve priamky vytvára striedavé uhly navzájom rovnaké, budú tie priamky navzájom rovnobežné.
Dôkaz
Cvičenie; dôsledok vety o vonkajšom uhle
Dôsledok - existencia rovnobežky.
Nech bod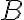 neleží na priamke
neleží na priamke
 . Potom existuje priamka
. Potom existuje priamka
 taká, že
taká, že
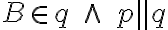 .
.
Dôkaz.
Zvoľme si ľubovoľný bod na priamke
na priamke
 . Zostrojme priamku
. Zostrojme priamku
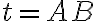 (transverzála/priečka priamok
(transverzála/priečka priamok
 ).
).
Následne zostrojíme priamku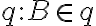 tak, aby striedavé uhly pri priamkach
tak, aby striedavé uhly pri priamkach
 s transverzálou
s transverzálou
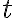 boli rovnaké (axióm Z4).
boli rovnaké (axióm Z4).
Rovnobežnosť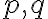 vyplýva z vety o vonkajšom uhle trojuholníka.
vyplýva z vety o vonkajšom uhle trojuholníka.
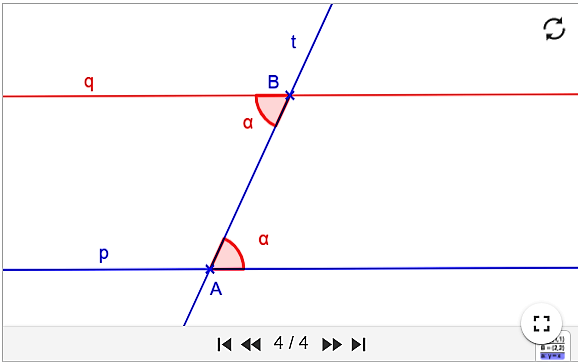
Applet aktivujete Tu
Nech bod
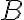 neleží na priamke
neleží na priamke
 . Potom existuje priamka
. Potom existuje priamka
 taká, že
taká, že
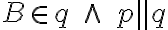 .
.
Dôkaz.
Zvoľme si ľubovoľný bod
 na priamke
na priamke
 . Zostrojme priamku
. Zostrojme priamku
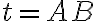 (transverzála/priečka priamok
(transverzála/priečka priamok
 ).
).
Následne zostrojíme priamku
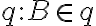 tak, aby striedavé uhly pri priamkach
tak, aby striedavé uhly pri priamkach
 s transverzálou
s transverzálou
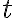 boli rovnaké (axióm Z4).
boli rovnaké (axióm Z4).
Rovnobežnosť
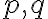 vyplýva z vety o vonkajšom uhle trojuholníka.
vyplýva z vety o vonkajšom uhle trojuholníka.

Applet aktivujete Tu
Poznámka.
Dokázaním predchádzajúceho dôsledku sme ukázali existenciu rovnobežky, pričom sme použili predchádzajúce axiómy.
Teraz stačí formulovať axiómu, ktorá zaručí jednoznačnosť - existenciu jedinej rovnobežky.
Dokázaním predchádzajúceho dôsledku sme ukázali existenciu rovnobežky, pričom sme použili predchádzajúce axiómy.
Teraz stačí formulovať axiómu, ktorá zaručí jednoznačnosť - existenciu jedinej rovnobežky.
Playfairova axióma.
Pre každú priamku a pre každý bod
a pre každý bod
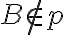 existuje práve (najviac) jedna priamka
existuje práve (najviac) jedna priamka
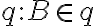 rovnobežná s priamkou
rovnobežná s priamkou
 (ozn.
(ozn.
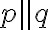 ).
).
Pre každú priamku
 a pre každý bod
a pre každý bod
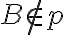 existuje práve (najviac) jedna priamka
existuje práve (najviac) jedna priamka
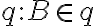 rovnobežná s priamkou
rovnobežná s priamkou
 (ozn.
(ozn.
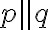 ).
).
Piaty Euklidov postulát.
A keď priamka pretínajúca priamky dve priamky tvorí na tej istej strane vnútornej (priľahlej) uhly menšie dvoch pravých, tie dve priamky predĺžené do nekonečna sa zbiehajú na tej strane, kde sú uhly menšie dvoch pravých.
A keď priamka pretínajúca priamky dve priamky tvorí na tej istej strane vnútornej (priľahlej) uhly menšie dvoch pravých, tie dve priamky predĺžené do nekonečna sa zbiehajú na tej strane, kde sú uhly menšie dvoch pravých.
Tvrdenie(Základy, T/XXXII).
Súčet vnútorných uhlov trojuholníka je rovný dvom pravým uhlom.
Dôkaz
Cvičenie; tvrdenie je ekvivalentné axióme rovnobežnosti.
Súčet vnútorných uhlov trojuholníka je rovný dvom pravým uhlom.
Dôkaz
Cvičenie; tvrdenie je ekvivalentné axióme rovnobežnosti.
Neeuklidovská geometria je taká geometria, v ktorej neplatí piaty Euklidov postulát - axióma rovnobežnosti ale spĺňa axiómy incidencie, usporiadania a zhodnosti.
Neeuklidovské geometrie rozdeľujeme do dvoch kategórií:
- Hyperbolická geometria, v ktorej daným bodom neležiacim na danej priamke prechádzajú aspoň dve rovnobežky.
- Parabolická geometria, v ktorej neexistuje žiadna rovnobežka idúca daným bodom neležiacim na danej priamke. My sa budeme zaoberať len hyperbolickou geometriou. Popíšeme dva modely, ktoré reprezentujú hyperbolickú rovinu.
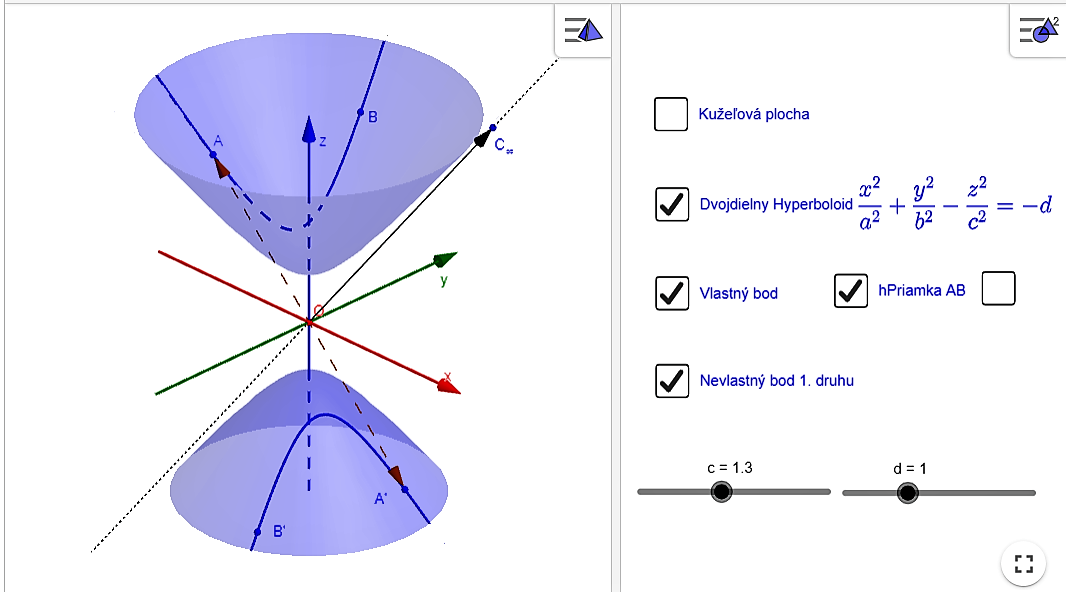
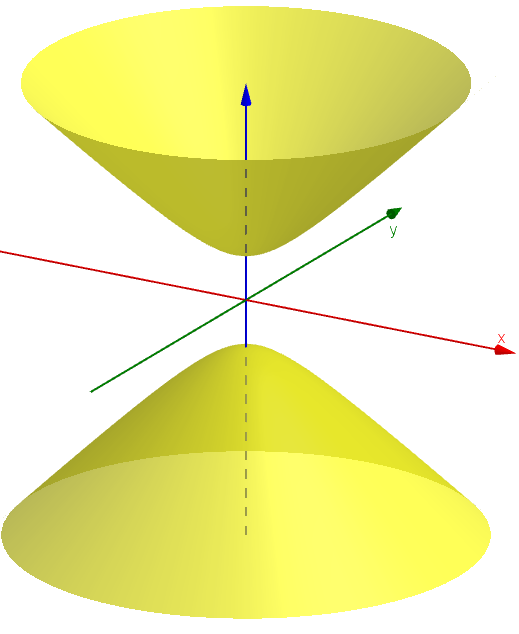
Za východisko pre hyperbolickú rovinu si vezmeme dvojdielny hyperboloid
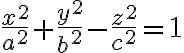 , na ktorom urobíme dve základné operácie.
, na ktorom urobíme dve základné operácie.
Applet si otvoríte programom GeoGebra Tu
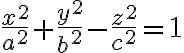 , na ktorom urobíme dve základné operácie.
, na ktorom urobíme dve základné operácie.
Applet si otvoríte programom GeoGebra Tu
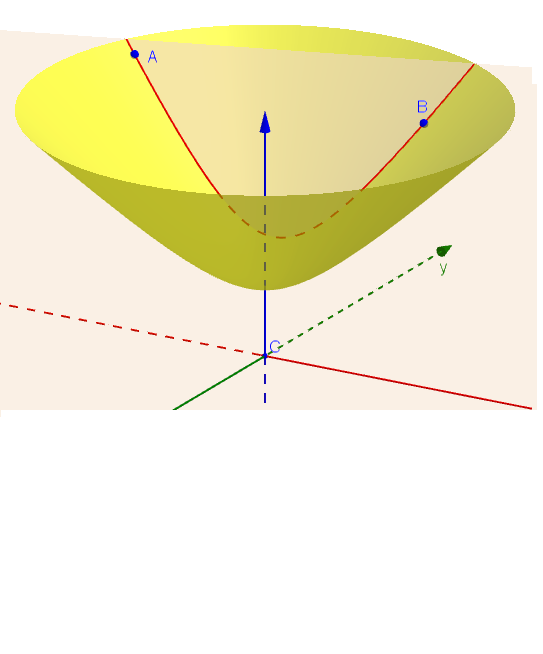
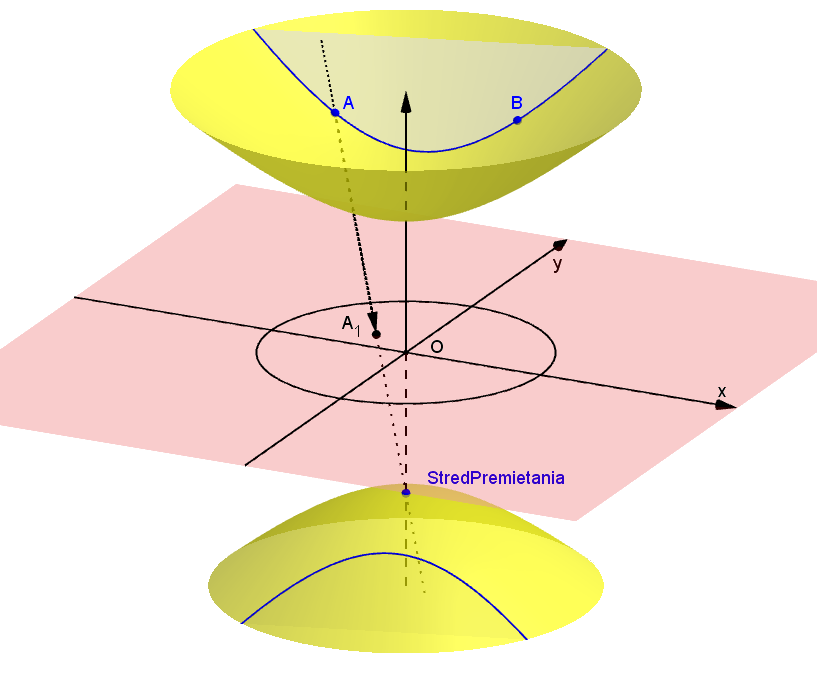
- Najprv vykonáme operáciu "stotožnenie" každých dvoch bodov hyperboloidu súmerných podľa jeho stredu. Takouto operáciou redukujeme daný hyperboloid len na jednu jeho časť. Takúto dvojicu bodov nazývame združené body. V ďalších úvahách budeme pracovať len s jeho jednou časťou hyperboloidu, napríklad s "hornou časťou", pozrite si pravý obrázok.
- Potom urobíme prienik (rez) hyperboloidu s ľubovoľnou stredovou rovinou. Takáto stredová rovina môže byť trojakého typu: reálne pretína hyperboloid v hyperbole, môže sa dotýkať hyperboloidu alebo ho nepretína v reálnom prieniku. Po uskutočnení týchto dvoch základných operácií môžeme definovať základné pojmy pre hyperbolickú rovinu.
- Bod hyperbolickej roviny: dvojicu
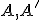 združených bodov hyperboloidu nazveme vlastný h-bod hyperbolickej roviny alebo len h-bod.
združených bodov hyperboloidu nazveme vlastný h-bod hyperbolickej roviny alebo len h-bod. - Priamka hyperbolickej roviny: ak prienikom stredovej roviny s hyperboloidom je hyperbola, tak túto krivku (hyperbolu) nazývame vlastná h-priamka alebo len krátko h-priamka.
- V nižšie uvedených poznámkach nájdete definície nevlastných bodov a priamok.
Poznámky.
- Stredová rovina (priamka) je rovina (priamka) prechádzajúca stredom
 hyperboloidu.
hyperboloidu. - Asymptotická kužeľová plocha je rotačná plocha, ktorá sa dotýka rotačného hyperboloidu v nevlastnej kužeľosečke.
- Nevlastný (limitný) bod
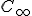 hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu.
hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu. - Nevlastné body priestoru Euklidovského priestoru, ktoré na ploche hyperboloidu neležia, nazývame nevlastný h-bod 2. druhu.
- Keďže rezy stredových rovín s hyperboloidom môžu byť trojakého typu, existujú tri typy hyperbolických h-priamok:
- ak prienik obsahuje len povrchovú priamku asymptotickej kužeľovej plochy (rovina sa dotýka hyperboloidu v nekonečne), tak tento prienik budeme považovať za nevlastnú h-priamku 1. druhu (rovina hyperboloid reálne pretne v komplexne združených rovnobežkách)
- ak stredová rovina nepretína hyperboloid, tak rezom je imaginárna kužeľosečka (elipsa), ktorú nazveme nevlastná h-priamka 2. druhu.
Poincaré model
- model vznikne ako stredový priemet dvojdielneho hyperboloidu
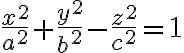
- stred premietanie je vrchol
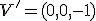 (spodná časť) hyperboloidu
(spodná časť) hyperboloidu - premietame do roviny kolmej na os hyperboloidu, ktorá prechádza stredom hyperboloidu
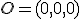
- priemetom hyperboloidu
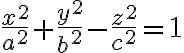 je zrejme otvorený kruh
je zrejme otvorený kruh 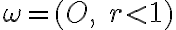
- tento otvorený kruh so stredom
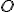 sa nazýva Poincaré Disc
sa nazýva Poincaré Disc - dvojdielny hyperboloid a rovina kolmá na os hyperboloidu prechádzajúca jeho stredom Tu.
Tvrdenie
Dôkaz
- Dôkaz prvej časti tohto tvrdenia vyplýva z vlastností stredového premietania, v ktorom sa kužeľová plocha obaľujúca hyperboloid zobrazí do kružnice
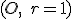 . To znamená, že ľubovoľný bod hyperboloidu sa zobrazí do vnútra kruhu
. To znamená, že ľubovoľný bod hyperboloidu sa zobrazí do vnútra kruhu 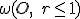 . Otvorte si obrázok Tu
. Otvorte si obrázok Tu - Dôkaz druhej časti o priemete h-priamky (reálne stredovej hyperboly) rozdelíme na dve etapy i. a ii.
Pohybujte bodmi , applet si stiahnete Tu.
, applet si stiahnete Tu.
- Nech
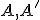 je dvojica združených bodov hyperboloidu a nech
je dvojica združených bodov hyperboloidu a nech 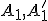 sú ich stredové priemety. Pre súčin vzdialeností
sú ich stredové priemety. Pre súčin vzdialeností
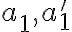 bodov
bodov 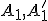 od stredu
od stredu  hyperboloidu platí:
hyperboloidu platí:
![a_1 \times a'_1=[ \frac{1}{r}(\sqrt{r^2+1}-1)] \times [\frac{1}{r}(\sqrt{r^2+1}+1)]=1 a_1 \times a'_1=[ \frac{1}{r}(\sqrt{r^2+1}-1)] \times [\frac{1}{r}(\sqrt{r^2+1}+1)]=1](https://lms.umb.sk/filter/tex/pix.php/bd6f2c6a62689c2e552273cc589b6f51.png) .
.
Dôkaz toho, že súčin vzdialeností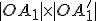 je konštantný je prezentovaný v nižšie priloženom applete. Pozrite si obrázok a otvorte si applet.
je konštantný je prezentovaný v nižšie priloženom applete. Pozrite si obrázok a otvorte si applet.
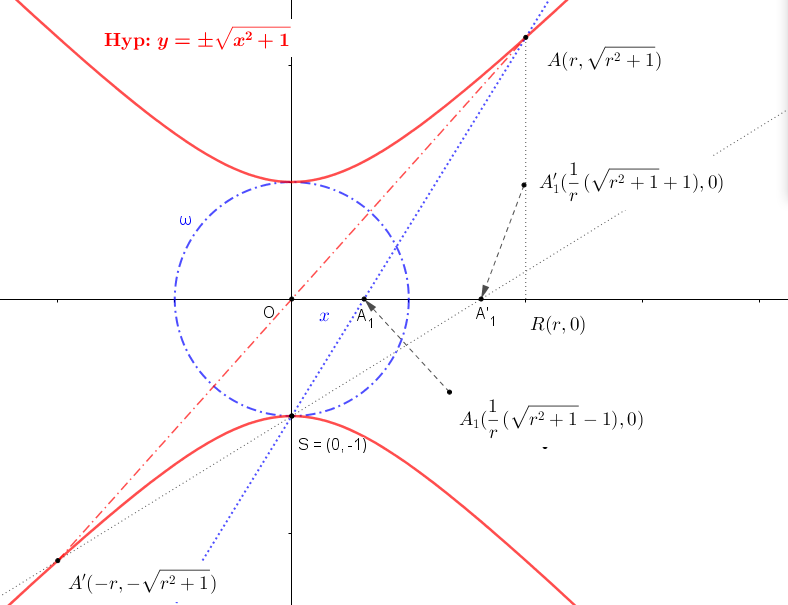
Obrázok, applet si otvoríte programom GeoGebra Tu. - Musíme ešte dokázať, že ľubovoľná dvojica združených bodov
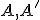 leží na kružnici kolmej na kružnicu
leží na kružnici kolmej na kružnicu 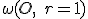 . V tejto etape dôkazu budeme potrebovať tvrdenie o mocnosti bodu ku kružnici. Viac o mocnosti bodu ku kružnice nájdete v kurze Planimetria a stereometria
Tu.
. V tejto etape dôkazu budeme potrebovať tvrdenie o mocnosti bodu ku kružnici. Viac o mocnosti bodu ku kružnice nájdete v kurze Planimetria a stereometria
Tu.
- Nech
Mocnosť bodu ku kružnici
Je daná kružnica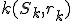 a bod
a bod  , ležiaci zvonka kružnice. Nech
, ležiaci zvonka kružnice. Nech  je sečnica kružnice
je sečnica kružnice  vedená bodom
vedená bodom  a
nech
a
nech 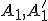 sú priesečníky sečnice
sú priesečníky sečnice  s kružnicou
s kružnicou 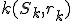 .
Pod mocnosťou bodu
.
Pod mocnosťou bodu  ku kružnici
ku kružnici 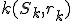 rozumieme číslo
rozumieme číslo 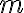 , pre ktoré platí:
, pre ktoré platí: 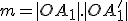 .
.
Je daná kružnica
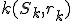 a bod
a bod  , ležiaci zvonka kružnice. Nech
, ležiaci zvonka kružnice. Nech  je sečnica kružnice
je sečnica kružnice  vedená bodom
vedená bodom  a
nech
a
nech 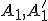 sú priesečníky sečnice
sú priesečníky sečnice  s kružnicou
s kružnicou 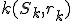 .
Pod mocnosťou bodu
.
Pod mocnosťou bodu  ku kružnici
ku kružnici 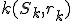 rozumieme číslo
rozumieme číslo 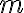 , pre ktoré platí:
, pre ktoré platí: 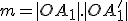 .
.
Vlastnosť mocnosť stačí vhodne aplikovať na náš prípad. Ilustráciu tvrdenia o priemete h-priamky prezentuje nasledujúci applete. Podrobný dôkaz (časti ii.) nájde čitateľ v ďalšej podkapitole s názvom "Hyperbolická priamka". Pozrite si tiež kapitolu "The Poincaré Disk Model" v práci [HIT].
Pokračovanie dôkazu tvrdenia o priemete h-priamky, v ktorom využijeme tvrdenie o mocnosti bodu ku kružnici.
Tvrdenie
Priemetom h-priamky (hyperboly) je otvorený kružnicový oblúk, ktorý je kolmý na hranicu kruhu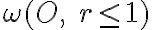 .
.
Pri dôkaze budeme potrebovať aj pojem dvojice inverzných bodov a pojem polárneho prvku v kruhovej inverzii. Viac o kruhovej inverzii najdete v kurze Planimetria a stereometria
Tu. Najskôr dokážeme lemu:
Priemetom h-priamky (hyperboly) je otvorený kružnicový oblúk, ktorý je kolmý na hranicu kruhu
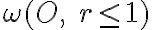 .
.
Lema
Nech je daná kruhová inverzia určená kružnicou - hranicou kruhu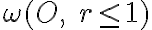 a nech bod
a nech bod 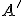 je obrazom bodu
je obrazom bodu 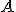 v tejto kruhovej inverzii. Zvoľme si kružnicu
v tejto kruhovej inverzii. Zvoľme si kružnicu  obsahujúcu dvojicu inverzných bodov
obsahujúcu dvojicu inverzných bodov 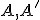 . Ak kružnica
. Ak kružnica  pozostáva výlučne z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu
pozostáva výlučne z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu 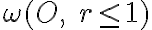 , tak kružnica
, tak kružnica  pretína kružnicu - hranicu kruhu
pretína kružnicu - hranicu kruhu 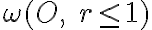 kolmo.
kolmo.
Nech je daná kruhová inverzia určená kružnicou - hranicou kruhu
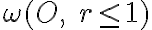 a nech bod
a nech bod 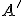 je obrazom bodu
je obrazom bodu 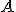 v tejto kruhovej inverzii. Zvoľme si kružnicu
v tejto kruhovej inverzii. Zvoľme si kružnicu  obsahujúcu dvojicu inverzných bodov
obsahujúcu dvojicu inverzných bodov 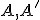 . Ak kružnica
. Ak kružnica  pozostáva výlučne z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu
pozostáva výlučne z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu 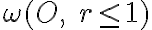 , tak kružnica
, tak kružnica  pretína kružnicu - hranicu kruhu
pretína kružnicu - hranicu kruhu 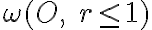 kolmo.
kolmo.
Dôkaz
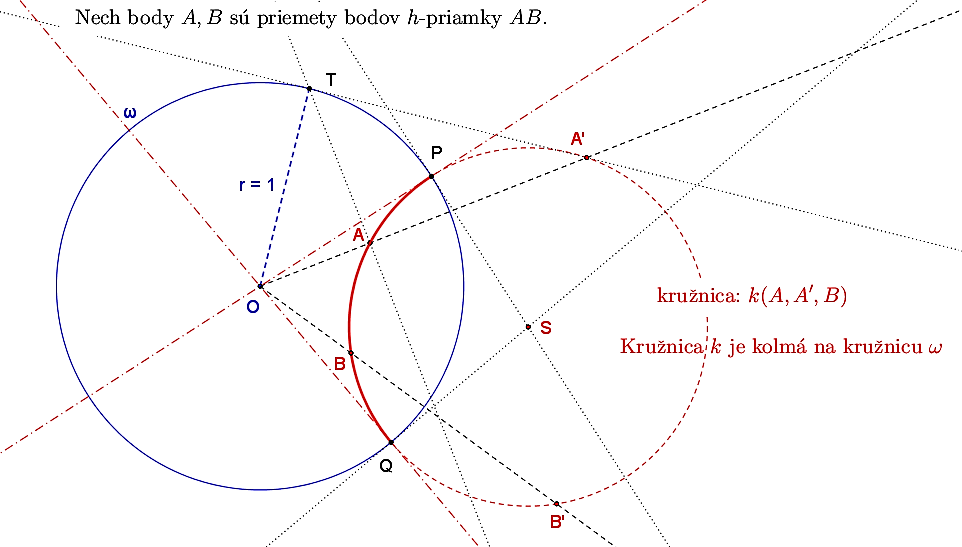
- Nech body
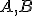 sú priemety bodov h-priamky
sú priemety bodov h-priamky 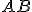 . Pozrite si priložený obrázok.
. Pozrite si priložený obrázok. - Podľa predchádzajúcej časti dôkazu (i.) platí
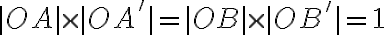 .
. - Odkiaľ: bod
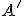 je obrazom bodu
je obrazom bodu 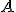 aj v kruhovej inverzii
aj v kruhovej inverzii 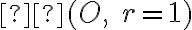 . Podobne to môžeme povedať aj o bodoch
. Podobne to môžeme povedať aj o bodoch 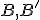 .
. - Nech
 je kružnica určená bodmi
je kružnica určená bodmi 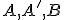 , potom v dôsledku mocnosti bodu
, potom v dôsledku mocnosti bodu 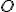 ku kružnici
ku kružnici  bude aj bod
bude aj bod 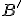 bodom kružnice
bodom kružnice  .
. - Teraz uvažujme o dotykových bodoch
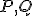 na dotyčniciach z bodu
na dotyčniciach z bodu 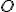 ku kružnici
ku kružnici  .
. - Mocnosť bodov
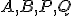 ku kružnici
ku kružnici 
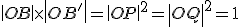
- Z toho vyplýva, že body
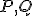 sú samodružné v kruhovej inverzii
sú samodružné v kruhovej inverzii 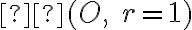 .
. - Priamky
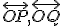 sú dotyčnice ku kružnici
sú dotyčnice ku kružnici  . Odkiaľ
. Odkiaľ 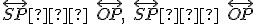 .
. - Kružnica
 je kolmá na kružnicu
je kolmá na kružnicu 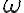 .
Tým je dôkaz lemy ukončený.
.
Tým je dôkaz lemy ukončený.
Otvorte si applet v programe GeoGebra - dôkaz Tu. Pozrite si tiež prácu [HYP].

V dôsledku lemy a predchádzajúcich častí dôkazu môžeme vysloviť tvrdenie:
Priemetom h-priamky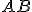 je oblúk
je oblúk 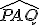 na kružnici
na kružnici  .
.
Priemetom h-priamky
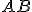 je oblúk
je oblúk 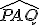 na kružnici
na kružnici  .
.
Poincaré diskový model (tiež sa používa označenie Poincaré Disc) hyperbolickej roviny je prezentovaný v euklidovskej rovine ako otvorený kruh
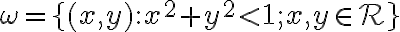 . Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
. Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
V predchádzajúcej časti sme uviedli, že tento otvorený kruh je stredovým priemetom dvojdielneho hyperboloidu. Uviedli sme tvrdenie, že v Poincaré diskovom modeli pre hyperbolické body a hyperbolické priamky platí:
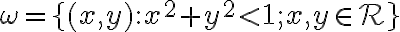 . Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
. Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
V predchádzajúcej časti sme uviedli, že tento otvorený kruh je stredovým priemetom dvojdielneho hyperboloidu. Uviedli sme tvrdenie, že v Poincaré diskovom modeli pre hyperbolické body a hyperbolické priamky platí:
- vlastný bod je vnútorný bod kruhu, ktorý je priemetom vlastného h-bodu hyperboloidu;
- koncový bod (resp. nevlastný bod) ležiaci na hranici kruhu, ktorý je priemetom nevlastného bodu 1. druhu;
- priamka je otvorený kružnicový oblúk kruhu - je priemetom h-priamky (hyperboly), pričom tento oblúk leží na kružnici kolmej na hranicu kruhu
Pri zostrojovaní hyperbolickej priamky určenej dvoma bodmi kruhu s výhodou využijeme vlastnosti kruhovej inverzie a konštrukcie popísané v predchádzajúcom dôkaze.
Poznámky
- V ďalšej podkapitole navrhneme v prostredí GeoGebra konštrukciu a zároveň aj nástroj na zostrojenie hyperbolickej priamky určenej dvoma rôznymi bodmi v Poincaré modeli disku. V konštrukcii využijeme inverzné body.
- Pri riešení konštrukčných úloh v Poincaré modeli potrebujeme okrem konštrukcie hyperbolickej priamky (nasledujúca kapitola) potrebovať aj konštrukciu kružnice a ďalších základných euklidovských konštrukcií (kolmica, os úsečky a pod).
Poznámky.
- Konštrukcie v Poincare Disc si uľahčíme, ak v GeoGebre vytvoríme vlastné nástroje, ktorými sa "vykreslí" resp. zostrojí požadovaný útvar.
- Vychádzame z tvrdenia, že h-priamka sa zobrazí do kružnicového oblúku, ktorý leží na kružnici kolmej k Poincare disku.
- Najskôr musíme popísať konštrukciu, ktorá vytvorí požadovaný kolmý oblúk (obraz h-priamky).
- Potom pomocou makier vytvoríme nástroj, pomocou ktorého sa zostrojí požadovaný kolmý oblúk.
Úloha.
Daný je kruh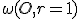 a body
a body 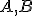 ležiace vnútri kruhu. Zostrojte obraz hyperbolickej h-
priamky určenej bodmi
ležiace vnútri kruhu. Zostrojte obraz hyperbolickej h-
priamky určenej bodmi 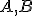 v prostredí GeoGebry
v prostredí GeoGebry
Daný je kruh
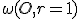 a body
a body 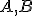 ležiace vnútri kruhu. Zostrojte obraz hyperbolickej h-
priamky určenej bodmi
ležiace vnútri kruhu. Zostrojte obraz hyperbolickej h-
priamky určenej bodmi 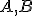 v prostredí GeoGebry
v prostredí GeoGebry
Riešenie
Budeme predpokladať, že aspoň jeden z bodov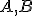 je vnútorný bod kruhu
je vnútorný bod kruhu 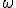 a je rôzny od stredu
a je rôzny od stredu 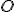 .
.
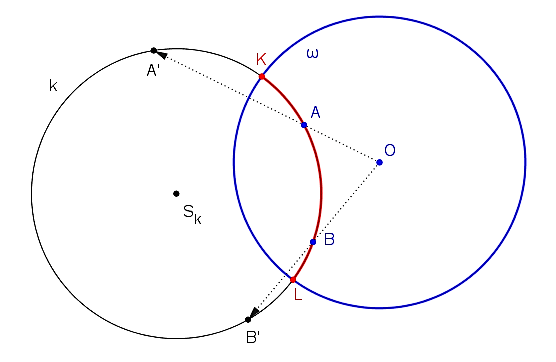
Postup konštrukcie
Budeme predpokladať, že aspoň jeden z bodov
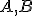 je vnútorný bod kruhu
je vnútorný bod kruhu 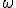 a je rôzny od stredu
a je rôzny od stredu 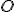 .
.

Postup konštrukcie
- V kruhovej inverzii
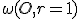 zostrojíme obrazy
zostrojíme obrazy 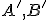 bodov
bodov 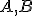 .
. - Zostrojíme kružnicu
 určenú bodmi
určenú bodmi 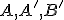 alebo bodmi
alebo bodmi 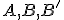 . Nájdeme priesečníky
. Nájdeme priesečníky 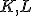 .
. - Na kružnici
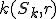 vyznačíme menší z oblúkov, ktoré sú určené krajnými bodmi
vyznačíme menší z oblúkov, ktoré sú určené krajnými bodmi 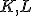 .
. - Menší oblúk je hľadaný obraz hyperbolickej priamky
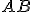
Nástroj na vytvorenie h-priamky v modeli Poincaré Disc.
- Nástroj v GeoGebre na zostrojenie priamky v modeli Poincaré Disc
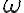 s polomerom
s polomerom 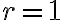 , otvorte
Tu. Postup je klasický ako v euklidovskej rovine. Najskôr si zvoľte dva rôzne body vo vnútri kruhu
, otvorte
Tu. Postup je klasický ako v euklidovskej rovine. Najskôr si zvoľte dva rôzne body vo vnútri kruhu 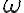 - použite nástroja Bod. Potom aktivujte nástroj hPriamka a program vykreslí kružnicový oblúk, ktorý je priemetom h-priamky (hyperboly). alebo
- použite nástroja Bod. Potom aktivujte nástroj hPriamka a program vykreslí kružnicový oblúk, ktorý je priemetom h-priamky (hyperboly). alebo
-
Nástroj v GeoGebre na zostrojenie priamky v modeli Poincaré Disc s ľubovoľným polomerom, otvorte
Tu. Pri tomto nástroji treba po zadaní dvoch bodov a aktivovaní nástroja hPriamka ešte kliknúť aj bod
 . Pomocou tohto bodu môžeme meniť polomer kružnice
. Pomocou tohto bodu môžeme meniť polomer kružnice 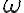 , čo predstavuje "sploštenie" hyperboloidu.
, čo predstavuje "sploštenie" hyperboloidu.
Postup na vytvorenie nástroja hPriamka v GeoGebre, pomocou ktorého sa narysuje obraz hyperbolickej priamky v Poincare modeli.
- Spustite program GeoGebra a otvorte si súbor uložený s názvom "h-Priamka".
- V základnom Menu programu GeoGebra vyberte možnosť "Vytvoriť nový nástroj".
- Postupujte podľa pokynov pre vytvorenie nástroja:
- ako výstupné objekty vyberte body:
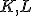 a oblúk
a oblúk  (otvorte si aj algebraické okno)
(otvorte si aj algebraické okno) - ako vstupné objekty vyberte body:
 a kružnicu
a kružnicu 
- vhodne pomenujte nástroj, napr. "hPriamka", vyberte predtým vytvorený obrázok pre ikonu
- v nápovedi uveďte napr. "Ukáž dva body a potom klikni na kružnicu"
- zaškrtnite políčko "Ukázať na palete nástrojov"
- uložte ako napr. "hPriamka" s príponou ggt.
- ako výstupné objekty vyberte body:
- Ak už vidíte novú ikonku nástroja hPriamka, tak v tejto konštrukcii kliknite v stĺpci Súbor na Nový.
- Nákresňa je "čistá" ale ikonka hPriamka je tam. Teraz si vytvorte kružnicu
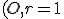 a vhodne zväčšite plochu nárysne. Uložtesi tento súbor
pod názvom Nástroj hPriamka.
a vhodne zväčšite plochu nárysne. Uložtesi tento súbor
pod názvom Nástroj hPriamka.
Cvičenie.
Vytvorte Nástroj/Ikonu v GeoGebre, pomocou ktorej sa vytvorí hyperbolická úsečka v modeli Poincaré Disk. Riešenie Tu
Vytvorte Nástroj/Ikonu v GeoGebre, pomocou ktorej sa vytvorí hyperbolická úsečka v modeli Poincaré Disk. Riešenie Tu
Nech sú dané dva rôzne body  a
a  na hyperboloide. Pozrite si nižšie priložený applet.
na hyperboloide. Pozrite si nižšie priložený applet.
 a
a  na hyperboloide. Pozrite si nižšie priložený applet.
na hyperboloide. Pozrite si nižšie priložený applet.- Uvažujme o kružnici
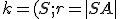 , ktorej všetky body sú bodmi hyperboloidu. Symbolicky:
, ktorej všetky body sú bodmi hyperboloidu. Symbolicky: 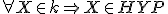 .
. - Nech bod
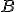 je stredovo súmerný k bodu
je stredovo súmerný k bodu  podľa stredu
podľa stredu  , potom bod
, potom bod 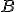 je tiež bodom kružnice
je tiež bodom kružnice  a zároveň bodom hyperboloidu.
a zároveň bodom hyperboloidu. - Nech
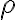 je určená bodmi
je určená bodmi 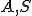 a bodom StredPremietania. Táto rovina pretína daný dvojdielny hyperboloid v hyperbole (v applete červená krivka).
a bodom StredPremietania. Táto rovina pretína daný dvojdielny hyperboloid v hyperbole (v applete červená krivka). - Zostrojme dotyčnice k tejto hyperbole v bodoch
 a ich priesečník
a ich priesečník 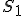 .
. - Potom platí nasledujúce tvrdenie, ktoré uvádzame bez dôkazu. K dôkazu sú potrebné širšie znalosti stredového premietania kužeľosečiek.
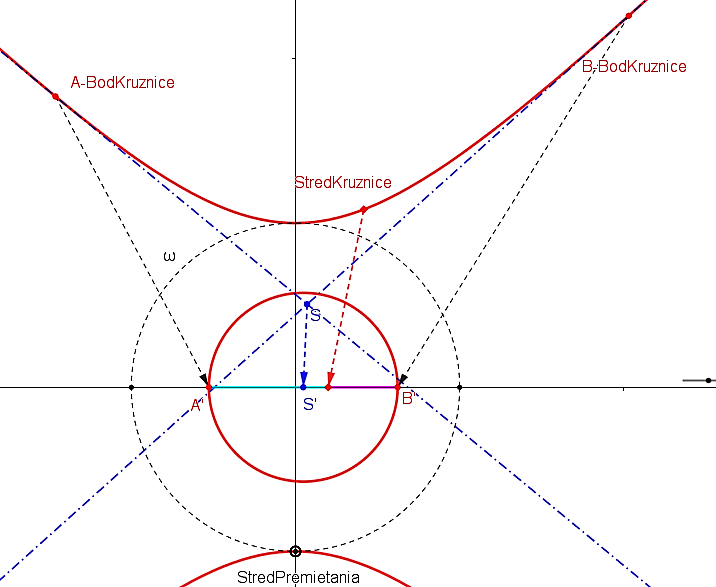
Otvorte si dynamický obrázok Tu.
Poznámka.
Na základe tohto tvrdenia môžeme uskutočniť konštrukciu, pomocou ktorej zostrojíme kružnicu v Poincaré disku určenú stredom a bodom
a bodom  a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
Na základe tohto tvrdenia môžeme uskutočniť konštrukciu, pomocou ktorej zostrojíme kružnicu v Poincaré disku určenú stredom
 a bodom
a bodom  a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
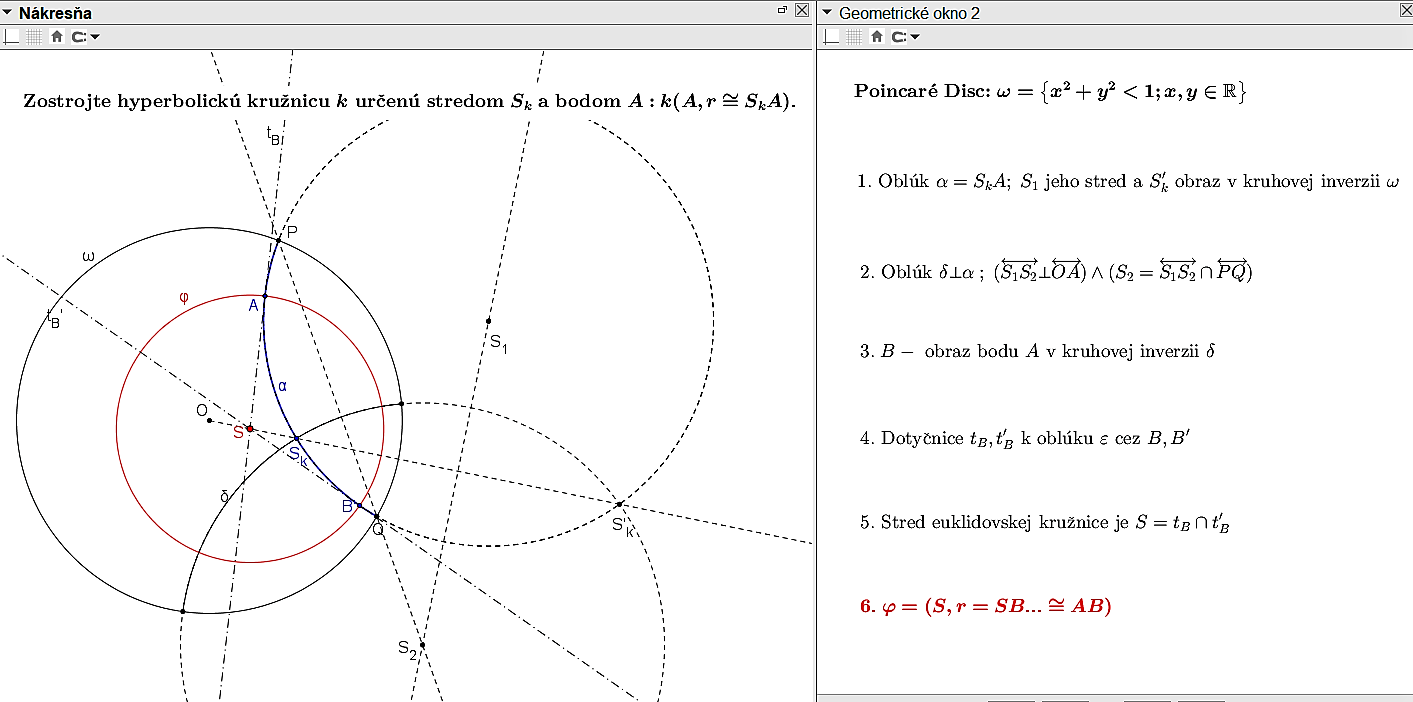
Otvorte si applet Tu
Poznámka.
Teraz už máme tri základné (euklidovské) nástroje: hPriamku hUsecku a hKružnicu v Geogebre. Otvorte si applet Tu.
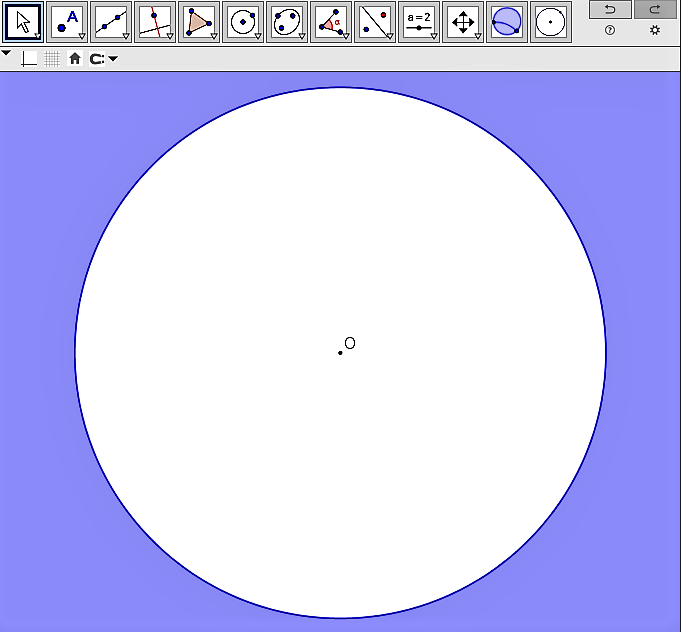
Teraz už máme tri základné (euklidovské) nástroje: hPriamku hUsecku a hKružnicu v Geogebre. Otvorte si applet Tu.

Beltramiho-Kleinov model
Model vznikne ako stredový priemet dvojdielneho hyperboloidu do roviny kolmej na os hyperboloidu, pričom
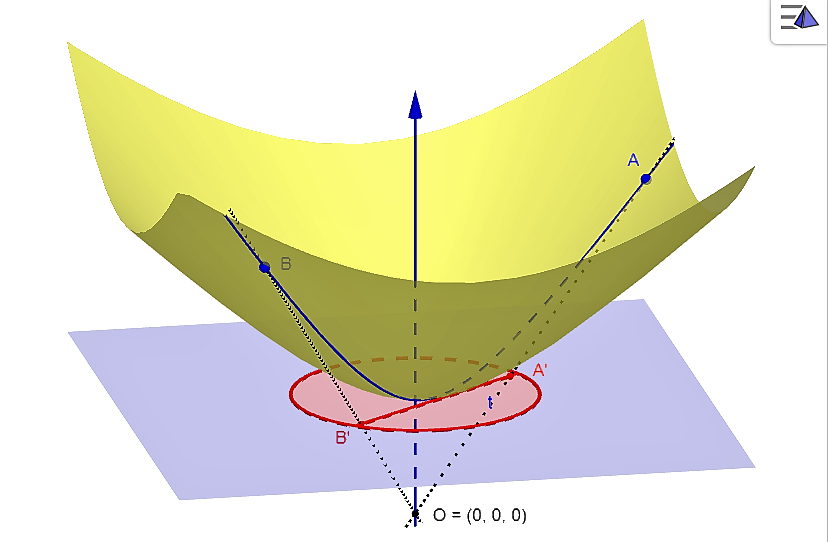
Model vznikne ako stredový priemet dvojdielneho hyperboloidu do roviny kolmej na os hyperboloidu, pričom
- stred premietanie je stred hyperboloidu - bod
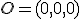
- rovina, do ktorej premietame je dotyková rovina hyperboloidu v jeho vrchole
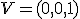
- priemetom hyperboloidu
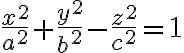 je otvorený kruh
je otvorený kruh 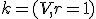 , ak
, ak 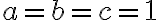
- zdôvodnite prečo priemetom hyperboloidu je práve otvorený kruh
- kruh s vrcholom
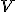 a polomerom
a polomerom 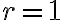 sa nazýva Klein Disc
sa nazýva Klein Disc - priemetom h-bodu (vlastného) hyperboloidu je zrejme vnútorný bod kruhu
- priemetom nevlastného h-bodu 1. druhu je hraničný bod tohto kruhu
- priemetom nevlastného h-bodu 2. druhu je vonkajší bod tohto kruhu
Zhrnutie
- Bodmi Beltrami Kleinovho modelu sú body Klein Disku.
- Priamkami sú tetivy tohto disku. Applet si aktivujete Tu.

V obidvoch hyperbolických modeloch (Beltrami a Poincare) neplatí axióma rovnobežnosti.
- V obidvoch prípadoch existuje viac ako jedna rovnobežka.
- Existencia rovnobežky vyplýva z prvých skupín axióm, ale jednoznačnosť nie.
- V modeli "Sféra" nemáme zaručenú ani existenciu rovnobežky.
- Kleinov disk a Poincaré disk sú modely, ktoré vzniknú aj premietaním pologule do vhodnej roviny/disku.
- Beltrami-Kleinov diskový model je ortografická projekcia (kolmé premietanie), zatiaľ čo Poincaré diskový model je stereografická projekcia (stredové premietanie). Pozri Wiki. alebo Disk a hyperboloid.
- Výhodou modelu Klein je, že priamky v tomto modeli sú euklidovské (rovné) tetivy. Nevýhodou je, že model nie je konformný (kruhy a uhly sú skreslené).
- Neeuklidovská hyperbolická geometria reprezentovaná Poincare diskom je konformná.
Cvičenia.
- Zostrojte rovnostranný trojuholník
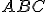 pomocou hyperbolických kružníc
pomocou hyperbolických kružníc 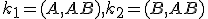 (pozrite si Euklidovo tvrdenie T/I).
(pozrite si Euklidovo tvrdenie T/I).
Riešenie Tu. - Zostrojte rovnoramenný trojuholník
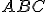 so základňou
so základňou 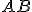 pomocou dvoch zhodných hyperbolických kružníc (kružnice s rovnakým polomerom).
Pomocou dotyčníc k hPriamkam
pomocou dvoch zhodných hyperbolických kružníc (kružnice s rovnakým polomerom).
Pomocou dotyčníc k hPriamkam 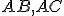 a k hPriamkam
a k hPriamkam 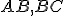 určte veľkosti uhlov pri základni a presvedčte sa, že majú rovnakú veľkosť. Riešenie Tu.
určte veľkosti uhlov pri základni a presvedčte sa, že majú rovnakú veľkosť. Riešenie Tu. - Zostrojte hyperbolickú priamku
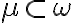 , ktorá je osou úsečky
, ktorá je osou úsečky 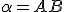 , kde
, kde 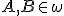 .
.
Návod:- Využitím Euklidovho tvrdenia T/I zostrojte hyperbolické rovnostranné trojuholník
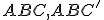 , kde
, kde 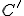 je súmerný bod podľa priamky
je súmerný bod podľa priamky 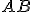 .
. - V trojuholníku
 zostrojte os prechádzajúcu vrcholmi
zostrojte os prechádzajúcu vrcholmi 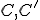 .
. - Využite Euklidove tvrdenia T/IX a T/X.
- Riešenie Tu.
- Využitím Euklidovho tvrdenia T/I zostrojte hyperbolické rovnostranné trojuholník
- Nájdite stred kružnice(pozrite si Euklidovo tvrdenie: Kniha III, T/I). Riešenie Tu.
- Zostrojte hyperbolickú kolmicu
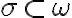 na hyperbolickú priamku
na hyperbolickú priamku 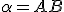 , ktorá prechádza bodom
, ktorá prechádza bodom 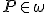 .
Pomocou dotyčníc k hPriamkam
.
Pomocou dotyčníc k hPriamkam 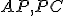 ukážte, že uhly pri päte kolmice sú pravé.
ukážte, že uhly pri päte kolmice sú pravé. - Zostrojte hyperbolickú kolmicu
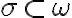 na hyperbolickú priamku
na hyperbolickú priamku 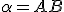 , ktorá prechádza bodom
, ktorá prechádza bodom 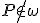 .
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
.
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
- Zostrojte kružnicu vpísanú (resp. opísanú) do trojuholníka
 (pozrite si Euklidovo tvrdenie: Kniha IV, T/IV (resp. T/V)).
(pozrite si Euklidovo tvrdenie: Kniha IV, T/IV (resp. T/V)).
Využite Poincaré Disc vytvorený v prostredí GeoGebra, v ktorom vieme zostrojiť hyperbolickú úsečku a priamku; kružnicu určenú stredom a bodom resp. polomerom; určiť vzdialenosť dvoch bodov.
Poincaré Disk si môžete stiahnuť Tu
Poincaré Disk si môžete stiahnuť Tu
Poznámky
- [CAS] Castellanos,J., NonEuclid: Interactive Javascript Software for Creating Straightedge and Collapsible Compass Constructions in the Disk Model of Hyperbolic Geometry. Dostupné Tu.
- [EUC] Euklidove Základy. Elektronická - verzia (angl.). Dostupné Tu.
- [GRE] Greenberg, M. (1993). Euclidean and non-Euclidean geometries. Third. Development and history. W. H. Freeman and Company, New York, 1993.
- [HIL] Hilbert, D., Grundlagen der Geometrie (Základy geometrie). 1899.
- [HIT] Hitchman, M. P., Geometry with an Introduction to Cosmic Topology. Oregon, USA 2018. Dostupné Tu.
- [HYP] Hyperbolic Geometry, Part III. Dostupné Tu.
- [CHAL] Chalmovianská, J., Axiomatika euklidovskej roviny. Dostupné Tu.
- [CHRI] M. Christersson, M., GeoGebra Constructions in the Disc. Dostupné Tu.
- [JOY] Joyce, D.E. Euclid's Elements, 1994. Dostupné Tu.
- [MAN] Manthey, J., GeoGebra Tools for Poincare Disk. Dostupné Tu.
- [SED] Šedivý, O., Vallo, D.: Základy elementárnej geometrie. FPV UKF v Nitre, 2009. ISBN : 978-80-8094-623-4.
- [SER] Servít, F., Eukleidovy Základy (Elementa). JČM, Praha, 1907. Dostupné Tu.
- Ukážka funkčného modelu "The hyperbolic plane" Tu, ktorý sme prevzali z https://www.geogebra.org/m/tHvDKWdC.
- [VAL] Vallo, D. (2021). Koncepcia výučby geometrie podporovanej implementáciou dynamických geometrických programov. Univerzita Konštantína Filozofa v Nitre. FPV Nitra, 2021.