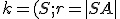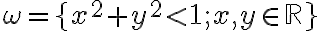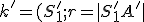Neeuklidovská geometria euklidovsky
Nech sú dané dva rôzne body  a
a  na hyperboloide. Pozrite si nižšie priložený applet.
na hyperboloide. Pozrite si nižšie priložený applet.
 a
a  na hyperboloide. Pozrite si nižšie priložený applet.
na hyperboloide. Pozrite si nižšie priložený applet.- Uvažujme o kružnici
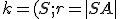 , ktorej všetky body sú bodmi hyperboloidu. Symbolicky:
, ktorej všetky body sú bodmi hyperboloidu. Symbolicky: 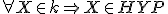 .
. - Nech bod
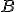 je stredovo súmerný k bodu
je stredovo súmerný k bodu  podľa stredu
podľa stredu  , potom bod
, potom bod 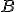 je tiež bodom kružnice
je tiež bodom kružnice  a zároveň bodom hyperboloidu.
a zároveň bodom hyperboloidu. - Nech
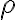 je určená bodmi
je určená bodmi 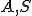 a bodom StredPremietania. Táto rovina pretína daný dvojdielny hyperboloid v hyperbole (v applete červená krivka).
a bodom StredPremietania. Táto rovina pretína daný dvojdielny hyperboloid v hyperbole (v applete červená krivka). - Zostrojme dotyčnice k tejto hyperbole v bodoch
 a ich priesečník
a ich priesečník 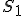 .
. - Potom platí nasledujúce tvrdenie, ktoré uvádzame bez dôkazu. K dôkazu sú potrebné širšie znalosti stredového premietania kužeľosečiek.
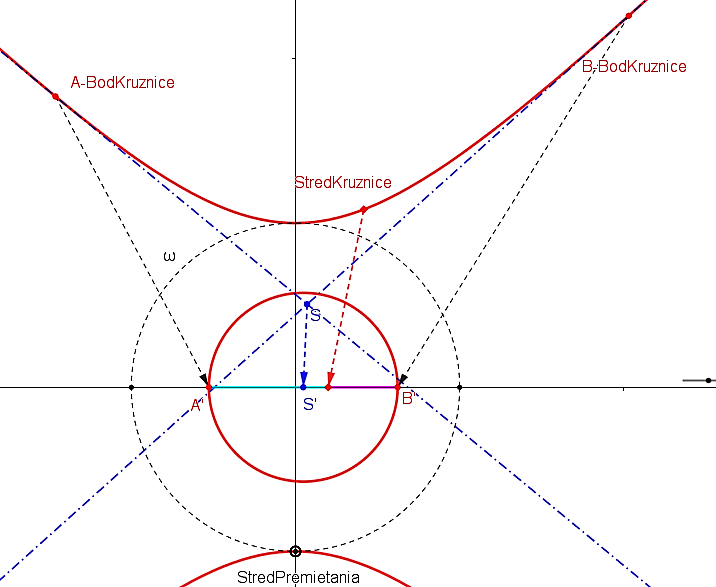
Otvorte si dynamický obrázok Tu.
Poznámka.
Na základe tohto tvrdenia môžeme uskutočniť konštrukciu, pomocou ktorej zostrojíme kružnicu v Poincaré disku určenú stredom a bodom
a bodom  a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
Na základe tohto tvrdenia môžeme uskutočniť konštrukciu, pomocou ktorej zostrojíme kružnicu v Poincaré disku určenú stredom
 a bodom
a bodom  a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
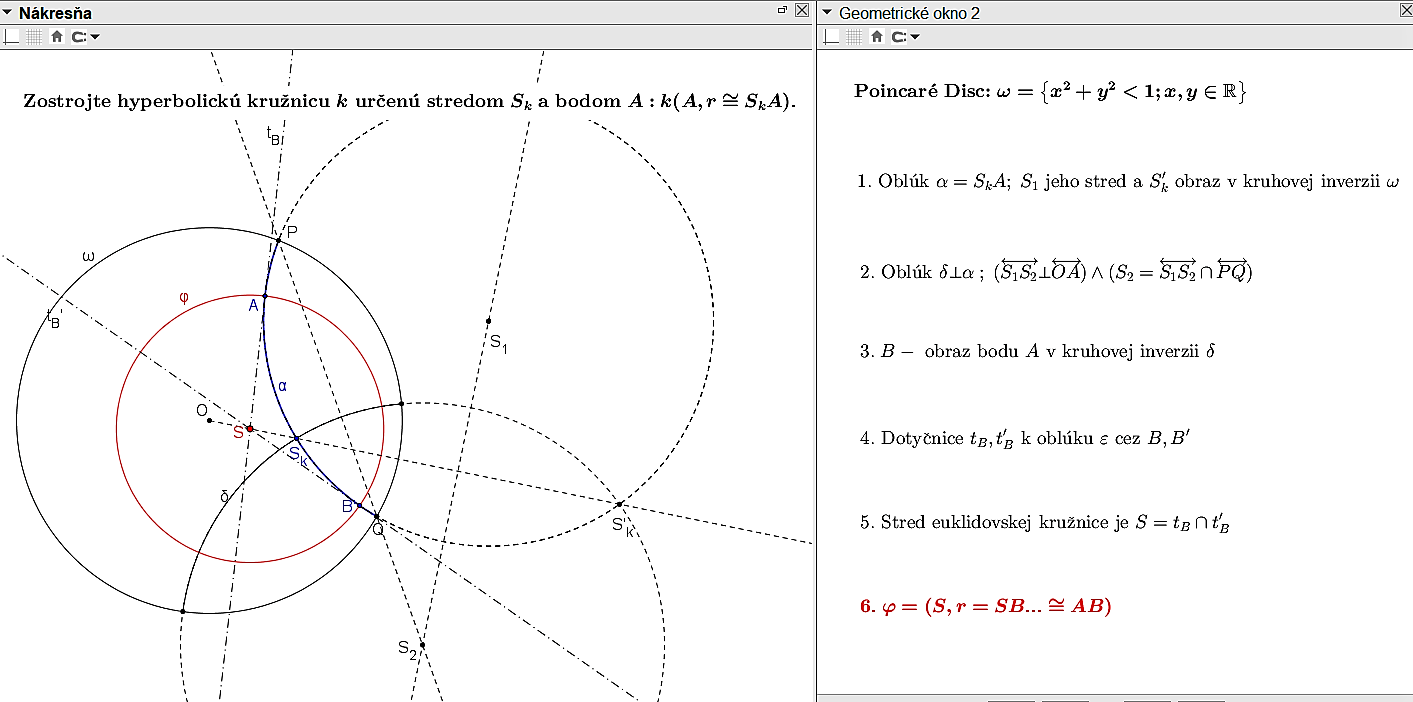
Otvorte si applet Tu
Poznámka.
Teraz už máme tri základné (euklidovské) nástroje: hPriamku hUsecku a hKružnicu v Geogebre. Otvorte si applet Tu.
Teraz už máme tri základné (euklidovské) nástroje: hPriamku hUsecku a hKružnicu v Geogebre. Otvorte si applet Tu.