Neeuklidovská geometria euklidovsky
Neeuklidovská geometria je taká geometria, v ktorej neplatí piaty Euklidov postulát - axióma rovnobežnosti ale spĺňa axiómy incidencie, usporiadania a zhodnosti.
Neeuklidovské geometrie rozdeľujeme do dvoch kategórií:
- Hyperbolická geometria, v ktorej daným bodom neležiacim na danej priamke prechádzajú aspoň dve rovnobežky.
- Parabolická geometria, v ktorej neexistuje žiadna rovnobežka idúca daným bodom neležiacim na danej priamke. My sa budeme zaoberať len hyperbolickou geometriou. Popíšeme dva modely, ktoré reprezentujú hyperbolickú rovinu.
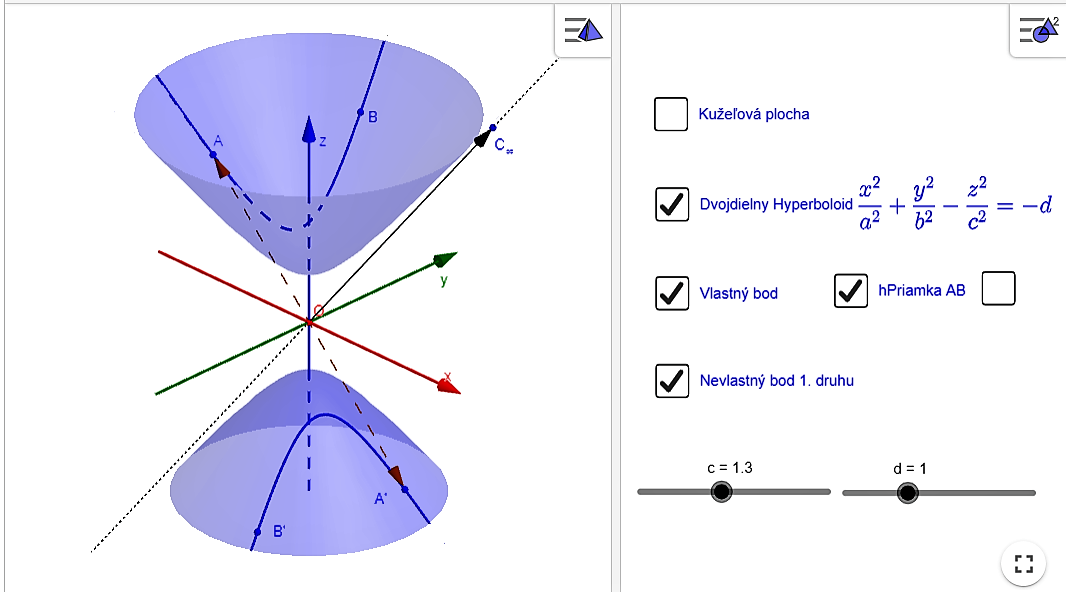
Za východisko pre hyperbolickú rovinu si vezmeme dvojdielny hyperboloid
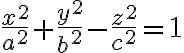 , na ktorom urobíme dve základné operácie.
, na ktorom urobíme dve základné operácie.
Applet si otvoríte programom GeoGebra Tu
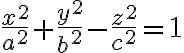 , na ktorom urobíme dve základné operácie.
, na ktorom urobíme dve základné operácie.
Applet si otvoríte programom GeoGebra Tu
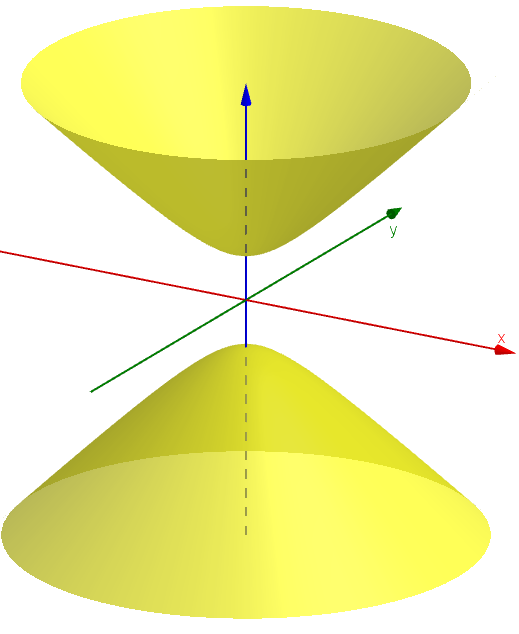
- Najprv vykonáme operáciu "stotožnenie" každých dvoch bodov hyperboloidu súmerných podľa jeho stredu. Takouto operáciou redukujeme daný hyperboloid len na jednu jeho časť. Takúto dvojicu bodov nazývame združené body. V ďalších úvahách budeme pracovať len s jeho jednou časťou hyperboloidu, napríklad s "hornou časťou", pozrite si pravý obrázok.
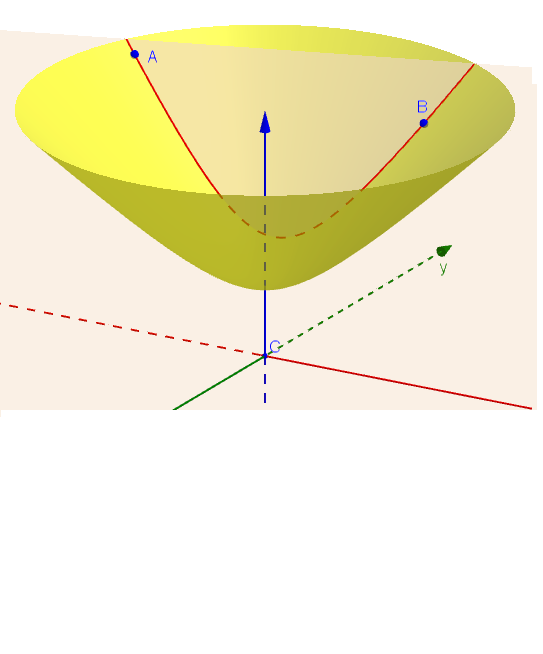
- Potom urobíme prienik (rez) hyperboloidu s ľubovoľnou stredovou rovinou. Takáto stredová rovina môže byť trojakého typu: reálne pretína hyperboloid v hyperbole, môže sa dotýkať hyperboloidu alebo ho nepretína v reálnom prieniku. Po uskutočnení týchto dvoch základných operácií môžeme definovať základné pojmy pre hyperbolickú rovinu.
- Bod hyperbolickej roviny: dvojicu
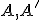 združených bodov hyperboloidu nazveme vlastný h-bod hyperbolickej roviny alebo len h-bod.
združených bodov hyperboloidu nazveme vlastný h-bod hyperbolickej roviny alebo len h-bod. - Priamka hyperbolickej roviny: ak prienikom stredovej roviny s hyperboloidom je hyperbola, tak túto krivku (hyperbolu) nazývame vlastná h-priamka alebo len krátko h-priamka.
- V nižšie uvedených poznámkach nájdete definície nevlastných bodov a priamok.
Poznámky.
- Stredová rovina (priamka) je rovina (priamka) prechádzajúca stredom
 hyperboloidu.
hyperboloidu. - Asymptotická kužeľová plocha je rotačná plocha, ktorá sa dotýka rotačného hyperboloidu v nevlastnej kužeľosečke.
- Nevlastný (limitný) bod
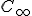 hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu.
hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu. - Nevlastné body priestoru Euklidovského priestoru, ktoré na ploche hyperboloidu neležia, nazývame nevlastný h-bod 2. druhu.
- Keďže rezy stredových rovín s hyperboloidom môžu byť trojakého typu, existujú tri typy hyperbolických h-priamok:
- ak prienik obsahuje len povrchovú priamku asymptotickej kužeľovej plochy (rovina sa dotýka hyperboloidu v nekonečne), tak tento prienik budeme považovať za nevlastnú h-priamku 1. druhu (rovina hyperboloid reálne pretne v komplexne združených rovnobežkách)
- ak stredová rovina nepretína hyperboloid, tak rezom je imaginárna kužeľosečka (elipsa), ktorú nazveme nevlastná h-priamka 2. druhu.