Kupcová, Ľ.: Nerovnosti a nerovnice
Úvod
Známe nerovnosti
Nech 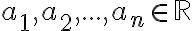 sú ľubovoľné reálne čísla. Potom platia nerovnosti:
sú ľubovoľné reálne čísla. Potom platia nerovnosti:
Harmonický priemer
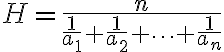
Geometrický priemer
![G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n} G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n}](https://lms.umb.sk/filter/tex/pix.php/a0b7c9933d767be06644db47123ab630.png)
Aritmetický priemer
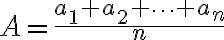
Kvadratický priemer
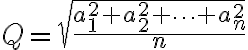
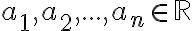 sú ľubovoľné reálne čísla. Potom platia nerovnosti:
sú ľubovoľné reálne čísla. Potom platia nerovnosti:
Harmonický priemer
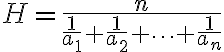
Geometrický priemer
![G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n} G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n}](https://lms.umb.sk/filter/tex/pix.php/a0b7c9933d767be06644db47123ab630.png)
Aritmetický priemer
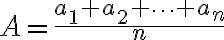
Kvadratický priemer
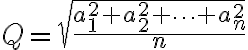
Dôkaz matematickou indukciou:
- Pre
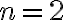 dôkaz je prijateľný na úrovni 1. ročníka strednej škola. Použijeme najskôr algebraické úpravy, pričom nerovnosť aritmetického a geometrického priemeru
dôkaz je prijateľný na úrovni 1. ročníka strednej škola. Použijeme najskôr algebraické úpravy, pričom nerovnosť aritmetického a geometrického priemeru
![\frac{a+b}{2} \geq \sqrt[]{ab} \frac{a+b}{2} \geq \sqrt[]{ab}](https://lms.umb.sk/filter/tex/pix.php/3823335945f2c477e45275ee236ecc9a.png) ,
, 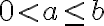
prepíšeme do ekvivalentnej formy![( \sqrt[]{a} -\sqrt[]{b} )^2 \geq 0 ( \sqrt[]{a} -\sqrt[]{b} )^2 \geq 0](https://lms.umb.sk/filter/tex/pix.php/a57aba5d980bcbbc8707ba2386f365e7.png) ,
,
ktorá je pravdivým výrokom pre ľubovoľné dve reálne čísla. Pre stredoškolákov je prijateľná aj geometrická verzia tohto dôkazu, kde sa využíva Euklidova veta o výške.
Uvažujme pravouhlý trojuholník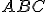 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole 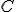 . Nech Tálesova polkružnica zostrojená nad preponou
. Nech Tálesova polkružnica zostrojená nad preponou 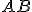 (obrázok)
má polomer
(obrázok)
má polomer 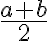 a nech
a nech 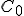 je bod, pre ktorý platí
je bod, pre ktorý platí 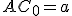 a
a 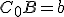 . Kolmica k prepone
. Kolmica k prepone 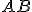 prechádzajúca bodom
prechádzajúca bodom 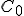 je zrejme výška trojuholníka
je zrejme výška trojuholníka 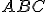 pretínajúca Tálesovu polkružnicu v bode
pretínajúca Tálesovu polkružnicu v bode 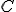 .
Trojuholníky
.
Trojuholníky 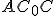 a
a 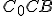 sú podobné, preto platí
sú podobné, preto platí 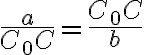 .
Odtiaľ následne
.
Odtiaľ následne ![\small C_0C= \sqrt[]{ab} \small C_0C= \sqrt[]{ab}](https://lms.umb.sk/filter/tex/pix.php/b24d7f62d875aafee45e7afc2818d798.png) . Jednoznačne
. Jednoznačne ![\sqrt[]{ab} \leq \sqrt[]{ab} \leq](https://lms.umb.sk/filter/tex/pix.php/7dc04aac6b5667533b4f69b9baec34ce.png) polomer kružnice
polomer kružnice 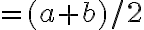 .
Rovnosť nastane len ak platí
.
Rovnosť nastane len ak platí 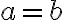 resp.
resp. 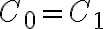 .
.
Otvorte si applet Tu
- Pre
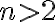 môžeme využiť nasledovný dôkaz:
môžeme využiť nasledovný dôkaz:
Geometrický priemer čísel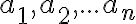 označme
označme ![z= \sqrt[n]{a_1 a_2 ... a_n} z= \sqrt[n]{a_1 a_2 ... a_n}](https://lms.umb.sk/filter/tex/pix.php/a06f35a0b9036015aa798638b790972b.png) , ďalej označme
, ďalej označme
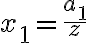 ,
, 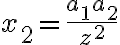 , ...,
, ..., 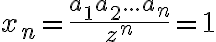
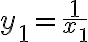 ,
, 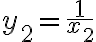 , ...,
, ..., 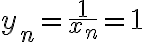
Pretože sú n-tice opačne usporiadané, platí nasledujúca nerovnosť, do ktorej rovno čísla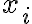 ,
, 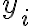 dosadíme a ekvivalentne upravíme:
dosadíme a ekvivalentne upravíme:
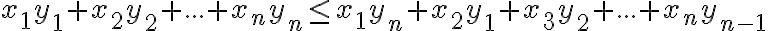 ,
,
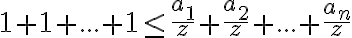 ,
,
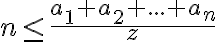
![z= \sqrt[n]{a_1a_2...a_n} \leq \frac{a_1+a_2+...a_n}{n} z= \sqrt[n]{a_1a_2...a_n} \leq \frac{a_1+a_2+...a_n}{n}](https://lms.umb.sk/filter/tex/pix.php/7daee894bfd6149219efdb1836e0f7fa.png)
Tým je AG-nerovnosť pre čísla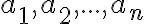 dokázaná.
dokázaná.
![\sqrt[n]{a_1 \cdot a_2 \cdots a_n} \leq \large \frac{a_1 + a_2 + \cdots + a_n}{n} \sqrt[n]{a_1 \cdot a_2 \cdots a_n} \leq \large \frac{a_1 + a_2 + \cdots + a_n}{n}](https://lms.umb.sk/filter/tex/pix.php/ec67f0d94807f647707b43ce6b5c4332.png)
