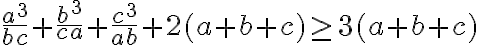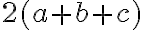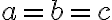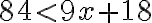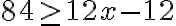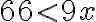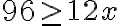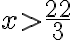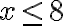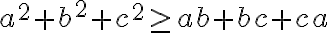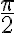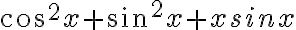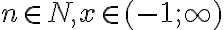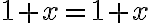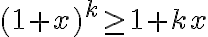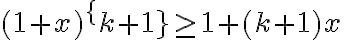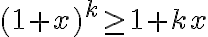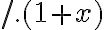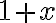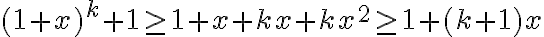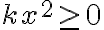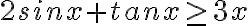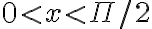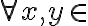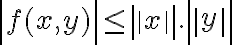Kupcová, Ľ.: Nerovnosti a nerovnice
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Kupcová, Ľ.: Nerovnosti a nerovnice |
| Vytlačil(a): | Gast |
| Dátum: | streda, 3 júla 2024, 13:37 |
Úvod
Pri riešení nerovníc na základnej resp. na strednej škole si musíme uvedomiť zásadný rozdiel medzi pojmami nerovnosť a nerovnica.
- Nerovnosť je vzťah medzi dvoma výrazmi, ktorý sa používa na porovnanie dvoch hodnôt (čísel) v istom usporiadaní (napr. podľa ich veľkosti). Príklady nerovností
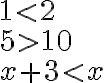 Posledná nerovnosť obsahuje premennú:
Posledná nerovnosť obsahuje premennú: - Nerovnica je algebraická úloha, pri ktorej sa hľadajú (najčastejšie všetky) čísla danej množiny, ktoré spĺňajú danú nerovnosť. Nerovnica je otázka formulovaná ako nerovnosť medzi dvoma výrokovými formami (napr. medzi dvoma algebraickými výrazmi). Príklady nerovníc.
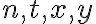 .
.
 .
.
Poznámky.
- Vyhodnotiť vzťah nerovnosti znamená určiť pravdivostnú hodnotu daného výroku.
- Riešenie nerovnosti znamená nájsť hodnoty premenných používaných v nerovnosti, ktoré po dosadení do príslušných výrokových foriem robia danú nerovnosť pravdivým výrokom. Tieto premenné sa nazývajú neznáme (okrem nich môžu existovať aj parametre). Najjednoduchšie nerovnosti sa riešia ich premenou na jednoduchšie ale zároveň rovnocenné nerovnice. Pozrite si nasledujúci príklad.
Príklad
Riešte nerovnicu v obore reálnych čísel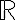
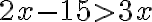 .
.
Riešenie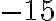 , čo zvykneme zapisovať pomocou intervalu
, čo zvykneme zapisovať pomocou intervalu 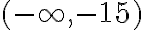 .
.
Riešte nerovnicu v obore reálnych čísel
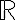
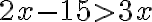 .
.
Riešenie
- pripočítajme k obidvom stranám nerovnice číslo 15, dostaneme jednoduchšiu nerovnicu
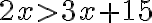
- odpočítajme od oboch strán výraz
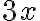 , dostaneme nerovnicu
, dostaneme nerovnicu
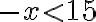
- vynásobením oboch strán nerovnosti číslom
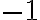 sa zmení znak nerovnosti a dostaneme nerovnicu
sa zmení znak nerovnosti a dostaneme nerovnicu
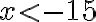
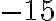 , čo zvykneme zapisovať pomocou intervalu
, čo zvykneme zapisovať pomocou intervalu 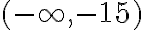 .
.
...
Ekvivalentné úpravy
Pri riešení rovníc a nerovníc v školskej matematike sa žiaci stretávajú predovšetkým s implikačnými a ekvivalentnými metódami riešenia. Implikačná úprava sa nazýva aj dôsledková úprava. V niektorých prípadoch sa pri riešení s výhodou použije aj experimentovanie. Ide predovšetkým o prípady, keď výroková forma vystupujúca v nerovnici nemá charakter kvadratickej (lineárnej) formy. Napríklad v úlohe:
Riešenie
Pri riešení postupujeme tak, že postupne dosadíme čísla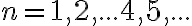 . Ľahko zistíme, že čísla 2,3,4 vyhovujú danej nerovnici (sú jej riešením) a čísla
. Ľahko zistíme, že čísla 2,3,4 vyhovujú danej nerovnici (sú jej riešením) a čísla 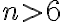 nie sú riešením v množine
nie sú riešením v množine  . Využitím programov GeoGebra a Excel môžeme experimentálne overiť toto tvrdenie na dostatočne veľkom počte prirodzených čísel.
. Využitím programov GeoGebra a Excel môžeme experimentálne overiť toto tvrdenie na dostatočne veľkom počte prirodzených čísel.
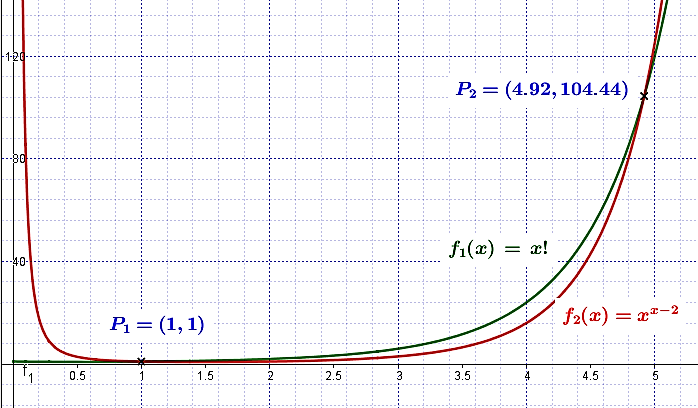
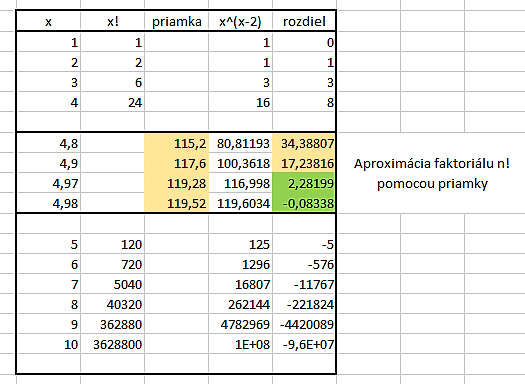
Otvorte konštrukciu TuOtvorte tabuľku Excel Tu
Pri riešení postupujeme tak, že postupne dosadíme čísla
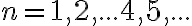 . Ľahko zistíme, že čísla 2,3,4 vyhovujú danej nerovnici (sú jej riešením) a čísla
. Ľahko zistíme, že čísla 2,3,4 vyhovujú danej nerovnici (sú jej riešením) a čísla 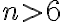 nie sú riešením v množine
nie sú riešením v množine  . Využitím programov GeoGebra a Excel môžeme experimentálne overiť toto tvrdenie na dostatočne veľkom počte prirodzených čísel.
. Využitím programov GeoGebra a Excel môžeme experimentálne overiť toto tvrdenie na dostatočne veľkom počte prirodzených čísel.
Otvorte konštrukciu TuOtvorte tabuľku Excel Tu
Nerovnica
- Nerovnica je úloha, v ktorej treba nájsť všetky prvky
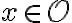 spĺňajúce nerovnosť
spĺňajúce nerovnosť 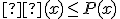 .
Množinu
.
Množinu  nazývame obor nerovnice.
nazývame obor nerovnice. - Výraz
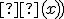 nazývame ľavá strana nerovnice, výraz
nazývame ľavá strana nerovnice, výraz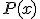 nazývame pravá strana nerovnice.
nazývame pravá strana nerovnice. - Definičný obor nerovnice
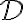 je podmnožina množiny
je podmnožina množiny  , v ktorej majú všetky výrazy v nerovnici zmysel.
, v ktorej majú všetky výrazy v nerovnici zmysel. - Množina riešení
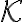 je množina všetkých tých prvkov množiny
je množina všetkých tých prvkov množiny 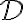 , ktoré spĺňajú danú nerovnosť.
, ktoré spĺňajú danú nerovnosť.
Ekvivalentné úpravy nerovníc
- Nahradenie ľubovoľnej strany nerovnice výrazom, ktorý sa jej na celej množine
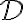 rovná.
rovná. - Pripočítanie výrazu, ktorý je definovaný v celom definičnom obore nerovnice
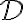 , k obidvom stranám nerovnice.
, k obidvom stranám nerovnice. - Vynásobenie obidvoch strán nerovnice výrazom, ktorý v celom obore nerovnice
 nadobúda kladné hodnoty. Vynásobenie obidvoch strán nerovnice výrazom,
ktorý v celom definičnom obore nerovnice
nadobúda kladné hodnoty. Vynásobenie obidvoch strán nerovnice výrazom,
ktorý v celom definičnom obore nerovnice  nadobúda záporné hodnoty a súčasne obrátenie znaku nerovnosti.
nadobúda záporné hodnoty a súčasne obrátenie znaku nerovnosti. - Umocnenie resp. odmocnenie obidvoch strán nerovnice na druhú, štvrtú atď., ak obidve strany nerovnice nadobúdajú v celom definičnom obore nerovnice nezáporné hodnoty..
- Nepárne umocnenie a odmocnenie oboch strán nerovnice.
___________________________________________________________________________
1) je to číselná množina, v ktorej hľadáme prvky spĺňajúce danú nerovnosť; pre naše účely bude to množinam reálnych čísel
je to číselná množina, v ktorej hľadáme prvky spĺňajúce danú nerovnosť; pre naše účely bude to množinam reálnych čísel
1)
 je to číselná množina, v ktorej hľadáme prvky spĺňajúce danú nerovnosť; pre naše účely bude to množinam reálnych čísel
je to číselná množina, v ktorej hľadáme prvky spĺňajúce danú nerovnosť; pre naše účely bude to množinam reálnych čísel
Známe nerovnosti
Nech 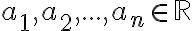 sú ľubovoľné reálne čísla. Potom platia nerovnosti:
sú ľubovoľné reálne čísla. Potom platia nerovnosti:
Harmonický priemer
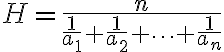
Geometrický priemer
![G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n} G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n}](https://lms.umb.sk/filter/tex/pix.php/a0b7c9933d767be06644db47123ab630.png)
Aritmetický priemer
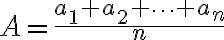
Kvadratický priemer
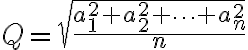
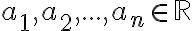 sú ľubovoľné reálne čísla. Potom platia nerovnosti:
sú ľubovoľné reálne čísla. Potom platia nerovnosti:
Harmonický priemer
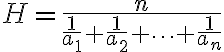
Geometrický priemer
![G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n} G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n}](https://lms.umb.sk/filter/tex/pix.php/a0b7c9933d767be06644db47123ab630.png)
Aritmetický priemer
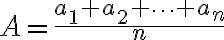
Kvadratický priemer
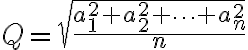
Dôkaz matematickou indukciou:
- Pre
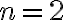 dôkaz je prijateľný na úrovni 1. ročníka strednej škola. Použijeme najskôr algebraické úpravy, pričom nerovnosť aritmetického a geometrického priemeru
dôkaz je prijateľný na úrovni 1. ročníka strednej škola. Použijeme najskôr algebraické úpravy, pričom nerovnosť aritmetického a geometrického priemeru
![\frac{a+b}{2} \geq \sqrt[]{ab} \frac{a+b}{2} \geq \sqrt[]{ab}](https://lms.umb.sk/filter/tex/pix.php/3823335945f2c477e45275ee236ecc9a.png) ,
, 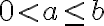
prepíšeme do ekvivalentnej formy![( \sqrt[]{a} -\sqrt[]{b} )^2 \geq 0 ( \sqrt[]{a} -\sqrt[]{b} )^2 \geq 0](https://lms.umb.sk/filter/tex/pix.php/a57aba5d980bcbbc8707ba2386f365e7.png) ,
,
ktorá je pravdivým výrokom pre ľubovoľné dve reálne čísla. Pre stredoškolákov je prijateľná aj geometrická verzia tohto dôkazu, kde sa využíva Euklidova veta o výške.
Uvažujme pravouhlý trojuholník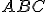 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole 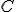 . Nech Tálesova polkružnica zostrojená nad preponou
. Nech Tálesova polkružnica zostrojená nad preponou 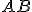 (obrázok)
má polomer
(obrázok)
má polomer 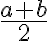 a nech
a nech 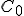 je bod, pre ktorý platí
je bod, pre ktorý platí 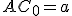 a
a 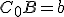 . Kolmica k prepone
. Kolmica k prepone 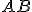 prechádzajúca bodom
prechádzajúca bodom 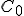 je zrejme výška trojuholníka
je zrejme výška trojuholníka 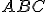 pretínajúca Tálesovu polkružnicu v bode
pretínajúca Tálesovu polkružnicu v bode 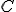 .
Trojuholníky
.
Trojuholníky 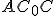 a
a 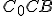 sú podobné, preto platí
sú podobné, preto platí 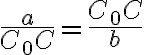 .
Odtiaľ následne
.
Odtiaľ následne ![\small C_0C= \sqrt[]{ab} \small C_0C= \sqrt[]{ab}](https://lms.umb.sk/filter/tex/pix.php/b24d7f62d875aafee45e7afc2818d798.png) . Jednoznačne
. Jednoznačne ![\sqrt[]{ab} \leq \sqrt[]{ab} \leq](https://lms.umb.sk/filter/tex/pix.php/7dc04aac6b5667533b4f69b9baec34ce.png) polomer kružnice
polomer kružnice 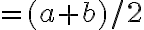 .
Rovnosť nastane len ak platí
.
Rovnosť nastane len ak platí 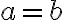 resp.
resp. 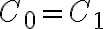 .
.
Otvorte si applet Tu
- Pre
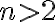 môžeme využiť nasledovný dôkaz:
môžeme využiť nasledovný dôkaz:
Geometrický priemer čísel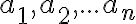 označme
označme ![z= \sqrt[n]{a_1 a_2 ... a_n} z= \sqrt[n]{a_1 a_2 ... a_n}](https://lms.umb.sk/filter/tex/pix.php/a06f35a0b9036015aa798638b790972b.png) , ďalej označme
, ďalej označme
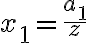 ,
, 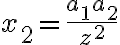 , ...,
, ..., 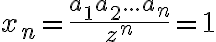
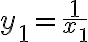 ,
, 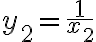 , ...,
, ..., 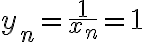
Pretože sú n-tice opačne usporiadané, platí nasledujúca nerovnosť, do ktorej rovno čísla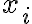 ,
, 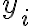 dosadíme a ekvivalentne upravíme:
dosadíme a ekvivalentne upravíme:
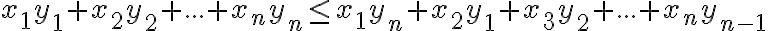 ,
,
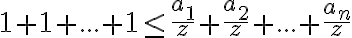 ,
,
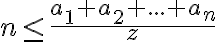
![z= \sqrt[n]{a_1a_2...a_n} \leq \frac{a_1+a_2+...a_n}{n} z= \sqrt[n]{a_1a_2...a_n} \leq \frac{a_1+a_2+...a_n}{n}](https://lms.umb.sk/filter/tex/pix.php/7daee894bfd6149219efdb1836e0f7fa.png)
Tým je AG-nerovnosť pre čísla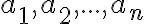 dokázaná.
dokázaná.
Lineárne nerovnice
Vyriešte nerovnicu:
Vyriešte nerovnicu:
Kvadratické nerovnice
Pri riešení kvadratických nerovníc v obore reálnych čísel často používame tzv. intervalovú metódu, ktorú popíšeme jednoduchým algoritmom.
- Na jednej strane nerovnice „vyrobíme“ nulu, ak je nula už v zadaní postúpime na ďalší krok.
- Nájdeme korene odpovedajúcej kvadratickej rovnice.
- Ak sú korene reálne čísla, tak nenulovú stranu nerovnice rozložíme na súčin dvoch dvojčlenov (nemusia byť nutne rôzne).
- V ďalšom riešení použijeme metódu nulových bodov.
- Ak neexistujú reálne korene, tak dosadíme nejaké číslo (napr. nulu) do nerovnice a zistíme, či vzniknutý výrok je pravdivý. Ak áno, tak nerovnici vyhovujú všetky reálne čísla. Ak nie, tak nerovnica nemá riešenie.
Vyriešte nerovnicu:
Vyriešte nerovnicu:
IKT - grafické riešenie
Čínske príslovie o vzdelávaní:
„Ak mi niečo vysvetlíš - zabudnem, ak mi to ukážeš - zapamätám si, ale ak to urobím - pochopím “
„Ak mi niečo vysvetlíš - zabudnem, ak mi to ukážeš - zapamätám si, ale ak to urobím - pochopím “
Fáza vyučovacej hodiny: precvičovanie, upevňovanie a aplikácia prebratého učiva
Možnosti pri riešení kvadratických nerovníc
Stiahnite si applet Tu
- klasické žiacke riešenia na tabuli resp. v zošitoch
- využívanie vhodných informačných a komunikačných technológií,
- ukážka použitia GeoGebry
Stiahnite si applet Tu
Cvičenie.
Vytvorte si applet (zbierku riešených úloh), ktorý využujete pri riešení nerovníc buď na základnej škole alebo na strednej škole. Stiahnite si ukážku Tu
Vytvorte si applet (zbierku riešených úloh), ktorý využujete pri riešení nerovníc buď na základnej škole alebo na strednej škole. Stiahnite si ukážku Tu
Lineárna nerovnica s neznámou v menovateli
Vyriešte nerovnicu:
Poznámka
Vhodná metóda na riešenie nerovníc je metóda nulových bodov. Je to jednoduchá a „bezpečná“ metóda.
Vhodná metóda na riešenie nerovníc je metóda nulových bodov. Je to jednoduchá a „bezpečná“ metóda.
Vyriešte nerovnicu:
Lineárna nerovnica s neznámou v absolútnej hodnote
Vyriešte nerovnicu:
Vyriešte nerovnicu:
Nerovnice v praxi
1) Ak traktorista zorie denne o 2 ha viac, zorie 84 ha parcelu za menej ako 9 dní. Ak by zoral o 1 ha menej, zoral by tú istú parcelu najskôr za 12 dní. V akých hraniciach sa pohybuje jeho priemerný denný výkon?
Riešenie:
(a) Označme x denný výkon traktoristu. Prvá podmienka v úlohe hovorí, že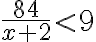 , druhá podmienka, že
, druhá podmienka, že 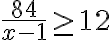 . Matematickým zápisom úlohy je sústava nerovníc
. Matematickým zápisom úlohy je sústava nerovníc 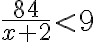 ,
, 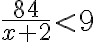 .
.
(b) Riešime zostavenú sústavu nerovníc. Vzhľadom na reálnu situáciu je zrejmé, že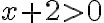 , aj
, aj 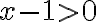 . Preto
. Preto
Riešenie:
(a) Označme x denný výkon traktoristu. Prvá podmienka v úlohe hovorí, že
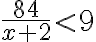 , druhá podmienka, že
, druhá podmienka, že 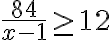 . Matematickým zápisom úlohy je sústava nerovníc
. Matematickým zápisom úlohy je sústava nerovníc 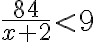 ,
, 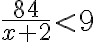 .
.(b) Riešime zostavenú sústavu nerovníc. Vzhľadom na reálnu situáciu je zrejmé, že
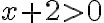 , aj
, aj 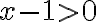 . Preto
. Preto
(c) Riešením danej reálnej situácie je interval 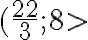 . Priemerný denný výkon traktoristu je väčší ako
. Priemerný denný výkon traktoristu je väčší ako 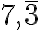 ha, ale nie väčší ako 8 ha.
ha, ale nie väčší ako 8 ha.
2) Podnik vyrába dva druhy výrobkov V1 a V2.
Oba druhy výrobkov sa vyrábajú zo surovín S1 a S2. Podnik
má k dispozícii 22 kg suroviny S1 a 28 kg suroviny S2. Na výrobu 1 ks výrobku V1 sa spotrebujú 2 kg
suroviny S1 a 4 kg suroviny S2. Na výrobu 1 ks výrobku V2 sú potrebné 3 kg
suroviny S1 a 2 kg suroviny S2. Zisk z predaja 1 ks výrobku V1 je 16 p.j. a z predaja
1 ks výrobku V2 12 p.j. Aké množstvo výrobkov V1 a V2 má
podnik vyrobiť, aby dosiahol maximálny zisk?
a) zápis:
b) riešenie:
a) zápis:
b) riešenie:
c) Odpoveď: Aby podnik dosiahol maximálny zisk, musí (pri daných podmienkach) vyrobiť 4 výrobky V1 a 5 výrobkov V2, pričom zisk podniku je 128 p.j.

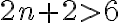
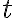
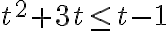
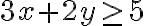
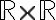
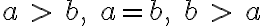
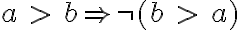
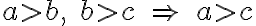
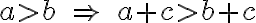
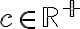
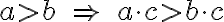
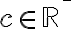
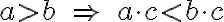

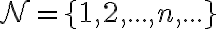
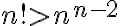
![\sqrt[n]{a_1 \cdot a_2 \cdots a_n} \leq \large \frac{a_1 + a_2 + \cdots + a_n}{n} \sqrt[n]{a_1 \cdot a_2 \cdots a_n} \leq \large \frac{a_1 + a_2 + \cdots + a_n}{n}](https://lms.umb.sk/filter/tex/pix.php/ec67f0d94807f647707b43ce6b5c4332.png)
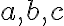
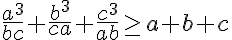
![\frac{a^3}{bc} + b+ c \geq 3 \sqrt[3]{ \frac{a^3}{bc} . b. c} = 3a \frac{a^3}{bc} + b+ c \geq 3 \sqrt[3]{ \frac{a^3}{bc} . b. c} = 3a](https://lms.umb.sk/filter/tex/pix.php/54e45fc77edbd47b8c2012b7f8704c89.png)
![\frac{b^3}{ca} + c+ a \geq 3 \sqrt[3]{ \frac{b^3}{ca} . c. a} = 3b \frac{b^3}{ca} + c+ a \geq 3 \sqrt[3]{ \frac{b^3}{ca} . c. a} = 3b](https://lms.umb.sk/filter/tex/pix.php/0d0c652075fd96a34a43cd6b90ae2d71.png)
![\frac{c^3}{ab} + a+ b \geq3 \sqrt[n]{\frac{b^3}{ca} . c. a} = 3c \frac{c^3}{ab} + a+ b \geq3 \sqrt[n]{\frac{b^3}{ca} . c. a} = 3c](https://lms.umb.sk/filter/tex/pix.php/f17ab203cd0027eaaeebd2549bfeb4af.png)