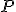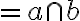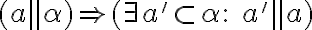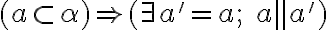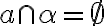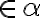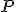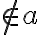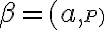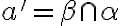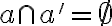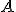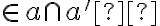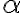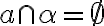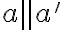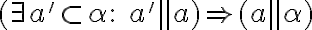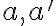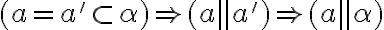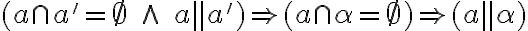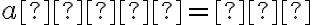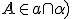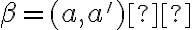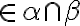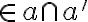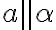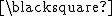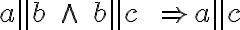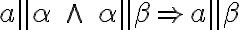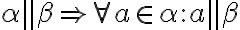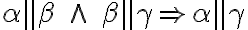Stereometrické vzťahy
Rovnobežnosť útvarov
Definície - rovnobežnosť
- Priamky
 sú navzájom rovnobežné práve vtedy, ak
sú navzájom rovnobežné práve vtedy, ak 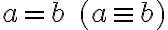 alebo existuje rovina, v ktorej obe priamky ležia a nemajú žiaden spoločný bod.
alebo existuje rovina, v ktorej obe priamky ležia a nemajú žiaden spoločný bod.
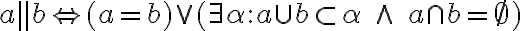
- Priamka
 je rovnobežná s rovinou
je rovnobežná s rovinou  práve vtedy, ak priamka
práve vtedy, ak priamka  leží v rovine α alebo s ňou nemá žiaden spoločný bod.
leží v rovine α alebo s ňou nemá žiaden spoločný bod.
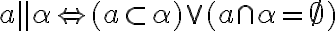
- Dve roviny
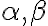 sú navzájom rovnobežné práve vtedy, ak: alebo α = β alebo tieto roviny nemajú žiaden spoločný bod.
sú navzájom rovnobežné práve vtedy, ak: alebo α = β alebo tieto roviny nemajú žiaden spoločný bod.
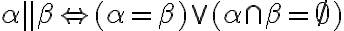
Poznámky
- Dve priamky sú rovnobežné, alebo rôznobežné, alebo mimobežné.
- Priamka je s rovinou rovnobežná, alebo rôznobežná.
- Dve roviny sú rovnobežné, alebo rôznobežné.
Kritérium rovnobežnosti priamky a roviny
Priamka je rovnobežná s rovinou
je rovnobežná s rovinou  práve vtedy, ak je rovnobežná s aspoň jednou priamkou
práve vtedy, ak je rovnobežná s aspoň jednou priamkou 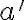 roviny
roviny  (
(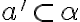 ). Symbolicky
). Symbolicky
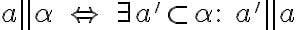 .
.
Priamka
 je rovnobežná s rovinou
je rovnobežná s rovinou  práve vtedy, ak je rovnobežná s aspoň jednou priamkou
práve vtedy, ak je rovnobežná s aspoň jednou priamkou 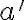 roviny
roviny  (
(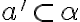 ). Symbolicky
). Symbolicky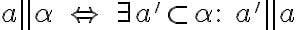 .
.
Dôkaz
- pri dokazovaní využijeme dichotomický princíp vzhľadom na prienik priamky  a roviny
a roviny 
 a roviny
a roviny 
Dôkazy týchto tvrdení nájdete v práci Klenková: Stereometria. Na cvičení ich budete prezentovať.
Kritérium rovnobežnosti dvoch rovín
Dve roviny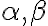 sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky
sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky 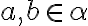 , ktoré sú rovnobežné s druhou rovinou
, ktoré sú rovnobežné s druhou rovinou 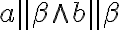 . Symbolicky
. Symbolicky
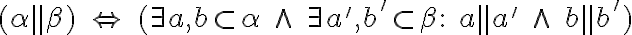 .
.
Dve roviny
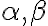 sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky
sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky 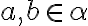 , ktoré sú rovnobežné s druhou rovinou
, ktoré sú rovnobežné s druhou rovinou 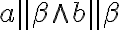 . Symbolicky
. Symbolicky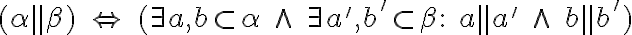 .
.
Dôkaz
- Nutná podmienka -
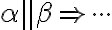 . Môžu nastať dva prípady:
. Môžu nastať dva prípady:
-
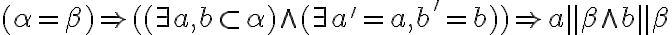 .
. 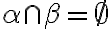 : Potom existujú rôznobežky
: Potom existujú rôznobežky 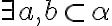 , pre ktoré platí
, pre ktoré platí
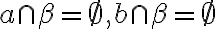 . Ak by tieto prieniky neboli prázdne množiny, tak by aj
. Ak by tieto prieniky neboli prázdne množiny, tak by aj 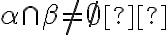 ,
čo je spor s predpokladom.
,
čo je spor s predpokladom.
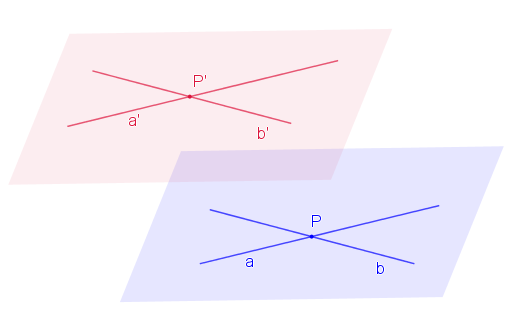 Otvorte si applet Tu
Otvorte si applet Tu
-
- postačujúca podmienka -
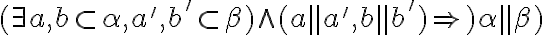
- Ak
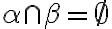 , tak
, tak 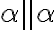 .
. - Ak
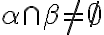 a nech existujú rôznobežky (predpokad)
a nech existujú rôznobežky (predpokad) 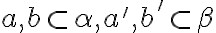 . Potom roviny majú spoločnú priamku
. Potom roviny majú spoločnú priamku  :
: 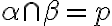 ,
,
ktorá pretína aspoň jednu rôznobežku (môže byť rovnobežná najviac s jednou z nich).
Nech je to priamka
(môže byť rovnobežná najviac s jednou z nich).
Nech je to priamka  ; označme
; označme 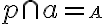 . To ale znamená, že bod
. To ale znamená, že bod 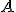 by ležal
v rovine
by ležal
v rovine 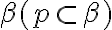 a bol by i spoločným bodom priamky
a bol by i spoločným bodom priamky  s rovinou
s rovinou 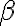 .
Je to spor s predpokladom
.
Je to spor s predpokladom 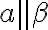 .
.
- Ak
... ...