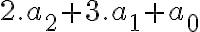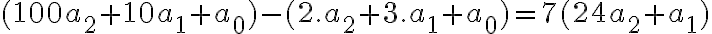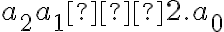Číselné sústavy
Zadanie
Riešenia - deliteľnosť
Deliteľnosť
- Ak pre trojciferné čísla
 platí
platí
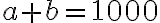 , tak sa čísla
, tak sa čísla
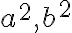 zhodujú v poslednom trojčíslí. Dokážte to.
zhodujú v poslednom trojčíslí. Dokážte to. - počítajme
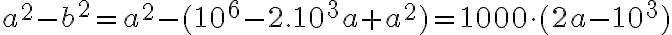 , odkiaľ vyplýva
, odkiaľ vyplýva - rozdiel druhých mocnín je násobkom čísla
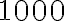 Čísla
Čísla
- V čísle
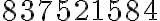 vyškrtnite 4 číslice tak, aby ste dostali 5-ciferné číslo deliteľné číslami 9 a 5. Nájdite všetky možnosti.
vyškrtnite 4 číslice tak, aby ste dostali 5-ciferné číslo deliteľné číslami 9 a 5. Nájdite všetky možnosti. - zrejme musíme škrtnúť posledné dve cifry 8,4, aby číslo bolo deliteľné 5
- zostávajúce cifry dávajú súčet 31, z ktorého musíme odpočítať súčet niektorých cifier, aby bol deliteľný 9
- to je možné napríklad pre súčet 8+5=13, v tom prípade ciferný súčet ostávajúceho čísla bude 18
- alebo pre súčet 7+5+1=13 resp. pre 3+7+2+1=13
Požiadavke v zadaní vyhovujú čísla 37 215, 8 325, 855.
- V čísle
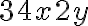 doplňte za
doplňte za
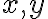 cifry tak, aby vzniknuté číslo bolo deliteľné číslom 3 a 4. Nájdite všetky riešenia.
cifry tak, aby vzniknuté číslo bolo deliteľné číslom 3 a 4. Nájdite všetky riešenia. - posledné dvojčísle musí byť deliteľné 4, odkiaľ dostávame
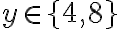 , nulou nemôže končiť lebo by bolo len dvojciferné
, nulou nemôže končiť lebo by bolo len dvojciferné - po dosadení za
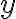 skúmame ešte požiadavku deliteľnosti
skúmame ešte požiadavku deliteľnosti
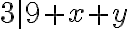 , preto
, preto
![[x,y] \in \lbrace{[2,4],[5,4],[8,4],[1,8],[4,8],[7,8]}\rbrace [x,y] \in \lbrace{[2,4],[5,4],[8,4],[1,8],[4,8],[7,8]}\rbrace](https://lms.umb.sk/filter/tex/pix.php/2cc05da9d341d82064eb03d0b6855d0f.png) Požiadavke v zadaní vyhovujú čísla 34
224, ..., 34 128, ...
Požiadavke v zadaní vyhovujú čísla 34
224, ..., 34 128, ...
- Dokážte, že štvorec nepárneho čísla po delení číslom 8 dáva zvyšok 1.
- Nájdite celé číslo
 a cifru
a cifru
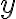 tak, aby platilo
tak, aby platilo
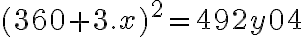 .
Návod: Využite, že ľavá strana danej rovnice je deliteľná číslom 9.
Výsledok: cifra
.
Návod: Využite, že ľavá strana danej rovnice je deliteľná číslom 9.
Výsledok: cifra -
Nech číslo
 má v desiatkovej číselnej sústave zápis
má v desiatkovej číselnej sústave zápis
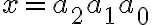 . Ukážte, že 7 delí práve vtedy,
. Ukážte, že 7 delí práve vtedy,
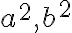 sa zhodujú v poslednom trojčíslí.
sa zhodujú v poslednom trojčíslí.
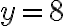 a číslo
a číslo
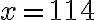 alebo
alebo
 .
.