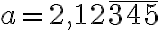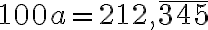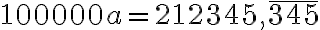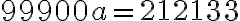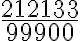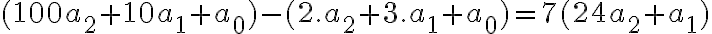Číselné sústavy
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Číselné sústavy |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | štvrtok, 2 mája 2024, 05:44 |
Zadanie
Číselné sústavy
-
Vypočítajte
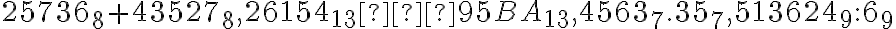 .
. - Doplňte miesto hviezdičiek číslice tak, aby výsledok bol správny:
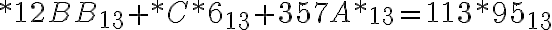 .
. - Trojciferné číslo zapísané v deviatkovej sústave je zakončené číslicou
 . Ak ju presunieme na prvé miesto dostaneme číslo, ktoré je v deviatkovej sústave o
. Ak ju presunieme na prvé miesto dostaneme číslo, ktoré je v deviatkovej sústave o
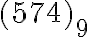 menšie ako pôvodné. Určte pôvodné číslo.
menšie ako pôvodné. Určte pôvodné číslo. - Ak medzi číslice dvojciferného čísla vpíšeme číslicu
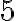 , tak dostaneme
, tak dostaneme
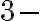 ciferné číslo, ktoré je o
ciferné číslo, ktoré je o
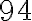 väčšie, ako
väčšie, ako
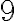 násobok daného čísla. Nájdite ho.
násobok daného čísla. Nájdite ho. - Nájdite všetky trojciferné čísla s touto vlastnosťou: ak vyškrtneme v čísle jeho prostrednú cifru a vzniknuté dvojciferné číslo vynásobíme druhou mocninou vyškrtnutej cifry,
dostaneme opäť pôvodné trojciferné číslo. (MO, roč. 2018/19, kat. B) - Nájdite v desiatkovej číselnej sústave aspoň tri dvojice trojciferných čísel väčších ako
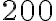 a zároveň menších ako
a zároveň menších ako
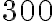 , ktorých súčet v
, ktorých súčet v
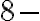 číselnej sústave má zápis
číselnej sústave má zápis
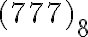 .Uvádzame jednu dvojicu:
.Uvádzame jednu dvojicu:
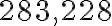 , ktorá spĺňa požiadavky, lebo
, ktorá spĺňa požiadavky, lebo
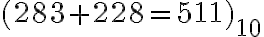 a zároveň
a zároveň
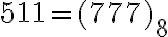
- Určte racionálne číslo
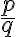 tak, aby jeho rozvoj v desiatkovej sústave mal tvar
tak, aby jeho rozvoj v desiatkovej sústave mal tvar
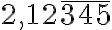 .
Deliteľnosť
.
Deliteľnosť
- Ak pre trojciferné čísla
 platí
platí
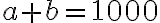 , tak sa čísla
, tak sa čísla
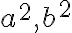 zhodujú v poslednom trojčíslí. Dokážte to.
zhodujú v poslednom trojčíslí. Dokážte to. - V čísle
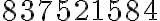 vyškrtnite 4 číslice tak, aby ste dostali 5-ciferné číslo deliteľné číslami 9 a 5. Nájdite všetky možnosti.
vyškrtnite 4 číslice tak, aby ste dostali 5-ciferné číslo deliteľné číslami 9 a 5. Nájdite všetky možnosti. - V čísle
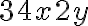 doplňte za
doplňte za
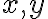 cifry tak, aby vzniknuté číslo bolo deliteľné číslom 3 a 4. Nájdite všetky riešenia.
cifry tak, aby vzniknuté číslo bolo deliteľné číslom 3 a 4. Nájdite všetky riešenia. - Dokážte, že štvorec nepárneho čísla po delení číslom 8 dáva zvyšok 1.
- Nájdite celé číslo
 a cifru
a cifru
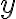 tak, aby platilo
tak, aby platilo
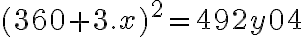 .
Návod: Využite, že ľavá strana danej rovnice je deliteľná číslom 9.
.
Návod: Využite, že ľavá strana danej rovnice je deliteľná číslom 9.
-
Nech číslo
 má v desiatkovej číselnej sústave zápis
má v desiatkovej číselnej sústave zápis
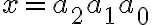 . Ukážte, že
. Ukážte, že
Úloha 1 a 2 - riešenie
-
Vypočítajte
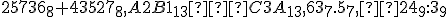 .
.
Počítajme-
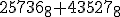 - sčítanie v 8-vej sústave:
- sčítanie v 8-vej sústave:
6 + 7 = (15)8 =1 . 8 + 5 ; 3 + 2 + 1 = 0 . 8 + 6 ; 7 + 5 + 0 = (14)8 = 1 . 8 + 4; 5 + 3 +1 = (10)8 = 1 . 8 + 0
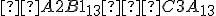 - odčítanie v 13-vej sústave:
- odčítanie v 13-vej sústave:
(1 + 13) - A = (4)13 ; B - (3 + 1) = 7 ; (2 + 13) - C = ...
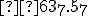 ... otvor súbor EXCEL Tu
... otvor súbor EXCEL Tu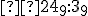
-
- Doplňte miesto hviezdičiek číslice tak, aby výsledok bol správny:
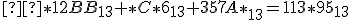 Počítajme v sústave o základe 13 (od "konca" sprava)
Počítajme v sústave o základe 13 (od "konca" sprava) - Súčet číslic nultého rádu
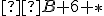 musí končiť číslicou 5. Keďže B má hodnotu 11 musí byť tento súčet rovný práve 25:
musí končiť číslicou 5. Keďže B má hodnotu 11 musí byť tento súčet rovný práve 25: 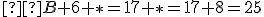 . Odkiaľ dostaneme, že
. Odkiaľ dostaneme, že 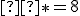 . Po dosadení a pri ďalšom sčitovaní číslic vyššieho rádu musíme pridať dva prechody cez desiatku, preto
. Po dosadení a pri ďalšom sčitovaní číslic vyššieho rádu musíme pridať dva prechody cez desiatku, preto - Súčet číslic nultého rádu
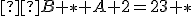 musí končiť číslicou 9. Preto táto druhá
musí končiť číslicou 9. Preto táto druhá 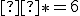 .
. - ...
Riešenia - sústavy
Príklad 3.
Trojciferné číslo zapísané v deviatkovej sústave je zakončené číslicou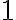 . Ak ju presunieme na prvé miesto dostaneme číslo, ktoré je v deviatkovej sústave o
. Ak ju presunieme na prvé miesto dostaneme číslo, ktoré je v deviatkovej sústave o
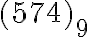 menšie ako pôvodné. Určte pôvodné číslo.
menšie ako pôvodné. Určte pôvodné číslo.
Riešenie.
Ak medzi číslice dvojciferného čísla vpíšeme číslicu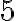 , tak dostaneme
, tak dostaneme
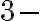 ciferné číslo, ktoré je o
ciferné číslo, ktoré je o
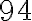 väčšie, ako
väčšie, ako
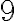 násobok daného čísla. Nájdite ho.
násobok daného čísla. Nájdite ho.
Riešenie.
Nájdite v desiatkovej číselnej sústave aspoň tri dvojice trojciferných čísel väčších ako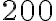 a zároveň menších ako
a zároveň menších ako
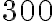 , ktorých súčet v
, ktorých súčet v
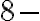 číselnej sústave má zápis
číselnej sústave má zápis
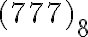 .Uvádzame jednu dvojicu:
.Uvádzame jednu dvojicu:
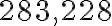 , ktorá spĺňa požiadavky, lebo
, ktorá spĺňa požiadavky, lebo
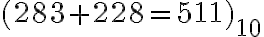 a zároveň
a zároveň
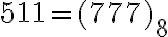
Riešenie.
Určte racionálne číslo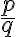 tak, aby jeho rozvoj v desiatkovej sústave mal tvar
tak, aby jeho rozvoj v desiatkovej sústave mal tvar
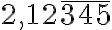 .
.
Riešenie.
Trojciferné číslo zapísané v deviatkovej sústave je zakončené číslicou
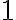 . Ak ju presunieme na prvé miesto dostaneme číslo, ktoré je v deviatkovej sústave o
. Ak ju presunieme na prvé miesto dostaneme číslo, ktoré je v deviatkovej sústave o
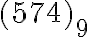 menšie ako pôvodné. Určte pôvodné číslo.
menšie ako pôvodné. Určte pôvodné číslo.
Riešenie.
- nech hľadané číslo má zápis v tvare
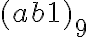 , potom má platiť
, potom má platiť
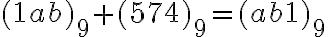
- po úprave dostávame
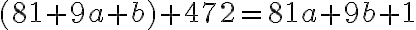 , čo je ekvivalentné s rovnicou
, čo je ekvivalentné s rovnicou
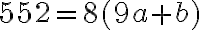
- posledná rovnica má v obore
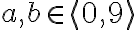 práve jedno riešenie
práve jedno riešenie
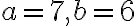 Riešením je číslo
Riešením je číslo
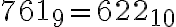 .
.
Ak medzi číslice dvojciferného čísla vpíšeme číslicu
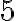 , tak dostaneme
, tak dostaneme
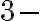 ciferné číslo, ktoré je o
ciferné číslo, ktoré je o
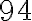 väčšie, ako
väčšie, ako
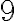 násobok daného čísla. Nájdite ho.
násobok daného čísla. Nájdite ho.
Riešenie.
- nech hľadané číslo má v desiatkovej číselnej sústave skrátený zápis v tvare
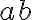 , kde
, kde
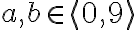
- potom musí platiť
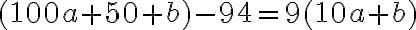 , čo je ekvivalentné s rovnicou
, čo je ekvivalentné s rovnicou
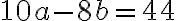 ; riešením je dvojica
; riešením je dvojica
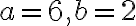 .
Hľadané číslo je
.
Hľadané číslo je
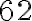 .
.
Nájdite v desiatkovej číselnej sústave aspoň tri dvojice trojciferných čísel väčších ako
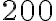 a zároveň menších ako
a zároveň menších ako
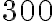 , ktorých súčet v
, ktorých súčet v
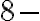 číselnej sústave má zápis
číselnej sústave má zápis
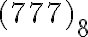 .Uvádzame jednu dvojicu:
.Uvádzame jednu dvojicu:
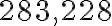 , ktorá spĺňa požiadavky, lebo
, ktorá spĺňa požiadavky, lebo
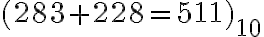 a zároveň
a zároveň
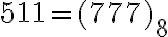
Riešenie.
- hľadané čísla
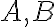 v desiatkovej číselnej sústave musia mať prvú cifru rovnú
v desiatkovej číselnej sústave musia mať prvú cifru rovnú
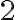 , teda ich skrátený zápis musí mať tvar
, teda ich skrátený zápis musí mať tvar
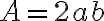
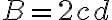
- vzhľadom na symetriu môžeme predpokladať, že
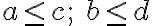 , zároveň musí platiť
Riešením sú napríklad dvojice čísel
, zároveň musí platiť
Riešením sú napríklad dvojice čísel
![[220,291];[222,289];[253,258] [220,291];[222,289];[253,258]](https://lms.umb.sk/filter/tex/pix.php/450ca171de141a8ed1151fcae818b40b.png) .
.
Určte racionálne číslo
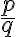 tak, aby jeho rozvoj v desiatkovej sústave mal tvar
tak, aby jeho rozvoj v desiatkovej sústave mal tvar
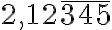 .
.
Riešenie.
Riešenia - deliteľnosť
Deliteľnosť
- Ak pre trojciferné čísla
 platí
platí
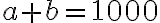 , tak sa čísla
, tak sa čísla
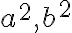 zhodujú v poslednom trojčíslí. Dokážte to.
zhodujú v poslednom trojčíslí. Dokážte to. - počítajme
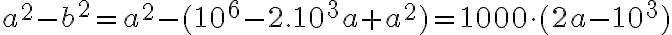 , odkiaľ vyplýva
, odkiaľ vyplýva - rozdiel druhých mocnín je násobkom čísla
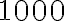 Čísla
Čísla
- V čísle
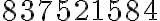 vyškrtnite 4 číslice tak, aby ste dostali 5-ciferné číslo deliteľné číslami 9 a 5. Nájdite všetky možnosti.
vyškrtnite 4 číslice tak, aby ste dostali 5-ciferné číslo deliteľné číslami 9 a 5. Nájdite všetky možnosti. - zrejme musíme škrtnúť posledné dve cifry 8,4, aby číslo bolo deliteľné 5
- zostávajúce cifry dávajú súčet 31, z ktorého musíme odpočítať súčet niektorých cifier, aby bol deliteľný 9
- to je možné napríklad pre súčet 8+5=13, v tom prípade ciferný súčet ostávajúceho čísla bude 18
- alebo pre súčet 7+5+1=13 resp. pre 3+7+2+1=13
Požiadavke v zadaní vyhovujú čísla 37 215, 8 325, 855.
- V čísle
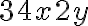 doplňte za
doplňte za
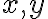 cifry tak, aby vzniknuté číslo bolo deliteľné číslom 3 a 4. Nájdite všetky riešenia.
cifry tak, aby vzniknuté číslo bolo deliteľné číslom 3 a 4. Nájdite všetky riešenia. - posledné dvojčísle musí byť deliteľné 4, odkiaľ dostávame
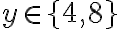 , nulou nemôže končiť lebo by bolo len dvojciferné
, nulou nemôže končiť lebo by bolo len dvojciferné - po dosadení za
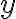 skúmame ešte požiadavku deliteľnosti
skúmame ešte požiadavku deliteľnosti
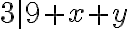 , preto
, preto
![[x,y] \in \lbrace{[2,4],[5,4],[8,4],[1,8],[4,8],[7,8]}\rbrace [x,y] \in \lbrace{[2,4],[5,4],[8,4],[1,8],[4,8],[7,8]}\rbrace](https://lms.umb.sk/filter/tex/pix.php/2cc05da9d341d82064eb03d0b6855d0f.png) Požiadavke v zadaní vyhovujú čísla 34
224, ..., 34 128, ...
Požiadavke v zadaní vyhovujú čísla 34
224, ..., 34 128, ...
- Dokážte, že štvorec nepárneho čísla po delení číslom 8 dáva zvyšok 1.
- Nájdite celé číslo
 a cifru
a cifru
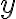 tak, aby platilo
tak, aby platilo
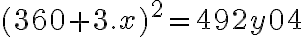 .
Návod: Využite, že ľavá strana danej rovnice je deliteľná číslom 9.
Výsledok: cifra
.
Návod: Využite, že ľavá strana danej rovnice je deliteľná číslom 9.
Výsledok: cifra -
Nech číslo
 má v desiatkovej číselnej sústave zápis
má v desiatkovej číselnej sústave zápis
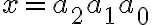 . Ukážte, že 7 delí práve vtedy,
. Ukážte, že 7 delí práve vtedy,
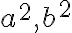 sa zhodujú v poslednom trojčíslí.
sa zhodujú v poslednom trojčíslí.
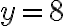 a číslo
a číslo
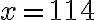 alebo
alebo
 .
.
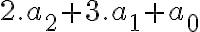
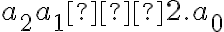

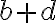
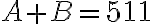
![[b=0,d=1],[b=2,d=9],[b=3,d=8],[b=4,d=7], ... [b=0,d=1],[b=2,d=9],[b=3,d=8],[b=4,d=7], ...](https://lms.umb.sk/filter/tex/pix.php/026d66ecb10bc3caf00d950886bc52a2.png)
![[b=0,d=1] [b=0,d=1]](https://lms.umb.sk/filter/tex/pix.php/a0bb5fc3ad685ae929ce5385b0d66ceb.png)
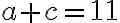
![[220,291];[230,281];[220,291];... [220,291];[230,281];[220,291];...](https://lms.umb.sk/filter/tex/pix.php/627fac48197ec31d5838a9564833c6a6.png)
![[b=2,d=9],[b=3,d=8],[b=4,d=7], ... [b=2,d=9],[b=3,d=8],[b=4,d=7], ...](https://lms.umb.sk/filter/tex/pix.php/633b4146a0ddf1997273529cab1a63e2.png)
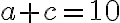
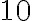
![[222,289];[243,268];... [222,289];[243,268];...](https://lms.umb.sk/filter/tex/pix.php/833fc146c297f356ea1ddeb26fd61990.png)