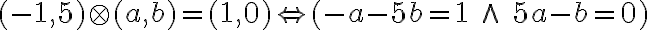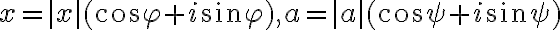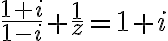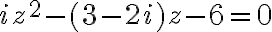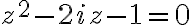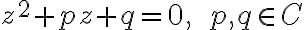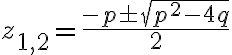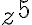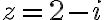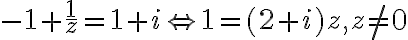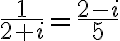Predchádzajúci

Komplexné čísla

Riešenie 3. až 7. úlohy

  1. Nájdite druhú odmocninu komplexného čísla resp. nájdite komplexný koreň rovnice x^2=a , ak x = |x| (cos \varphi + i sin \varphi), a = |a| (cos \psi + i sin \psi ) . 
  2. Riešte rovnice obore komplexných čísel
    • \frac{1+i}{1-i} + \frac{1}{z} =1+i
    • iz^2 - (3 - 2i) z - 6 = 0
    • z^2 - 2iz - 1 = 0.
  3. Ukážte, že korene kvadratickej rovnice z^2 + pz + q = 0,\ \ p,q \in C majú tvar z_{1,2} = \frac{-p \pm\sqrt{p^2-4q}} {2} .
  4. Nájdite inverzný prvok k číslu (-1,5) .
  5. Vypočítajte z^5 , ak z=2-i.
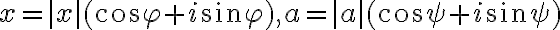  1. Nech x = |x| (cos \varphi + i sin \varphi), a = |a| (cos \psi + i sin \psi ) a nech je daná rovnica x^2=a .
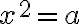    • Po dosadení a použitím Moivreovej vety dostaneme |x|^2 (cos\ 2\varphi + i sin\ 2\varphi)= |a| (cos\ \psi + i sin\ \psi )
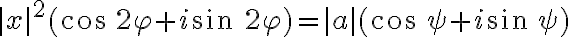
    • ľavá i pravá strana sú komplexné čísla, ktorá sa rovnajú práve vtedy, ak 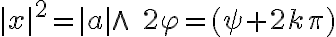|x|^2=|a| \wedge \ 2\varphi = (\psi +2k \pi) , odkiaľ
      dostávame riešenie: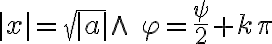 |x|=\sqrt {|a|} \wedge \ \varphi = \frac{\psi}{2} +k \pi .
  2. Najskôr upravme zlomok \frac{1+i}{1-i} = \frac{(1+i)^4}{(1-i)^2(1+i)^2}= \frac{(2i)^2}{4} =-1
    • tým sa pôvodná rovnica redukuje na tvar -1 + \frac{1}{z} =1+i \Leftrightarrow 1=(2+i)z, z \neq0 , odkiaľ
      dostávame riešenie: \frac{1}{2+i}=\frac{2-i}{5} .
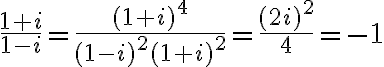
  3. Pozri v práci: Kvadratická rovnice a odmocnina z komplexního čísla. Tu.
  4. Riešte rovnicu (-1,5) \otimes (a, b)=(1,0) \Leftrightarrow (-a-5b=1\ \wedge \ 5a-b=0)
\( .\)
Predchádzajúci