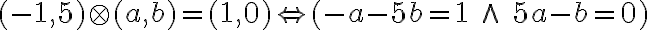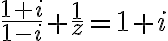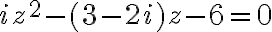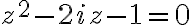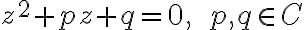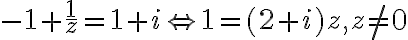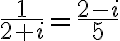Reálne a komplexné čísla
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Reálne a komplexné čísla |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 13:34 |
Opis
reálne čísla
Reálne čísla
-
Riešte
- V množine reálnych čísel riešte rovnicu
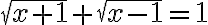 a nerovnicu
a nerovnicu
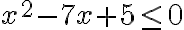 . Viac na www.príklady.com.
. Viac na www.príklady.com.
- Ak k číslam 2;7;17 pripočítame to isté reálne číslo, dostaneme prvé tri členy geometrickej postupnosti. Aké číslo sme pripočítali?
-
Ukážte, že
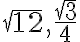 nie sú racionálne čísla.
nie sú racionálne čísla. - Vyjadrite graficky reálne čísla
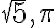 pomocou jednotkovej úsečky.
pomocou jednotkovej úsečky. -
Na obrázku je znázornená oblasť
 , ktorá vznikla z rovnostranného trojuholníka
, ktorá vznikla z rovnostranného trojuholníka
 s dĺžkou strany a vyrezaním štvorca vpísaného do vpísanej kružnice
s dĺžkou strany a vyrezaním štvorca vpísaného do vpísanej kružnice
 . Vypočítajte obsah oblasti
. Vypočítajte obsah oblasti
 .
.
Bača, M. a kol.: Zbierka riešených a neriešených úloh z matematiky. TU v Košiciach, 2011, str. 118. Dostupné Tu
Komplexné čísla
- Dokážte, že súčin dvoch komplexných čísel je rovný nule práve vtedy, ak je aspoň jeden z činiteľov je rovný nule.
- Pre súčin komplexných čísel vyjadrených v goniometrickom tvare platí vlastnosť komutatívnosti a asociatívnosti. Dokážte to použitím Moivrovej vety.
- Nájdite druhú odmocninu komplexného čísla resp. nájdite komplexný koreň rovnice
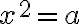 , ak
, ak
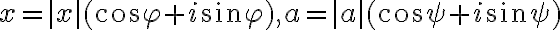 .
.
- Riešte rovnice obore komplexných čísel
-
Ukážte, že korene kvadratickej rovnice
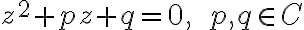 majú tvar
majú tvar
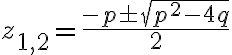 .
.
- Nájdite inverzný prvok k číslu
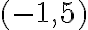 .
. - Vypočítajte
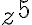 , ak
, ak
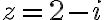 .
.
Riešenie 1. a 2. úlohy
Dokážte, že súčin dvoch komplexných čísel je rovný nule práve vtedy, ak je aspoň jeden z činiteľov je rovný nule.
-
Nech
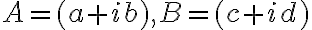 sú dve komplexné čísla vyjadrené v algebraickom tvare. Potom pre ich súčin platí
sú dve komplexné čísla vyjadrené v algebraickom tvare. Potom pre ich súčin platí
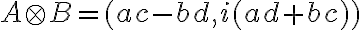 .
. -
Tento súčin je rovný nule, práve vtedy ak platí
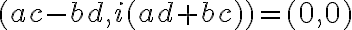 . Usporiadaná dvojica je rovná nule, práve vtedy, ak súčasne platia rovnosti
. Usporiadaná dvojica je rovná nule, práve vtedy, ak súčasne platia rovnosti
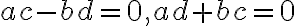 .
. -
Naša úloha sa zredukovala na riešenie sústavy dvoch rovníc o dvoch neznámych. Pri riešení stačí, keď prvú rovnicu vynásobíme číslom
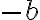 a druhú rovnicu číslom
a druhú rovnicu číslom
 . Po ich sčítaní dostaneme ...
. Po ich sčítaní dostaneme ...
Pre súčin komplexných čísel vyjadrených v goniometrickom tvare platí vlastnosť komutatívnosti a asociatívnosti. Dokážte to použitím Moivrovej vety.
Nech
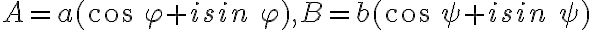 sú dve komplexné čísla vyjadrené v goniometrickom tvare a
sú dve komplexné čísla vyjadrené v goniometrickom tvare a 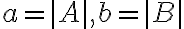 sú
absolútne hodnoty.
sú
absolútne hodnoty.
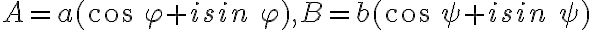 sú dve komplexné čísla vyjadrené v goniometrickom tvare a
sú dve komplexné čísla vyjadrené v goniometrickom tvare a 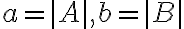 sú
absolútne hodnoty.
sú
absolútne hodnoty.
- Potom pre ich súčin platí
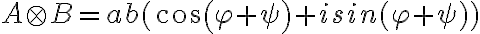 .
. - Vzhľadom na komutatívnosť sčítania v obore reálnych čísel, zrejme bude platiť
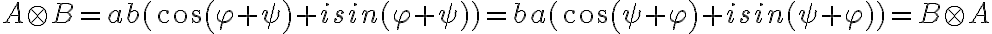 ,
,
čo je vlastnosť komutatívnosti súčinu komplexných čísel. - Podobne budeme postupovať pri asociatívnosti. Pri dokazovaní komutatívnosti a asociatívnosti sčítania komplexných čísel s výhodou použijeme algebraické tvary.
Riešenie 3. až 7. úlohy
-
Nech
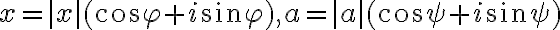 a nech je daná rovnica
a nech je daná rovnica
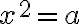 .
.
- Po dosadení a použitím Moivreovej vety dostaneme
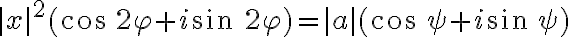
- ľavá i pravá strana sú komplexné čísla, ktorá sa rovnajú práve vtedy, ak
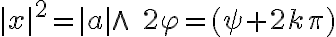 , odkiaľ
, odkiaľ
dostávame riešenie: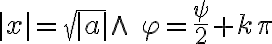 .
.
- Najskôr upravme zlomok
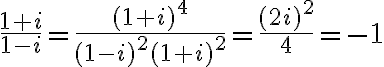
- Pozri v práci: Kvadratická rovnice a odmocnina z komplexního čísla. Tu.
- Riešte rovnicu