Reálne a komplexné čísla
reálne čísla
Komplexné čísla
Riešenie 1. a 2. úlohy
Dokážte, že súčin dvoch komplexných čísel je rovný nule práve vtedy, ak je aspoň jeden z činiteľov je rovný nule.
-
Nech
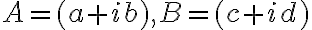 sú dve komplexné čísla vyjadrené v algebraickom tvare. Potom pre ich súčin platí
sú dve komplexné čísla vyjadrené v algebraickom tvare. Potom pre ich súčin platí
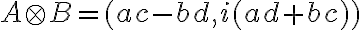 .
. -
Tento súčin je rovný nule, práve vtedy ak platí
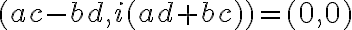 . Usporiadaná dvojica je rovná nule, práve vtedy, ak súčasne platia rovnosti
. Usporiadaná dvojica je rovná nule, práve vtedy, ak súčasne platia rovnosti
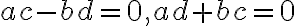 .
. -
Naša úloha sa zredukovala na riešenie sústavy dvoch rovníc o dvoch neznámych. Pri riešení stačí, keď prvú rovnicu vynásobíme číslom
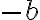 a druhú rovnicu číslom
a druhú rovnicu číslom
 . Po ich sčítaní dostaneme ...
. Po ich sčítaní dostaneme ...
Pre súčin komplexných čísel vyjadrených v goniometrickom tvare platí vlastnosť komutatívnosti a asociatívnosti. Dokážte to použitím Moivrovej vety.
Nech
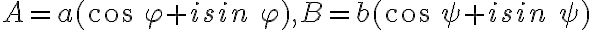 sú dve komplexné čísla vyjadrené v goniometrickom tvare a
sú dve komplexné čísla vyjadrené v goniometrickom tvare a 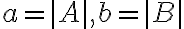 sú
absolútne hodnoty.
sú
absolútne hodnoty.
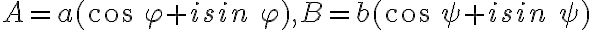 sú dve komplexné čísla vyjadrené v goniometrickom tvare a
sú dve komplexné čísla vyjadrené v goniometrickom tvare a 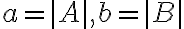 sú
absolútne hodnoty.
sú
absolútne hodnoty.
- Potom pre ich súčin platí
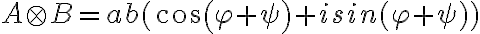 .
. - Vzhľadom na komutatívnosť sčítania v obore reálnych čísel, zrejme bude platiť
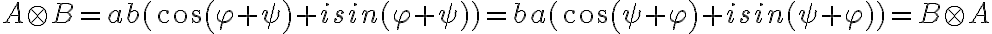 ,
,
čo je vlastnosť komutatívnosti súčinu komplexných čísel. - Podobne budeme postupovať pri asociatívnosti. Pri dokazovaní komutatívnosti a asociatívnosti sčítania komplexných čísel s výhodou použijeme algebraické tvary.
