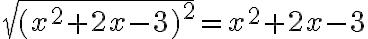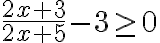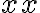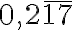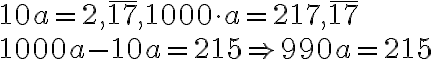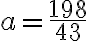Zavedenie číselných oborov N, Z, Q
Racionálne čísla
Riešenie - úloha 6 až 10
Riešenie.
Zrejme platí
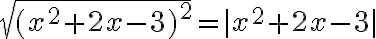
po dosadení dostávame rovnicu
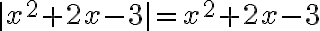 .
.
Kvadratická rovnica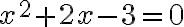 má reálne korene
má reálne korene
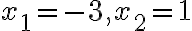 . Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
. Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
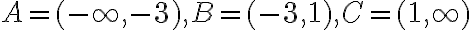 .
.
Zistíme, že riešením danej rovnice v intervaloch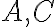 je ľubovoľné racionálne číslo a v intervale
je ľubovoľné racionálne číslo a v intervale
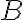 nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
Odpoveď. Riešením sú racionálne čísla množiny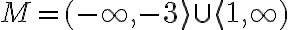 .
.
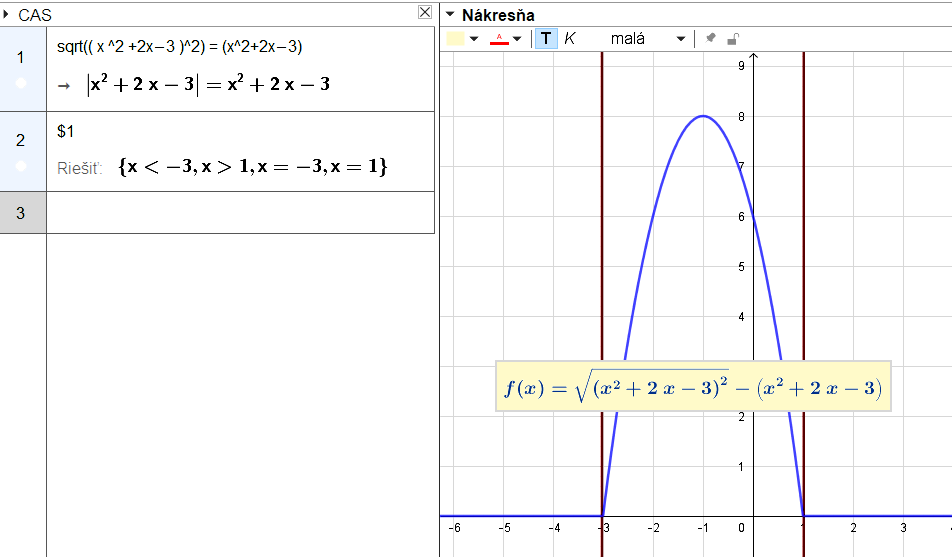
Grafické riešenie - GeoGebra, otvor applet Tu
Zrejme platí
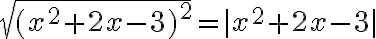
po dosadení dostávame rovnicu
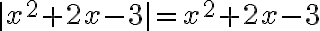 .
.
Kvadratická rovnica
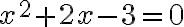 má reálne korene
má reálne korene
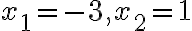 . Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
. Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
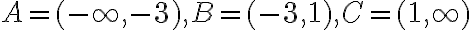 .
.
Zistíme, že riešením danej rovnice v intervaloch
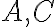 je ľubovoľné racionálne číslo a v intervale
je ľubovoľné racionálne číslo a v intervale
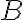 nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
Odpoveď. Riešením sú racionálne čísla množiny
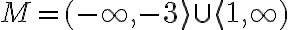 .
.
Grafické riešenie - GeoGebra, otvor applet Tu
U8: Do rovnostranného trojuholníka
 so stranou dĺžky a je vpísaný štvorec
so stranou dĺžky a je vpísaný štvorec
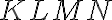 tak, že strana
tak, že strana
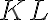 leží na úsečke
leží na úsečke
 . Úsečka
. Úsečka
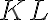 je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
 so stranou dĺžky a je vpísaný štvorec
so stranou dĺžky a je vpísaný štvorec
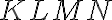 tak, že strana
tak, že strana
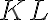 leží na úsečke
leží na úsečke
 . Úsečka
. Úsečka
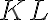 je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
Riešenie.
Výška rovnostranného trojuholníka je rovná
je rovná
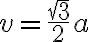
Veľkosť strany štvorca s určíme využitím podobnosti trojuholníkov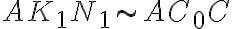 :[1]
:[1]
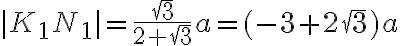 .
.
Pokračujeme určením veľkosti strán ďalších vpísaných štvorcov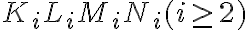 . Potom určíme pomer týchto strán.
. Potom určíme pomer týchto strán.
Dokážte, že v dvoch po sebe idúcich štvorcoch je pomer strán konštatný.
Tento pomer je koeficient geometrického radu, v ktorom pre prvý člen patí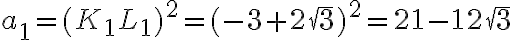 .
.
Výsledok je ...
Výška rovnostranného trojuholníka
 je rovná
je rovná
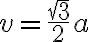
Veľkosť strany štvorca s určíme využitím podobnosti trojuholníkov
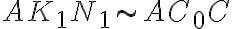 :[1]
:[1]
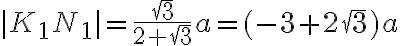 .
.
Pokračujeme určením veľkosti strán ďalších vpísaných štvorcov
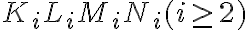 . Potom určíme pomer týchto strán.
. Potom určíme pomer týchto strán.
Dokážte, že v dvoch po sebe idúcich štvorcoch je pomer strán konštatný.
Tento pomer je koeficient geometrického radu, v ktorom pre prvý člen patí
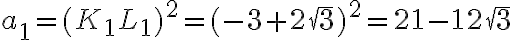 .
.
Výsledok je ...
Pozrite si riešenie od profesora Bukovského[2] Tu.
[1] Bača, M. a kol.: Zbierka riešených a neriešených úloh z matematiky. TU v Košiciach, 2011. Dostupné Tu
[2] Bukovský, L.: Úvod do matematiky. UPJŠ Košice. 2001. Dostupné Tu