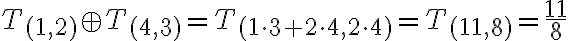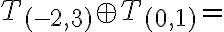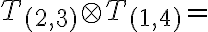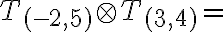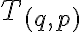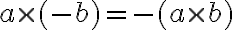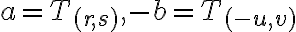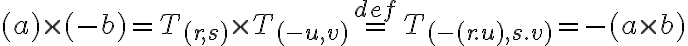Zavedenie číselných oborov N, Z, Q
Racionálne čísla
Riešenie - úloha 1 až 5
U2 a U3
-
Ukážte, že pre ľubovoľné racionálne číslo
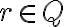 rôzne od nuly existuje racionálne číslo
rôzne od nuly existuje racionálne číslo
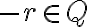 , pre ktoré platí
, pre ktoré platí
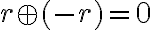 .
. - ukážte, že racionálne číslo
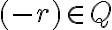 reprezentuje trieda rozkladu
reprezentuje trieda rozkladu
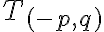 , ak racionálne číslo
, ak racionálne číslo
 reprezentuje trieda
reprezentuje trieda
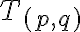 ,
,
- dokážte, že pre ľubovoľné racionálne čísla
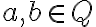 platí:
platí:
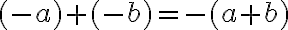 .
.
-
Ukážte, že pre ľubovoľné racionálne číslo
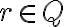 rôzne od nuly existuje racionálne číslo
rôzne od nuly existuje racionálne číslo
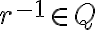 , pre ktoré platí
, pre ktoré platí
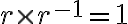 .
.
U2 a U3: Riešenie.
- Pre racionálne číslo
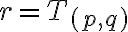 rôzne od nuly
rôzne od nuly
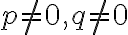 platí
platí 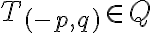 . Označme
. Označme
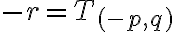 a počítajme
a počítajme
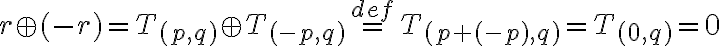
- Nech
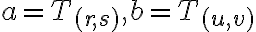 sú racionálne čísla, potom pre súčet racionálnych čísel
sú racionálne čísla, potom pre súčet racionálnych čísel
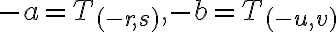 dostaneme
dostaneme
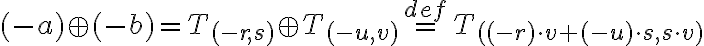
operácie sčítania a násobenia v oboroch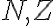 sú komutatívne, asociatívne a disributívne, preto
sú komutatívne, asociatívne a disributívne, preto
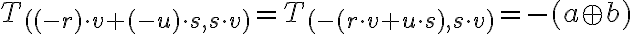
- Zrejme existuje racionálne číslo
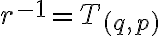 , ktoré spĺňa podmienku
, ktoré spĺňa podmienku
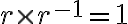 . Počítajme
. Počítajme
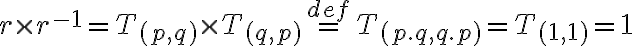 .
Pozrite si model násobenia zlomkov Tu
.
Pozrite si model násobenia zlomkov Tu
Riešenie.
Nech
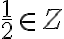 ,
,
potom existujú prirodzené čísla
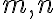 a zároveň platí
a zároveň platí
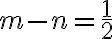 .
.
Po úprave dostaneme
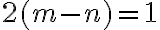 .
.
Na ľavej strane je párne číslo a na pravej nepárne, čo nie je možné. Tým je dôkaz ukončený.
Nech
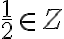 ,
,
potom existujú prirodzené čísla
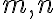 a zároveň platí
a zároveň platí
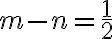 .
.
Po úprave dostaneme
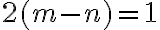 .
.
Na ľavej strane je párne číslo a na pravej nepárne, čo nie je možné. Tým je dôkaz ukončený.
U5: Pomocou tried rozkladu dokážte, že pre ľubovoľné racionálne čísla
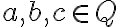 platí komutatívny a asociatívny zákon pre sčítanie.
platí komutatívny a asociatívny zákon pre sčítanie.
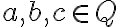 platí komutatívny a asociatívny zákon pre sčítanie.
platí komutatívny a asociatívny zákon pre sčítanie.
Riešenie.
- Dokážeme platnosť komutatívneho zákona. Z definície súčtu dvoch tried
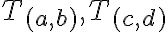 v tomto poradí dostávame
v tomto poradí dostávame
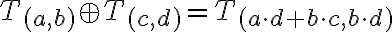
a pre súčet v opačnom poradí dostávame
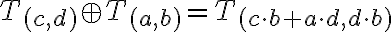
Keďže komutatívny zákon platí pre súčet aj súčin v obore celých čísel, tak zrejme platí aj rovnosť
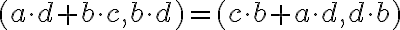 .
.
Odkiaľ vyplýva, že pravá strana vo vzťahu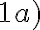 je rovná pravej strane vo vzťahu
je rovná pravej strane vo vzťahu
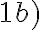 . Preto platí komutatívny zákon pre sčítanie.
. Preto platí komutatívny zákon pre sčítanie. - Dokážeme platnosť asociatívneho zákona. Nech triedy
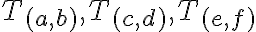 reprezentujú tri racionálne čísla, potom z definície súčtu dostávame
reprezentujú tri racionálne čísla, potom z definície súčtu dostávame
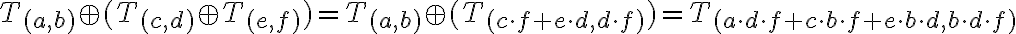
Analogickými úvahami ako v prípade ukážeme, že
ukážeme, že
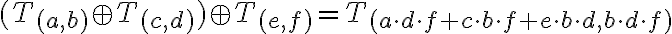
Odkiaľ vyplýva, že pravá strana vo vzťahu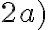 je rovná pravej strane vo vzťahu
je rovná pravej strane vo vzťahu
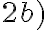 . Preto platí asociatívny zákon.
Tým je dôkaz ukončený.
. Preto platí asociatívny zákon.
Tým je dôkaz ukončený.
- Podobne môžeme postupovať pri dôkaze komutatívnosti a asociatívnosti násobenia racionálnych čísel (DÚ).