Obraz kružnice v kolineácii, kužeľosečky.
Obraz kružnice
Kružnica → elipsa
Tvrdenie
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka: elipsa, parabola alebo hyperbola.
Toto tvrdenie sa ľahko dokáže pomocou metód analytickej geometrie.
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka: elipsa, parabola alebo hyperbola.
Toto tvrdenie sa ľahko dokáže pomocou metód analytickej geometrie.
Poznámky.
Regulárne kužeľosečky môžeme klasifikovať podľa toho, koľko majú nevlastných bodov.
Regulárne kužeľosečky môžeme klasifikovať podľa toho, koľko majú nevlastných bodov.
- Elipsa má všetky body vlastné. Teda nemá nevlastné body.
 Kružnica s úbežnicou
Kružnica s úbežnicou  nemá spoločný bod.
nemá spoločný bod. - Parabola má jeden nevlastný bod (má jednu vetvu).
 Kružnica s úbežnicou
Kružnica s úbežnicou  má spoločný jeden bod.
má spoločný jeden bod. - Hyperbola má dva nevlastní body (dve vetvy), ktoré leží v smere asymptóta.
 Kružnica s úbežnicou
Kružnica s úbežnicou  má dva spoločné body.
má dva spoločné body.
Cvičenie.
Zostrojte obraz kružnice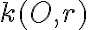 v stredovej kolineácii
v stredovej kolineácii
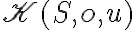 , ak kružnica
, ak kružnica  nemá s úbežnicou
nemá s úbežnicou  spoločný bod:
spoločný bod: 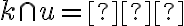 . Otvorte si zadanie Tu.
. Otvorte si zadanie Tu.
Riešenie
Keďže kružnica nemá s úbežnicou
nemá s úbežnicou  spoločný bod, tak obrazom bude elipsa.
spoločný bod, tak obrazom bude elipsa.
Celú konštrukciu si môžete stiahnuť Tu
Zostrojte obraz kružnice
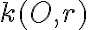 v stredovej kolineácii
v stredovej kolineácii
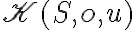 , ak kružnica
, ak kružnica  nemá s úbežnicou
nemá s úbežnicou  spoločný bod:
spoločný bod: 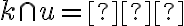 . Otvorte si zadanie Tu.
. Otvorte si zadanie Tu.Riešenie
Keďže kružnica
 nemá s úbežnicou
nemá s úbežnicou  spoločný bod, tak obrazom bude elipsa.
spoločný bod, tak obrazom bude elipsa.
- Na jej zostrojenie nám stačí, ak poznáme jej združene priemery1)
![[T_1R_1], [T_2R_2] [T_1R_1], [T_2R_2]](https://lms.umb.sk/filter/tex/pix.php/43d153c4fefd6ad3d9ff64df66940ab6.png) .
. - Zvoľme si ľubovoľný úbežník
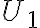 a zostrojme z neho dotyčnice
a zostrojme z neho dotyčnice
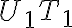 ,
,
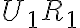 ku kružnici.
ku kružnici. - Zostrojme priesečník/úbežník
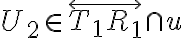 a opäť dotyčnice
a opäť dotyčnice
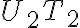 ,
,
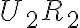 ku kružnici
ku kružnici - Úbežníky
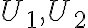 sa zobrazujú do nevlastných bodov, preto obrazy dotyčníc
sa zobrazujú do nevlastných bodov, preto obrazy dotyčníc
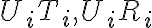 (
(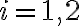 ) budú rovnobežné priamky.
) budú rovnobežné priamky.
Celú konštrukciu si môžete stiahnuť Tu
Z postupu riešenia vyplýva, že tetiva kružnice, ktorá spája dotykové body je priemerom elipsy. Na zostrojenie hlavnej a vedľajšej osi elipsy môžeme použiť napr. Rytzovu konštrukciu.
1) Dva priemery elipsy sa nazývajú združené, ak sú dotyčnice v krajných bodoch jedného priemeru rovnobežné s druhým priemerom a naopak.
