Obraz kružnice v kolineácii, kužeľosečky.
Rozšírený Euklidovský priestor
Pri riešení niektorých geometrických úloh je výhodné rozšíriť Euklidovský priestor o tzv. nevlastné prvky. V rozšírenom Euklidovskom priestore pre vlastné útvary platia všetky vety a axiómy, ktoré sme uviedli v Hilbertovom axiomatickom systéme. Pre nevlastné prvky je potrebné doplniť o niektoré špecifické tvrdenia projektívnej geometrie.
Nevlastný bod
- Nech je daná priamka
 a bod
a bod 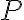 , ktorý na nej neleží.
, ktorý na nej neleží. - Postupne otáčame priamku
 okolo bodu
okolo bodu 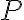 .
. - Zostrojme priesečníky
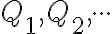 s priamkou
s priamkou  .
. - Pri vhodnom nastavení bude priamka
 rovnobežná s priamkou
rovnobežná s priamkou  (resp. splynie s priamkou
(resp. splynie s priamkou  ).
). - V tomto prípade v Euklidovskom priestore
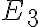 neexistuje priesečník.
neexistuje priesečník.
- Ako limitný prípad budeme rovnobežky považovať za priamky, ktoré majú spoločný bod v nekonečne.
- Tento bod, ktorý nevieme zobraziť v
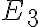 , nazveme nevlastný bod a označíme ho
, nazveme nevlastný bod a označíme ho
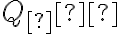 .
.
Nevlastná priamka
Analogickou úvahou/konštrukciou môžeme uvažovať o priesečnici dvoch rovnobežných rovín. Priesečnicu rovnobežných rovín nazveme nevlastná priamka roviny. Existuje len jedna nevlastná priamka roviny, ktorá zrejme obsahuje všetky nevlastné body tejto roviny.
Nevlastná rovina je množina všetkých nevlastných bodov a nevlastných priamok rozšíreného Euklidovského priestoru. Existuje len jedna. Každý priestor má práve jednu nevlastnú rovinu.
Analogickou úvahou/konštrukciou môžeme uvažovať o priesečnici dvoch rovnobežných rovín. Priesečnicu rovnobežných rovín nazveme nevlastná priamka roviny. Existuje len jedna nevlastná priamka roviny, ktorá zrejme obsahuje všetky nevlastné body tejto roviny.
Nevlastná rovina je množina všetkých nevlastných bodov a nevlastných priamok rozšíreného Euklidovského priestoru. Existuje len jedna. Každý priestor má práve jednu nevlastnú rovinu.
Poznámky.
- Zavedenie nevlastných prvkov vyšlo z pojmu rovnobežnosti priamok a rovín.
- Nevlastné prvky ale nemajú niektoré vlastnosti, ktoré majú vlastné prvky.
- Nie je možné napríklad hovoriť o smere nevlastnej priamky, veľkosti úsečky na nevlastnej priamke a i.
