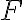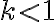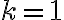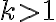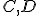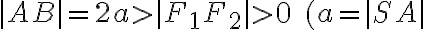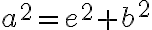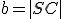Obraz kružnice v kolineácii, kužeľosečky.
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Obraz kružnice v kolineácii, kužeľosečky. |
| Vytlačil(a): | Guest user |
| Dátum: | streda, 3 júla 2024, 11:23 |
Rozšírený Euklidovský priestor
Pri riešení niektorých geometrických úloh je výhodné rozšíriť Euklidovský priestor o tzv. nevlastné prvky. V rozšírenom Euklidovskom priestore pre vlastné útvary platia všetky vety a axiómy, ktoré sme uviedli v Hilbertovom axiomatickom systéme. Pre nevlastné prvky je potrebné doplniť o niektoré špecifické tvrdenia projektívnej geometrie.
Nevlastný bod
- Nech je daná priamka
 a bod
a bod 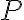 , ktorý na nej neleží.
, ktorý na nej neleží. - Postupne otáčame priamku
 okolo bodu
okolo bodu 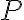 .
. - Zostrojme priesečníky
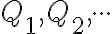 s priamkou
s priamkou  .
. - Pri vhodnom nastavení bude priamka
 rovnobežná s priamkou
rovnobežná s priamkou  (resp. splynie s priamkou
(resp. splynie s priamkou  ).
). - V tomto prípade v Euklidovskom priestore
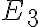 neexistuje priesečník.
neexistuje priesečník.
- Ako limitný prípad budeme rovnobežky považovať za priamky, ktoré majú spoločný bod v nekonečne.
- Tento bod, ktorý nevieme zobraziť v
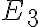 , nazveme nevlastný bod a označíme ho
, nazveme nevlastný bod a označíme ho
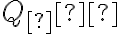 .
.
Nevlastná priamka
Analogickou úvahou/konštrukciou môžeme uvažovať o priesečnici dvoch rovnobežných rovín. Priesečnicu rovnobežných rovín nazveme nevlastná priamka roviny. Existuje len jedna nevlastná priamka roviny, ktorá zrejme obsahuje všetky nevlastné body tejto roviny.
Nevlastná rovina je množina všetkých nevlastných bodov a nevlastných priamok rozšíreného Euklidovského priestoru. Existuje len jedna. Každý priestor má práve jednu nevlastnú rovinu.
Analogickou úvahou/konštrukciou môžeme uvažovať o priesečnici dvoch rovnobežných rovín. Priesečnicu rovnobežných rovín nazveme nevlastná priamka roviny. Existuje len jedna nevlastná priamka roviny, ktorá zrejme obsahuje všetky nevlastné body tejto roviny.
Nevlastná rovina je množina všetkých nevlastných bodov a nevlastných priamok rozšíreného Euklidovského priestoru. Existuje len jedna. Každý priestor má práve jednu nevlastnú rovinu.
Poznámky.
- Zavedenie nevlastných prvkov vyšlo z pojmu rovnobežnosti priamok a rovín.
- Nevlastné prvky ale nemajú niektoré vlastnosti, ktoré majú vlastné prvky.
- Nie je možné napríklad hovoriť o smere nevlastnej priamky, veľkosti úsečky na nevlastnej priamke a i.
Obraz kružnice
Tvrdenie
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka: elipsa, parabola alebo hyperbola.
Toto tvrdenie sa ľahko dokáže pomocou metód analytickej geometrie alebo pomocou Quételet-Dandelin vety1).
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka: elipsa, parabola alebo hyperbola.
Toto tvrdenie sa ľahko dokáže pomocou metód analytickej geometrie alebo pomocou Quételet-Dandelin vety1).
Poznámky.
Regulárne kužeľosečky môžeme klasifikovať podľa toho, koľko majú nevlastných bodov.
Regulárne kužeľosečky môžeme klasifikovať podľa toho, koľko majú nevlastných bodov.
- Elipsa má všetky body vlastné. Teda nemá nevlastné body.
 Kružnica s úbežnicou
Kružnica s úbežnicou  nemá spoločný bod.
nemá spoločný bod. - Parabola má jeden nevlastný bod (má jednu vetvu).
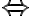 Kružnica s úbežnicou
Kružnica s úbežnicou  má spoločný jeden bod.
má spoločný jeden bod. - Hyperbola má dva nevlastní body (dve vetvy), ktoré leží v smere asymptóta.
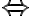 Kružnica s úbežnicou
Kružnica s úbežnicou  má dva spoločné body.
má dva spoločné body.
___________________________________________________________________________
1) Diplomová práca Kužeľosečky (Quetelet-Dandelin veta). Dostupné Tu.
1) Diplomová práca Kužeľosečky (Quetelet-Dandelin veta). Dostupné Tu.
Kružnica → elipsa
Tvrdenie
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka: elipsa, parabola alebo hyperbola.
Toto tvrdenie sa ľahko dokáže pomocou metód analytickej geometrie.
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka: elipsa, parabola alebo hyperbola.
Toto tvrdenie sa ľahko dokáže pomocou metód analytickej geometrie.
Poznámky.
Regulárne kužeľosečky môžeme klasifikovať podľa toho, koľko majú nevlastných bodov.
Regulárne kužeľosečky môžeme klasifikovať podľa toho, koľko majú nevlastných bodov.
- Elipsa má všetky body vlastné. Teda nemá nevlastné body.
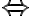 Kružnica s úbežnicou
Kružnica s úbežnicou  nemá spoločný bod.
nemá spoločný bod. - Parabola má jeden nevlastný bod (má jednu vetvu).
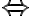 Kružnica s úbežnicou
Kružnica s úbežnicou  má spoločný jeden bod.
má spoločný jeden bod. - Hyperbola má dva nevlastní body (dve vetvy), ktoré leží v smere asymptóta.
 Kružnica s úbežnicou
Kružnica s úbežnicou  má dva spoločné body.
má dva spoločné body.
Cvičenie.
Zostrojte obraz kružnice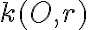 v stredovej kolineácii
v stredovej kolineácii
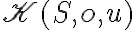 , ak kružnica
, ak kružnica  nemá s úbežnicou
nemá s úbežnicou  spoločný bod:
spoločný bod: 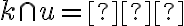 . Otvorte si zadanie Tu.
. Otvorte si zadanie Tu.
Riešenie
Keďže kružnica nemá s úbežnicou
nemá s úbežnicou  spoločný bod, tak obrazom bude elipsa.
spoločný bod, tak obrazom bude elipsa.
Celú konštrukciu si môžete stiahnuť Tu
Zostrojte obraz kružnice
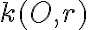 v stredovej kolineácii
v stredovej kolineácii
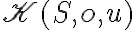 , ak kružnica
, ak kružnica  nemá s úbežnicou
nemá s úbežnicou  spoločný bod:
spoločný bod: 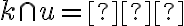 . Otvorte si zadanie Tu.
. Otvorte si zadanie Tu.Riešenie
Keďže kružnica
 nemá s úbežnicou
nemá s úbežnicou  spoločný bod, tak obrazom bude elipsa.
spoločný bod, tak obrazom bude elipsa.
- Na jej zostrojenie nám stačí, ak poznáme jej združene priemery1)
![[T_1R_1], [T_2R_2] [T_1R_1], [T_2R_2]](https://lms.umb.sk/filter/tex/pix.php/43d153c4fefd6ad3d9ff64df66940ab6.png) .
. - Zvoľme si ľubovoľný úbežník
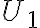 a zostrojme z neho dotyčnice
a zostrojme z neho dotyčnice
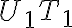 ,
,
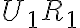 ku kružnici.
ku kružnici. - Zostrojme priesečník/úbežník
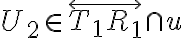 a opäť dotyčnice
a opäť dotyčnice
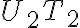 ,
,
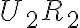 ku kružnici
ku kružnici - Úbežníky
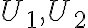 sa zobrazujú do nevlastných bodov, preto obrazy dotyčníc
sa zobrazujú do nevlastných bodov, preto obrazy dotyčníc
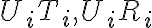 (
(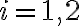 ) budú rovnobežné priamky.
) budú rovnobežné priamky.
Celú konštrukciu si môžete stiahnuť Tu
Z postupu riešenia vyplýva, že tetiva kružnice, ktorá spája dotykové body je priemerom elipsy. Na zostrojenie hlavnej a vedľajšej osi elipsy môžeme použiť napr. Rytzovu konštrukciu.
1) Dva priemery elipsy sa nazývajú združené, ak sú dotyčnice v krajných bodoch jedného priemeru rovnobežné s druhým priemerom a naopak.
Kružnica → parabola
Cvičenie.
Zostrojte obraz kružnice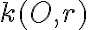 v stredovej kolineácii
v stredovej kolineácii
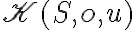 , ak kružnica
, ak kružnica  má s úbežnicou
má s úbežnicou  jeden spoločný bod:
jeden spoločný bod: 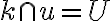 a os kolineácie pretína v dvoch bodoch
a os kolineácie pretína v dvoch bodoch
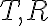 .
.
Riešenie
Keďže kružnica má s úbežnicou
má s úbežnicou  spoločný práve jeden bod, tak obrazom bude parabola.
spoločný práve jeden bod, tak obrazom bude parabola.
Zostrojte obraz kružnice
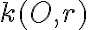 v stredovej kolineácii
v stredovej kolineácii
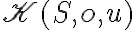 , ak kružnica
, ak kružnica  má s úbežnicou
má s úbežnicou  jeden spoločný bod:
jeden spoločný bod: 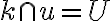 a os kolineácie pretína v dvoch bodoch
a os kolineácie pretína v dvoch bodoch
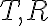 .
.
Riešenie
Keďže kružnica
 má s úbežnicou
má s úbežnicou  spoločný práve jeden bod, tak obrazom bude parabola.
spoločný práve jeden bod, tak obrazom bude parabola.
- Na jej zostrojenie nám stačí, ak poznáme jej dve dotyčnice
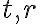 s dotykovými bodmi
s dotykovými bodmi
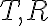 .
. - Pri použití lichobežníkovej metódy nám stačí zostrojiť obrazy dotyčníc
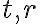 .
. - Zostrojme priesečník/úbežník
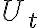 a smer
a smer
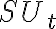 .
. - Obrazom dotyčnice
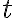 bude priamka prechádzajúca samodružným bodom
bude priamka prechádzajúca samodružným bodom
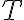 , ktorá je rovnobežná so smerom
, ktorá je rovnobežná so smerom
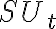 .
.
Poznámka.
V našej konštrukcii sme použili na "vykreslenie" paraboly nástroj "Množina bodov".
Veta
Spojnica priesečníka dvoch rôznych dotyčníc paraboly so stredom tetivy určenej ich dotykovými bodmi je rovnobežná s osou paraboly.
Spojnica priesečníka dvoch rôznych dotyčníc paraboly so stredom tetivy určenej ich dotykovými bodmi je rovnobežná s osou paraboly.
- Veďme bodom
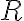 kolmicu
kolmicu
 k smeru osi paraboly. Smer osi paraboly zostrojíme podľa predchádzajúcej vety.
k smeru osi paraboly. Smer osi paraboly zostrojíme podľa predchádzajúcej vety. - Bodmi
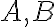 veďme rovnobežky s osou, ich priesečníky s kolmicou k označme
veďme rovnobežky s osou, ich priesečníky s kolmicou k označme
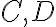 .
. - Vrchol
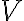 paraboly zostrojíme ako priesečník priamok
paraboly zostrojíme ako priesečník priamok
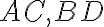 .
. - Os paraboly prechádza vrcholom a je rovnobežná s
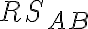 .
.
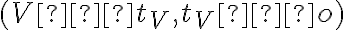 , na ktorej ležia päty všetkých kolmíc spustených z ohniska na dotyčnice paraboly.
Body
, na ktorej ležia päty všetkých kolmíc spustených z ohniska na dotyčnice paraboly.
Body
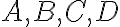 (nie nutne v tomto poradí) sú vrcholy lichobežníka (ak nie je spojnica
(nie nutne v tomto poradí) sú vrcholy lichobežníka (ak nie je spojnica
 kolmá na os paraboly), podľa ktorého dostala táto konštrukcia svoj názov.
kolmá na os paraboly), podľa ktorého dostala táto konštrukcia svoj názov.
1) Konštrukcia paraboly lichobežníkovou metódou, ak poznáme dve dotyčnice s dotykovými bodmi. Dostupné
Tu.
Kružnica → hyperbola
Cvičenie.
Zostrojte obraz kružnice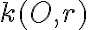 v stredovej kolineácii
v stredovej kolineácii
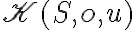 , ak kružnica
, ak kružnica  má s úbežnicou
má s úbežnicou  dva spoločné body:
dva spoločné body: 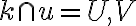 a os kolineácie pretína v dvoch bodoch
a os kolineácie pretína v dvoch bodoch
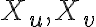 .
.
Riešenie
Keďže kružnica má s úbežnicou
má s úbežnicou  spoločné dva body, tak obrazom bude hyperbola.
spoločné dva body, tak obrazom bude hyperbola.
Zostrojte obraz kružnice
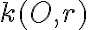 v stredovej kolineácii
v stredovej kolineácii
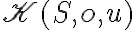 , ak kružnica
, ak kružnica  má s úbežnicou
má s úbežnicou  dva spoločné body:
dva spoločné body: 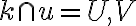 a os kolineácie pretína v dvoch bodoch
a os kolineácie pretína v dvoch bodoch
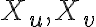 .
.
Riešenie
Keďže kružnica
 má s úbežnicou
má s úbežnicou  spoločné dva body, tak obrazom bude hyperbola.
spoločné dva body, tak obrazom bude hyperbola.
- Na jej zostrojenie nám stačí, ak poznáme jej asymptoty a jej hlavné vrcholy.
- Zostrojme dotyčnice
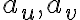 v bodoch
v bodoch
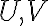 ku kružnici
ku kružnici  .
. - Nájdime obrazy
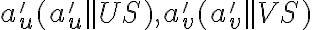 . Priamky
. Priamky 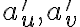 sú asymptoty hyperboly.
sú asymptoty hyperboly. - Priesečník asymptot
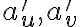 (ozn.
(ozn. 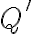 ) je stredom hyperboly.
) je stredom hyperboly. - Osy hyperboly
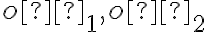 rozpoľujú uhly asymptot. Hlavnú os
rozpoľujú uhly asymptot. Hlavnú os 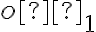 označíme tú,
pre ktorú odpovedajúca priamka
označíme tú,
pre ktorú odpovedajúca priamka 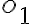 pretína kružnicu
pretína kružnicu  v dvoch bodoch. Označme ich
v dvoch bodoch. Označme ich
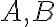 .
. - Bodom
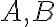 odpovedajú body
odpovedajú body
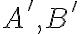 hyperboly
hyperboly 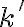 , ktoré sú jej hlavné vrcholy.
, ktoré sú jej hlavné vrcholy.
Poznámka.
V našej konštrukcii sme použili na "vykreslenie" hyperboly nástroj "Množina bodov".
Obraz ako GMB
Cvičenie.
Zostrojte obraz kružnice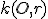 v stredovej kolineácii
v stredovej kolineácii 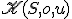 , ak kružnica
, ak kružnica  je v ľubovoľnej polohe k úbežnici
je v ľubovoľnej polohe k úbežnici  .
Otvorte si zadanie Tu.
.
Otvorte si zadanie Tu.
Riešenie
Pri riešení využijeme GeoGebra nástroj "Množina bodov". Pri jeho použití nám bude postačovať obraz jediného avšak ľubovoľného bodu križnice.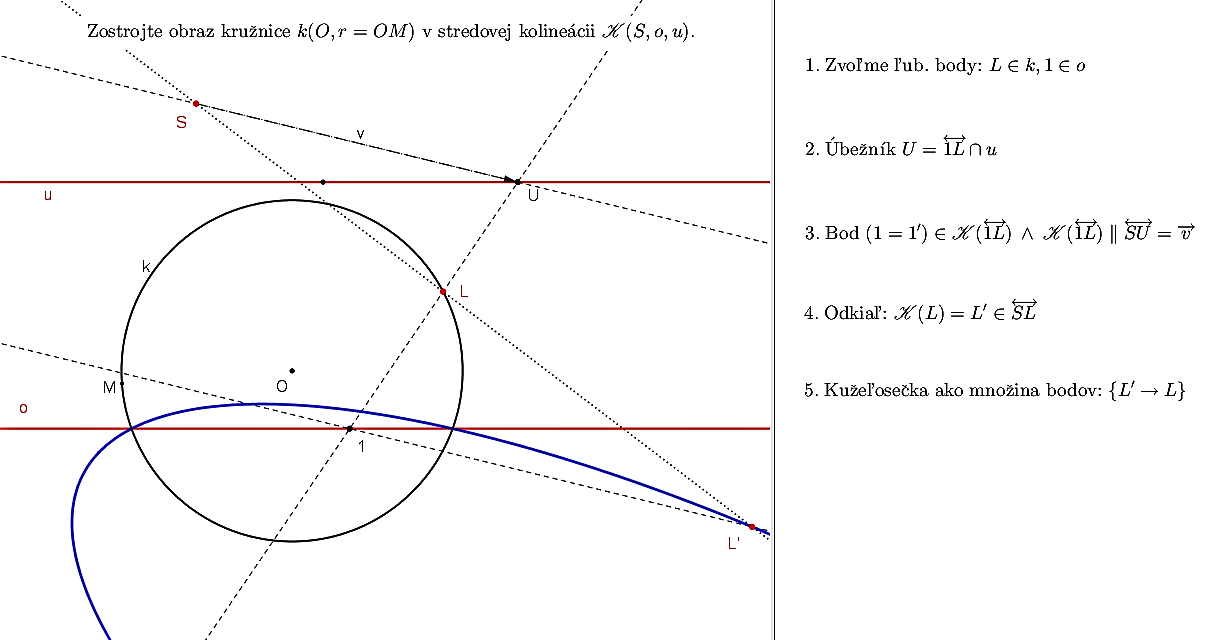
Celú konštrukciu si môžete stiahnuť Tu. Kolineácia v základnej polohe Tu.
Zostrojte obraz kružnice
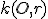 v stredovej kolineácii
v stredovej kolineácii 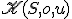 , ak kružnica
, ak kružnica  je v ľubovoľnej polohe k úbežnici
je v ľubovoľnej polohe k úbežnici  .
Otvorte si zadanie Tu.
.
Otvorte si zadanie Tu.
Riešenie
Pri riešení využijeme GeoGebra nástroj "Množina bodov". Pri jeho použití nám bude postačovať obraz jediného avšak ľubovoľného bodu križnice.
- Zvolíme si ľubovoľný bod
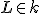 .
. - Zostrojíme obraz tohto bodu
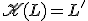 .
. - Aktivujeme nástroj "Množina bodov", potom ukážeme na bod
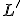 a následne na bod
a následne na bod 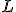 .
. - GeoGebra vykreslí odpovedajúcu kužeľosečku.

Celú konštrukciu si môžete stiahnuť Tu. Kolineácia v základnej polohe Tu.
...
Kuželosečky
Kužeľosečky sú krivky, ktoré, ako nám napovedá ich názov, je možné vytvoriť ako rezy rotačnej kužeľovej plochy rovinou. S takýmito krivkami sa stretávame v bežnom živote.
- Predstavte si napríklad hranicu hladiny vody v naklonenom pohári, kde hladina vody predstavuje rovinu rezu.
- Pri osvetlení baterkou na stenu a pozorujeme, ako sa osvetlená plocha mení v závislosti na polohe osi baterky vzhľadom na rovinu steny. Ak je os baterky v polohe kolmej k rovine múru, bude hranicu osvetlenej časti tvoriť kružnica, pri naklonení dostávame elipsu, alebo v určitej polohe dostaneme parabolu a ak nakloníme baterku ešte viac bude hranicou osvetlenej časti hyperbola.1)
Rezy rovinou na kužeľovej ploche, ktorá vznikne rotáciou dvoch rôznobežných priamok okolo osi ich uhla.
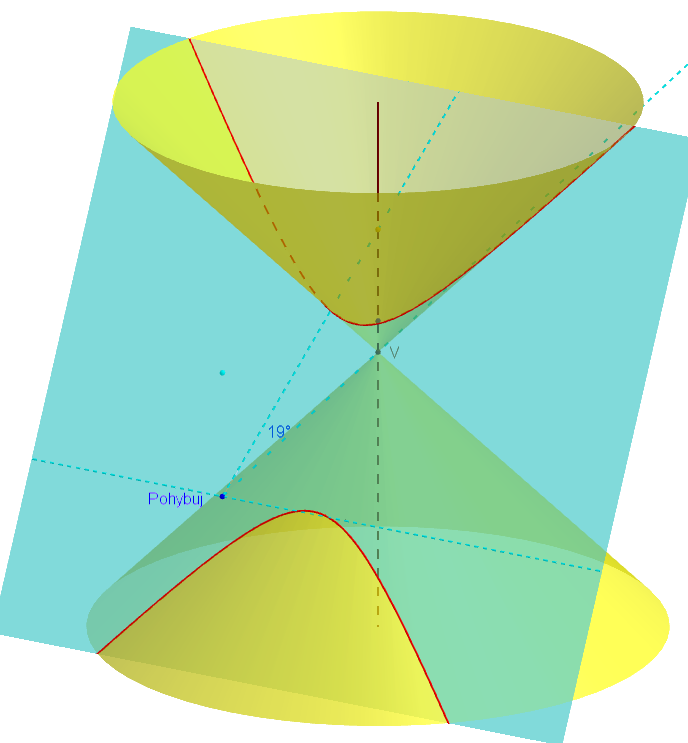 Otvorte si applet Tu
Otvorte si applet Tu
___________________________________________________________________________
1) Obrázky sú prevzaté s práce "Deskriptivní geometrie na MFF UK"
1) Obrázky sú prevzaté s práce "Deskriptivní geometrie na MFF UK"
Definícia kužeľosečky
Všeobecná definícia kuželosečky
Kužeľosečka je množina všetkých bodov v rovine, ktoré majú od pevného bodu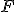 a pevne zvolenej priamky
a pevne zvolenej priamky 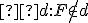 stály pomer vzdialeností rovný konštante
stály pomer vzdialeností rovný konštante  . Pre
. Pre
Kužeľosečka je množina všetkých bodov v rovine, ktoré majú od pevného bodu
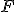 a pevne zvolenej priamky
a pevne zvolenej priamky 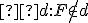 stály pomer vzdialeností rovný konštante
stály pomer vzdialeností rovný konštante  . Pre
. Pre
Bod 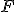 sa nazýva ohnisko kužeľosečky, priamka
sa nazýva ohnisko kužeľosečky, priamka 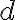 riadiaca priamka (direktrix). Číslo
riadiaca priamka (direktrix). Číslo  sa nazýva numerická výstrednosť.
sa nazýva numerická výstrednosť.
Týmto spôsobom môžeme definovať všetky regulárne kužeľosečky okrem kružnice.
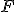 sa nazýva ohnisko kužeľosečky, priamka
sa nazýva ohnisko kužeľosečky, priamka 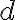 riadiaca priamka (direktrix). Číslo
riadiaca priamka (direktrix). Číslo  sa nazýva numerická výstrednosť.
sa nazýva numerická výstrednosť.
Týmto spôsobom môžeme definovať všetky regulárne kužeľosečky okrem kružnice.
Poznámky
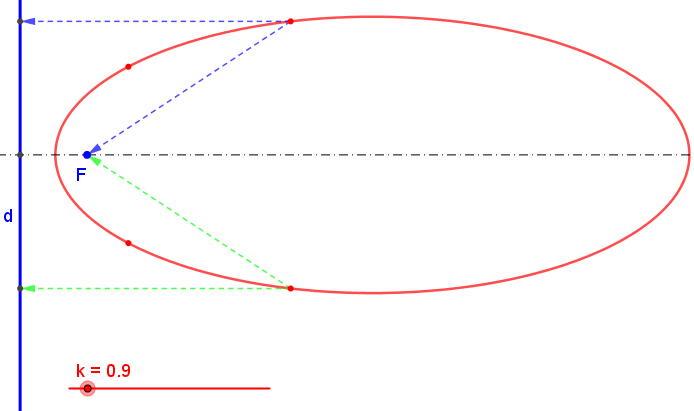
Na demonštráciu konštrukcie kužeľosečiek je možné s výhodou využiť sieť kružníc a priamok. Ak zvolíme ohnisko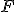 v strede sústavy kružníc a riadiacu priamku sťažíme s ľubovoľnou priamkou (tak, aby
v strede sústavy kružníc a riadiacu priamku sťažíme s ľubovoľnou priamkou (tak, aby 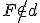 ), môžeme jednotlivé body kuželosečiek
hľadať ako priesečníky kružníc a priamok ktorých polomer a vzdialenosť od riadiacej priamky sú v konštantnom pomere.
), môžeme jednotlivé body kuželosečiek
hľadať ako priesečníky kružníc a priamok ktorých polomer a vzdialenosť od riadiacej priamky sú v konštantnom pomere.
 Otvorte si applet
Tu
Otvorte si applet
Tu
Na demonštráciu konštrukcie kužeľosečiek je možné s výhodou využiť sieť kružníc a priamok. Ak zvolíme ohnisko
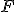 v strede sústavy kružníc a riadiacu priamku sťažíme s ľubovoľnou priamkou (tak, aby
v strede sústavy kružníc a riadiacu priamku sťažíme s ľubovoľnou priamkou (tak, aby 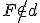 ), môžeme jednotlivé body kuželosečiek
hľadať ako priesečníky kružníc a priamok ktorých polomer a vzdialenosť od riadiacej priamky sú v konštantnom pomere.
), môžeme jednotlivé body kuželosečiek
hľadať ako priesečníky kružníc a priamok ktorých polomer a vzdialenosť od riadiacej priamky sú v konštantnom pomere.
Applet - Tlačidlá
Tu
Ohniskové vlastnosti
Bodová konštrukcia a ohniskové vlastnosti elipsy. Okrem všeobecnej definície kužeľosečky sa pre elipsu využíva definícia,
ktorá umožňuje jednoduchšiu bodovú konštrukciu elipsy.
Elipsa
je množina všetkých bodov v danej rovine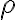 , ktorých súčet vzdialeností od dvoch rôznych pevných bodov
, ktorých súčet vzdialeností od dvoch rôznych pevných bodov 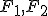 je rovný danému číslu
je rovný danému číslu 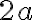 ,
ktoré je väčšie ako vzdialenosť bodov
,
ktoré je väčšie ako vzdialenosť bodov 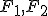 .
.
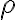 , ktorých súčet vzdialeností od dvoch rôznych pevných bodov
, ktorých súčet vzdialeností od dvoch rôznych pevných bodov 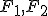 je rovný danému číslu
je rovný danému číslu 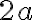 ,
ktoré je väčšie ako vzdialenosť bodov
,
ktoré je väčšie ako vzdialenosť bodov 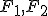 .
.
Všeobecné body elipsy
Pre bod M platí: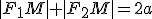 . Konštrukciu všeobecných bodov tak možno ľahko vykonať pomocou kružidla1).
. Konštrukciu všeobecných bodov tak možno ľahko vykonať pomocou kružidla1).
Pre bod M platí:
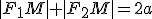 . Konštrukciu všeobecných bodov tak možno ľahko vykonať pomocou kružidla1).
. Konštrukciu všeobecných bodov tak možno ľahko vykonať pomocou kružidla1).
Poznámky.
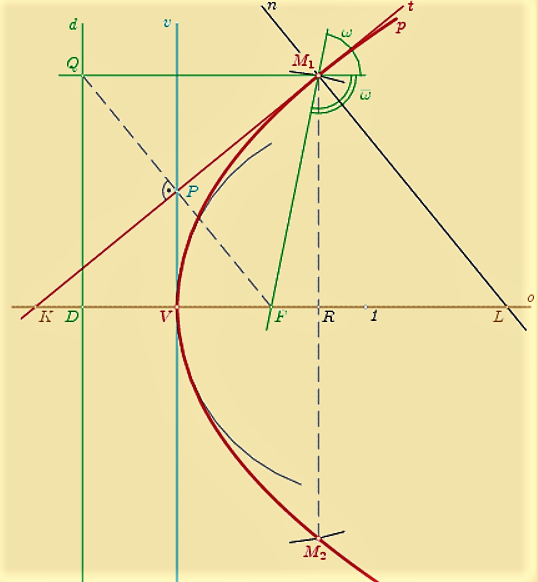
Parabola je množina všetkých bodov v danej rovine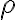 , ktoré majú rovnakú vzdialenosť od danej priamky
, ktoré majú rovnakú vzdialenosť od danej priamky 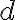 a od daného bodu
a od daného bodu 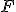 , ktorý na priamke
, ktorý na priamke 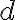 neleží.
neleží.
 Bodová konštrukcia
Tu
Bodová konštrukcia
Tu
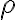 , ktoré majú rovnakú vzdialenosť od danej priamky
, ktoré majú rovnakú vzdialenosť od danej priamky 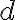 a od daného bodu
a od daného bodu 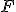 , ktorý na priamke
, ktorý na priamke 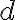 neleží.
neleží.
 Bodová konštrukcia
Tu
Bodová konštrukcia
Tu
Poznámky.
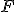 - ohnisko;
- ohnisko; 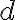 - riadiaca priamka;
- riadiaca priamka; 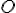 - os; vzdialenosť
- os; vzdialenosť 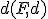 - parameter paraboly;
- parameter paraboly; 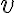 ... vrcholová dotyčnica;
... vrcholová dotyčnica; 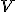 - vrchol (stred úsečky
- vrchol (stred úsečky 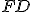 )
)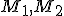 - všeobecné body paraboly priamka
- všeobecné body paraboly priamka 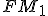 a rovnobežka s osou bodom
a rovnobežka s osou bodom 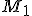 - sprievodič bodu
- sprievodič bodu 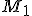 ;
uhol
;
uhol 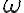 (a uhol k nemu vrcholový) je tzv. vonkajší uhol sprievodičov
(a uhol k nemu vrcholový) je tzv. vonkajší uhol sprievodičov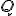 - bod súmerne združený s ohniskom
- bod súmerne združený s ohniskom 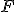 podľa dotyčnice
podľa dotyčnice 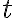 ; 1 ... stred hyperoskulačnej kružnice vo vrchole
; 1 ... stred hyperoskulačnej kružnice vo vrchole 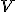 ;
platí
;
platí 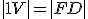
Hyperbola je množinou všetkých bodov v danej rovine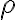 , pre ktoré je absolútna hodnota rozdielu vzdialeností od dvoch rôznych pevných bodov
, pre ktoré je absolútna hodnota rozdielu vzdialeností od dvoch rôznych pevných bodov 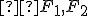 je rovný danému číslu
je rovný danému číslu 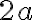 , ktoré je menšie ako vzdialenosť bodov
, ktoré je menšie ako vzdialenosť bodov 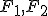 .
.
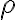 , pre ktoré je absolútna hodnota rozdielu vzdialeností od dvoch rôznych pevných bodov
, pre ktoré je absolútna hodnota rozdielu vzdialeností od dvoch rôznych pevných bodov 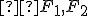 je rovný danému číslu
je rovný danému číslu 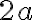 , ktoré je menšie ako vzdialenosť bodov
, ktoré je menšie ako vzdialenosť bodov 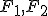 .
.
___________________________________________________________________________
1) Applety ku kužeľosečkám nájdete od autora Martina Vinklera Tu
1) Applety ku kužeľosečkám nájdete od autora Martina Vinklera Tu