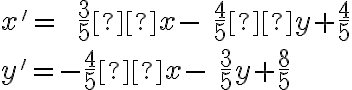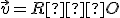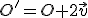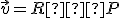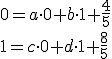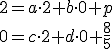Afinná geometria
Zhodnostné zobrazenia
Osová súmernosť
Zhodnostné zobrazenie v rovine Osová súmernosť - ukážka
Osová súmernosť určená troma bodmi.
- Na určenie transformačných rovníc osovej súmernosti určenej osou súmernosti
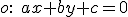 budeme potrebovať obrazy
troch rôznych bodov a ich obrazy v danej osovej súmernosti.
budeme potrebovať obrazy
troch rôznych bodov a ich obrazy v danej osovej súmernosti.
Najvýhodnejšie bude ak si zvolíme dva rôzne samodružné body a nejaký tretí bod tak, aby všetky tri boli nekolineárne. Takými bodmi pri takto danej osi súmernosti sú napríklad- dva body na osi súmernosti
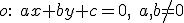 , pre ktoré platí
, pre ktoré platí ![\small A=[0,\frac{-c}{b}] \small A=[0,\frac{-c}{b}]](https://lms.umb.sk/filter/tex/pix.php/dd67a08dcc145362b583cb2c84e94ce1.png) a
a ![\small B=[\frac{-c}{a},0] \small B=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/b35dafcb91a2f8e7f3b1e89aeb667a55.png) ,
prípad ak jeden z koeficientov
,
prípad ak jeden z koeficientov 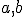 je rovný nule sa rieši zvlášť;
je rovný nule sa rieši zvlášť; - a tretí bod nech je počiatok súradnej sústavy
![\small O=[0,0] \small O=[0,0]](https://lms.umb.sk/filter/tex/pix.php/b84d8e89cd0f49322ca9230458995576.png) . Súradnice
. Súradnice 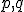 jeho obrazu
jeho obrazu ![\small O'=[p,q] \small O'=[p,q]](https://lms.umb.sk/filter/tex/pix.php/7843bc3154f974357ba963a4d076a5bc.png) určíme napríklad pomocou "Matrix calculator":
určíme napríklad pomocou "Matrix calculator":
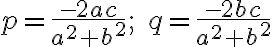 .
.
- dva body na osi súmernosti
- Potom dosadíme súradnice obrazov
![\small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0] \small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/15877e5bc55d5ebc24734962c92c4b49.png) do vzťahov
do vzťahov
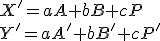
pričom musí platiť
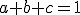 .
.
Dostaneme sústavu troch rovníc a využitím Matrix calculator dostaneme riešenie
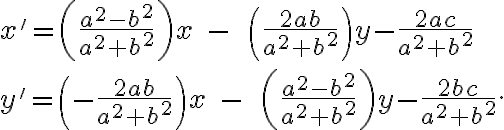
Osová súmernosť určená repérom.
Pri určovaní transformačných rovníc osovej súmernosti určenej osou súmernosti 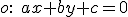 môžeme s výhodou použiť obraz súradného repéra
môžeme s výhodou použiť obraz súradného repéra
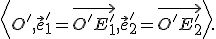
Postupne nájdeme:
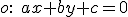 môžeme s výhodou použiť obraz súradného repéra
môžeme s výhodou použiť obraz súradného repéra
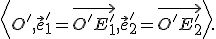
Postupne nájdeme:
- Obraz počiatku súradnej sústavy
![\small O'=[p,q] \small O'=[p,q]](https://lms.umb.sk/filter/tex/pix.php/9b214e8052bd6e14c00d9869d21efbbe.png) , ktorý určíme ako bod súmerný k bodu
, ktorý určíme ako bod súmerný k bodu ![\small O=[0,0] \small O=[0,0]](https://lms.umb.sk/filter/tex/pix.php/8b8044e750d6bcc556aaf5ed8f4fce4a.png) . Ten určíme pomocou priesečníka
. Ten určíme pomocou priesečníka 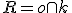 priamky
priamky 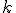 kolmej na priamku
kolmej na priamku  , ktorá prechádza bodom
, ktorá prechádza bodom 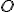 . Najskôr určíme
. Najskôr určíme
- Na určenie transformačných rovníc potrebujeme ešte aspoň dva rôzne body a ich obrazy v danej osovej súmernosti. Najvýhodnejšie bude ak si zvolíme dva samodružné body.
Takými bodmi sú ľubovoľné dva body na osi súmernosti
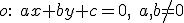 .
. - Zvoľme si
![\small A=[0,\frac{-c}{b}] \small A=[0,\frac{-c}{b}]](https://lms.umb.sk/filter/tex/pix.php/dd67a08dcc145362b583cb2c84e94ce1.png) a
a ![\small B=[\frac{-c}{a},0] \small B=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/b35dafcb91a2f8e7f3b1e89aeb667a55.png) , prípad ak jeden z koeficientov
, prípad ak jeden z koeficientov 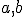 je rovný nule sa rieši zvlášť.
je rovný nule sa rieši zvlášť. - Potom dosadíme súradnice obrazov
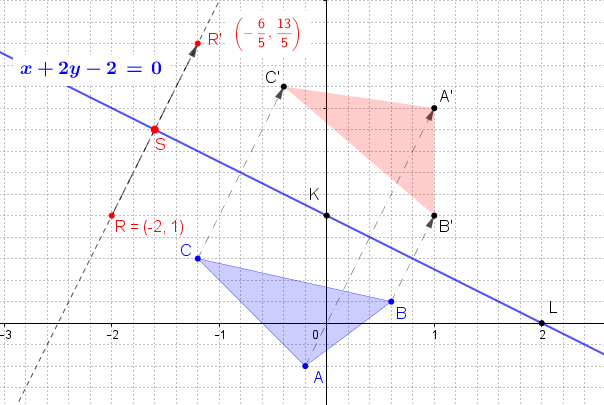
![\small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0] \small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/15877e5bc55d5ebc24734962c92c4b49.png) do vzťahu
do vzťahu
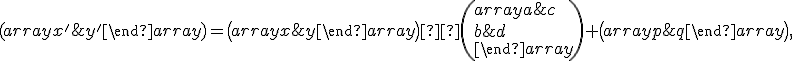 (1)
(1)
a dostaneme 4 rovnice o 4 neznámych
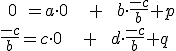
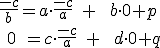
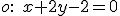
![\small O'=[\frac{4}{5},\frac{8}{5}],A'=[0,1],B'=[2,0] \small O'=[\frac{4}{5},\frac{8}{5}],A'=[0,1],B'=[2,0]](https://lms.umb.sk/filter/tex/pix.php/47a5a636b0a629e5cbc960ea12a787c6.png)