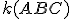Vybrané úlohy z matematickej olympiády
Množiny bodov danej vlastnosti.
- Daná je kružnica
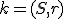 a vnútri nej bod
a vnútri nej bod 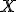 .
. - Určte množinu stredov všetkých tetív kružnice
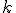 , ktoré prechádzajú bodom
, ktoré prechádzajú bodom 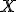 . Návod
Tu.
. Návod
Tu. - Určte množinu bodov, ktoré sú stredom nejakej jej tetivy, ktorá neobsahuje bod
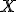 .
. - V rovine je daný ostrouhlý trojuholník
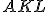 . Uvažujme ľubovoľný pravouholník
. Uvažujme ľubovoľný pravouholník 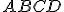 , ktorý je trojuholníku
, ktorý je trojuholníku 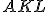 opísaný tak,
že bod
opísaný tak,
že bod 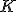 leží na strane
leží na strane 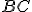 a bod
a bod 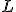 leží na strane
leží na strane 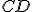 . Určte množinu priesečníkov
. Určte množinu priesečníkov  uhlopriečok
uhlopriečok 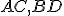 všetkých takých pravouholníkov
všetkých takých pravouholníkov 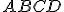 .
(Kat. A; 2004/2005; celoštátne kolo; úloha 4A - III - 4, znenie
Tu.) Applet s riešením
Tu.
.
(Kat. A; 2004/2005; celoštátne kolo; úloha 4A - III - 4, znenie
Tu.) Applet s riešením
Tu. - V rovine je daný rovnoramenný trojuholník
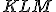 so základňou
so základňou 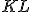 . Uvažujme ľubovoľné dve kružnice
. Uvažujme ľubovoľné dve kružnice 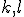 , ktoré majú
vonkajší dotyk a ktoré sa dotýkajú priamok
, ktoré majú
vonkajší dotyk a ktoré sa dotýkajú priamok 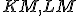 postupne v bodoch
postupne v bodoch 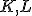 . Určte množinu dotykových bodov
. Určte množinu dotykových bodov 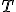 všetkých
takých kružníc
všetkých
takých kružníc 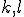 . (Kat. A; 2004/2005; celoštátne kolo; úloha 4)
Tu.
. (Kat. A; 2004/2005; celoštátne kolo; úloha 4)
Tu. - V rovine sú dané dve kružnice
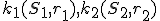 , pričom
, pričom  . Nájdite množinu všetkých bodov
. Nájdite množinu všetkých bodov 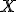 , ktoré neležia na priamke
, ktoré neležia na priamke 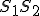 a
majú tú vlastnosť, že úsečky
a
majú tú vlastnosť, že úsečky 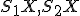 pretínajú postupne kružnice
pretínajú postupne kružnice 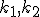 v bodoch, ktorých vzdialenosti od priamky
v bodoch, ktorých vzdialenosti od priamky 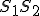 sa rovnajú.
(Kat. A; 2013/2014; krajské kolo; úloha 2, zadanie a riešenie Tu.) Applet s riešením Tu.
sa rovnajú.
(Kat. A; 2013/2014; krajské kolo; úloha 2, zadanie a riešenie Tu.) Applet s riešením Tu.
Rovnoľahlosť.
- Daná je úsečka
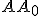 a priamka
a priamka  . Zostrojte trojuholník
. Zostrojte trojuholník 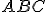 s vrcholom
s vrcholom 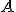 a výškou
a výškou
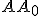 , ktorého ťažisko a stred kružnice opísanej ležia na priamke
, ktorého ťažisko a stred kružnice opísanej ležia na priamke  . Pozri 56. ročník MO, šk. rok 2006/2007, úloha B – I – 6. Riešenie - applet
Tu.
. Pozri 56. ročník MO, šk. rok 2006/2007, úloha B – I – 6. Riešenie - applet
Tu. - Označme
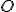 stred kružnice vpísanej pravouhlému trojuholníku
stred kružnice vpísanej pravouhlému trojuholníku 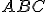 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole 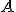 . Ďalej označme
. Ďalej označme 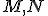 stredy úsečiek
stredy úsečiek 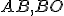 . Dokážte, že priamka
. Dokážte, že priamka 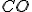 je dotyčnicou kružnice opísanej trojuholníku
je dotyčnicou kružnice opísanej trojuholníku 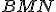 .
Kat. A; 2020/2021; celoštátne.; úloha 2. Riešenie - applet
Tu.
Návod Tu.
.
Kat. A; 2020/2021; celoštátne.; úloha 2. Riešenie - applet
Tu.
Návod Tu. - V rovine sú dané dva rôzne body
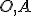 . Určte množinu ortocentier všetkých trojuholníkov
. Určte množinu ortocentier všetkých trojuholníkov 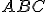 , pre ktoré je bod
, pre ktoré je bod 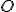 stredom kružnice opísanej.
Kat. A; 2019/2020; domáce kolo; úloha 2. Riešenie - applet
Tu.
stredom kružnice opísanej.
Kat. A; 2019/2020; domáce kolo; úloha 2. Riešenie - applet
Tu. - Dané sú dve rôznobežky
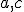 prechádzajúce bodom
prechádzajúce bodom 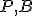 , ktorý na nich neleží. Zostrojte pravouholník
, ktorý na nich neleží. Zostrojte pravouholník 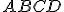 s
vrcholmi
s
vrcholmi 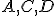 postupne na priamkach
postupne na priamkach 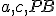 .
Kat. B; 2011/2012; domáce kolo; úloha 4. Riešenie - applet
Tu.
.
Kat. B; 2011/2012; domáce kolo; úloha 4. Riešenie - applet
Tu. - V rovine ω sú dané dva rôzne body
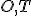 . Nájdite množinu vrcholov všetkých trojuholníkov, ktoré ležia v rovine
. Nájdite množinu vrcholov všetkých trojuholníkov, ktoré ležia v rovine 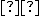 a majú ťažisko v
bode
a majú ťažisko v
bode 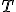 a stred opísanej kružnice v bode
a stred opísanej kružnice v bode 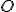 .
Kat. A; 2008/2009; celoštátne kolo; úloha 6. Riešenie - applet
Tu.
.
Kat. A; 2008/2009; celoštátne kolo; úloha 6. Riešenie - applet
Tu.
Rôzne úlohy.
Poznámky.
Posledná zmena: nedeľa, 22 októbra 2023, 16:06