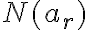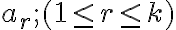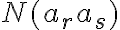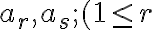Didaktika matematiky

Nech $M= \lbrace{x_1,x_2,..., x_n}\rbrace$ je množina objektov a $a_1,a_2, ... , a_k$ sú nejaké vlastnosti. Označme symbolom

• $N$ počet všetkých objektov, teda$N=n )$
• $N(a_r)$ počet všetkých objektov, ktoré majú vlastnosť $a_r; (1 \leq r \leq k )$
• $N(a_ra_s)$ počet tých objektov, ktoré majú súčasne vlastnosti $a_r,a_s; (1 \leq r$
• $N(a_ra_sa_t)$počet tých objektov, ktoré majú súčasne tri vlastnosti atď.
• Konečne, znakom $N(0)$ označme počet tých objektov, ktoré nemajú ani jednu z daných vlastností.

Príklad.
Písomnú prácu z matematiky písalo 35 študentov. Písomka obsahovala tri úlohy A, B, C. Vieme, že

1. Úlohu A vyriešilo 22 študentov, úlohu B vyriešilo 26 študentov, úlohu C vyriešilo 23 študentov.
2. Úlohu A aj úlohu B vyriešilo 16 študentov, úlohu A aj úlohu C vyriešilo 14 študentov, úlohu B aj úlohu C vyriešilo 17 študentov.
3. Všetky úlohy vyriešilo 10 študentov.
Zistite koľko študentov nevyriešilo ani jednu úlohu?

Riešenie.
Typické stredoškolské riešenie využíva grafickú schému - Vennov diagram, pomocou ktorého sa graficky vyjadruje príslušnosť prvkov k množine. V našom prípade to bude Vennov diagram pre tri množiny.

V diagrame postupne zapisujeme hodnoty

• 10
• 6 = 16 - 10,   4 = 14 - 10,   7 = 17 – 10
• 2 = 22 – (16 + 14) + 10,   3 = 26 – (16 + 17) + 10,   2 = 23 – (14 + 17) + 10
• 1 = 35 - (22 + 26 + 23) + (16 + 14 + 17) – 10 = 35 – 71 + 47
Všimnime si, že znamienka pri zátvorkách (vrátane posledného sčítanca sa striedajú. Môžeme ich určiť pomocou mocniny $\left(-1\right)^k; k=1,2,\ldots$.