Kombinatorika
Permutácie a variácie
Definícia.
Nech označujeme akúkoľvek
označujeme akúkoľvek  -prvkovú množinu. Permutáciou množiny
-prvkovú množinu. Permutáciou množiny
 nazývame jej bijektívne zobrazenie na seba.
nazývame jej bijektívne zobrazenie na seba.
Nech
 označujeme akúkoľvek
označujeme akúkoľvek  -prvkovú množinu. Permutáciou množiny
-prvkovú množinu. Permutáciou množiny
 nazývame jej bijektívne zobrazenie na seba.
nazývame jej bijektívne zobrazenie na seba.
Napríklad zobrazenie
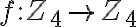 dané predpisom:
dané predpisom:
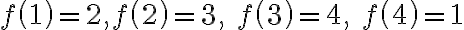
je bijekcia množiny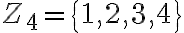 na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
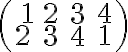
alebo jednoducho ako postupnosť
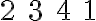 .
.
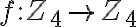 dané predpisom:
dané predpisom:
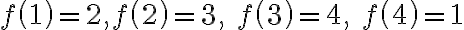
je bijekcia množiny
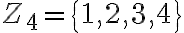 na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
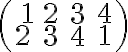
alebo jednoducho ako postupnosť
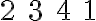 .
.
Príklad.
Nájdite všetky permutácie ľubovoľnej štvorprvkovej množiny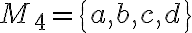 .
.
Riešenie.
Nech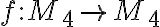 je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
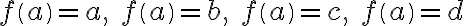 .
.
Ak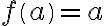 , tak obraz prvku
, tak obraz prvku  môže nadobúdať tri rôzne hodnoty
môže nadobúdať tri rôzne hodnoty
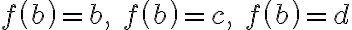
Ak už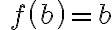 , tak obraz prvku
, tak obraz prvku  môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne
môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne
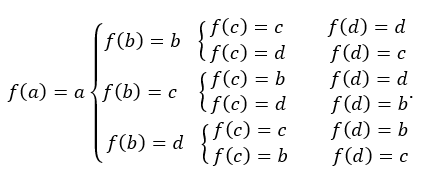
Pre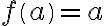 sme dostali permutácie
sme dostali permutácie 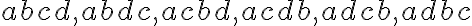 . Podobne budeme postupovať pre
. Podobne budeme postupovať pre 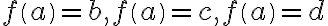 . Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.
. Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.

Na základe postupu použitého v predchádzajúcom príklade môžeme dokázať tvrdenie uvedené vo vete 9, v ktorej je uvedený vzorec pre určenie počtu všetkých permutácii ľubovoľnej množiny .
.
Nájdite všetky permutácie ľubovoľnej štvorprvkovej množiny
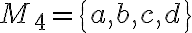 .
.
Riešenie.
Nech
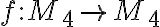 je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
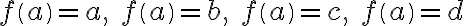 .
.
Ak
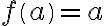 , tak obraz prvku
, tak obraz prvku  môže nadobúdať tri rôzne hodnoty
môže nadobúdať tri rôzne hodnoty
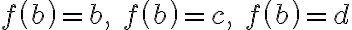
Ak už
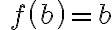 , tak obraz prvku
, tak obraz prvku  môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne
môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne
Pre
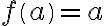 sme dostali permutácie
sme dostali permutácie 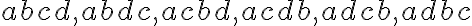 . Podobne budeme postupovať pre
. Podobne budeme postupovať pre 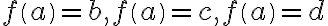 . Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.
. Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.
Na základe postupu použitého v predchádzajúcom príklade môžeme dokázať tvrdenie uvedené vo vete 9, v ktorej je uvedený vzorec pre určenie počtu všetkých permutácii ľubovoľnej množiny
 .
.
Tvrdenie. Pre počet permutácií
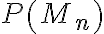 množiny
množiny
 platí vzťah
platí vzťah 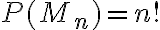
Dôkaz tohto tvrdenia môžeme ľahko urobiť ak využijeme kombinatorické pravidlo súčinu.
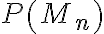 množiny
množiny
 platí vzťah
platí vzťah 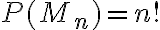
Dôkaz tohto tvrdenia môžeme ľahko urobiť ak využijeme kombinatorické pravidlo súčinu.
