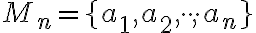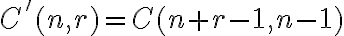Kombinatorika
Partície
Kombinácie s opakovaním
Nech
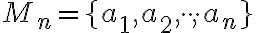 je množina
je množina  kategórií (druhov, prvkov). Vytvorme
kategórií (druhov, prvkov). Vytvorme  -tice z týchto
-tice z týchto
 prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad
prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad 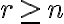 .
.
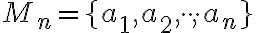 je množina
je množina  kategórií (druhov, prvkov). Vytvorme
kategórií (druhov, prvkov). Vytvorme  -tice z týchto
-tice z týchto
 prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad
prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad 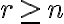 .
.
Definícia.
 -kombinácie s opakovaním definujeme ako
-kombinácie s opakovaním definujeme ako  -tice prvkov z
-tice prvkov z  druhov
druhov 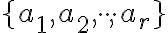 , v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých
, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých  -kombinácií s opakovaním z
-kombinácií s opakovaním z  prvkov budeme označovať symbolom
prvkov budeme označovať symbolom
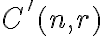 .
.
 -kombinácie s opakovaním definujeme ako
-kombinácie s opakovaním definujeme ako  -tice prvkov z
-tice prvkov z  druhov
druhov 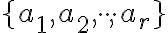 , v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých
, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých  -kombinácií s opakovaním z
-kombinácií s opakovaním z  prvkov budeme označovať symbolom
prvkov budeme označovať symbolom
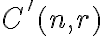 .
.
Príklad
V obchode predávajú tri druhy cukru: kryštálový , práškový
, práškový  a hnedý
a hnedý  v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.
v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.
Riešenie. Uvedieme nejaké možné nákupy, napríklad 2 kilogramový nákup môže byť {1 kg práškového cukru, 1 kg kryštálového cukru}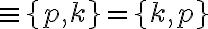 alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru}
alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru} 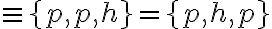 .
.
Všetky nákupy dvoch kilogramov budú predstavovať 2-kombinácie s opakovaním z troch druhov cukru -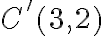 . Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru -
. Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru - 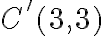 .
.
Pokúste sa vymenovať všetky možné nákupy. Pri nákupe
V obchode predávajú tri druhy cukru: kryštálový
 , práškový
, práškový  a hnedý
a hnedý  v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.
v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.Riešenie. Uvedieme nejaké možné nákupy, napríklad 2 kilogramový nákup môže byť {1 kg práškového cukru, 1 kg kryštálového cukru}
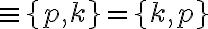 alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru}
alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru} 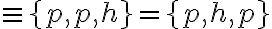 .
.Všetky nákupy dvoch kilogramov budú predstavovať 2-kombinácie s opakovaním z troch druhov cukru -
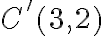 . Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru -
. Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru - 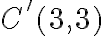 .
.
Pokúste sa vymenovať všetky možné nákupy. Pri nákupe
- dvoch kilogramov máme 6 možností ... vypíšte ich. Otvorte si tabuľu Tu.
- troch kilogramov dostaneme 10 možností... vypíšte ich
Dôkaz.
Nech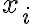 označuje počet výskytu prvku
označuje počet výskytu prvku
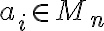 v nejakej
v nejakej  -kombinácií
-kombinácií 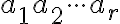 s opakovaním. Potom zrejme musí platiť rovnosť
s opakovaním. Potom zrejme musí platiť rovnosť
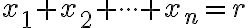 .
.
Napríklad pre nákup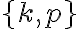 ide o rovnosť
ide o rovnosť 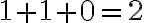
Nech
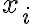 označuje počet výskytu prvku
označuje počet výskytu prvku
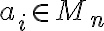 v nejakej
v nejakej  -kombinácií
-kombinácií 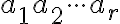 s opakovaním. Potom zrejme musí platiť rovnosť
s opakovaním. Potom zrejme musí platiť rovnosť
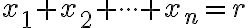 .
.
Napríklad pre nákup
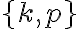 ide o rovnosť
ide o rovnosť 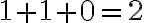
-
Ak k obidvom stranám tejto rovnosti pripočítame číslo
 , tak po menšej úprave dostaneme rovnosť
, tak po menšej úprave dostaneme rovnosť -
Na rovnosť
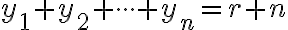 sa môžeme pozerať ako na rozdelenie čísla
sa môžeme pozerať ako na rozdelenie čísla 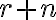 na
na  častí alebo ako na partície (navzájom rôznych aspoň poradím) čísla
častí alebo ako na partície (navzájom rôznych aspoň poradím) čísla 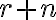 na
na  častí.
častí.
- Počet takýchto partícií je rovný číslu
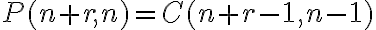 .Tým sme dokázali tvrdenie.
.Tým sme dokázali tvrdenie.
Pre nákup dvoch litrov dostávame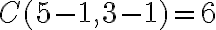 .
.
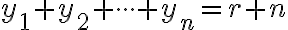 ,
,
kde
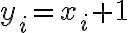 pre
pre 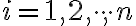 .
.
Pre nákup
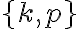 ide o rovnosť
ide o rovnosť 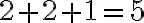 .
Otvorte tabuľu.
.
Otvorte tabuľu.