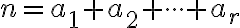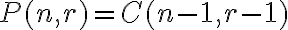Kombinatorika
Partície
Teória partícií predstavuje jednu z najpozoruhodnejších častí klasickej kombinatoriky. V tomto odseku ukážeme len niekoľko zaujímavých výsledkov.
Obyčajne sa pri štúdiu partícií rozlišujú dva prípady. Partície, v ktorých
 pozostávajúcich z presne
pozostávajúcich z presne  sčítancov
sčítancov 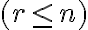 symbolom
symbolom
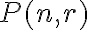 .
.
V ďalšom sa budeme snažiť určiť číslo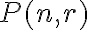 .
.
- záleží na poradí sčítancov
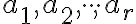 , napríklad partície
, napríklad partície
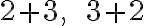 čísla
čísla 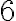 budeme považovať za rôzne
budeme považovať za rôzne
- nezáleží na poradí sčítancov
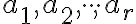 , napríklad partície
, napríklad partície
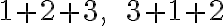 budeme považovať totožné
budeme považovať totožné
 pozostávajúcich z presne
pozostávajúcich z presne  sčítancov
sčítancov 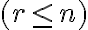 symbolom
symbolom
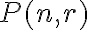 .
.
V ďalšom sa budeme snažiť určiť číslo
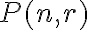 .
.
Nakreslime na priamke vedľa seba  bodov. Medzi nimi máme
bodov. Medzi nimi máme 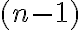 medzier a zvoľme z nich
medzier a zvoľme z nich 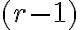 medzier. Táto voľba sa dá zrejme uskutočniť
medzier. Táto voľba sa dá zrejme uskutočniť
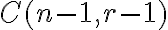
spôsobmi. Vložme do nich zvislé čiarky. Napr.: Rozdeliť číslo 6 na 4 časti znamená zvoliť 3 medzery z 5.

Tým sa pôvodných bodov rozdelí na
bodov rozdelí na  častí, pričom rôznym voľbám
častí, pričom rôznym voľbám 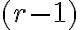 medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla
medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla 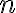 na
na
 častí. Dokázali sme vlastne vetu o počte partícií.
častí. Dokázali sme vlastne vetu o počte partícií.
 bodov. Medzi nimi máme
bodov. Medzi nimi máme 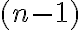 medzier a zvoľme z nich
medzier a zvoľme z nich 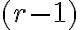 medzier. Táto voľba sa dá zrejme uskutočniť
medzier. Táto voľba sa dá zrejme uskutočniť
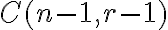
spôsobmi. Vložme do nich zvislé čiarky. Napr.: Rozdeliť číslo 6 na 4 časti znamená zvoliť 3 medzery z 5.

Tým sa pôvodných
 bodov rozdelí na
bodov rozdelí na  častí, pričom rôznym voľbám
častí, pričom rôznym voľbám 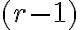 medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla
medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla 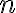 na
na
 častí. Dokázali sme vlastne vetu o počte partícií.
častí. Dokázali sme vlastne vetu o počte partícií.
Príklad. Rozklad čísla 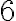 na
na 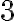 nenulových sčítancov. Vypíšte všetky rozklady.
nenulových sčítancov. Vypíšte všetky rozklady.
Riešenie. Číslo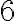 má
má
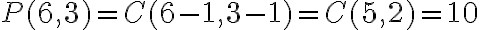 partícií z troch sčítancov. Sú to partície:
partícií z troch sčítancov. Sú to partície:
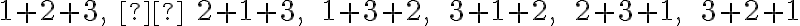
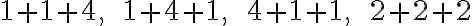 . Otvorte si applet Tu
. Otvorte si applet Tu
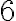 na
na 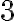 nenulových sčítancov. Vypíšte všetky rozklady.
nenulových sčítancov. Vypíšte všetky rozklady.
Riešenie. Číslo
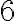 má
má
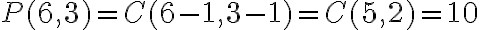 partícií z troch sčítancov. Sú to partície:
partícií z troch sčítancov. Sú to partície:
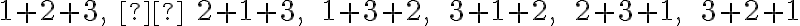
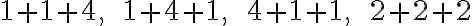 . Otvorte si applet Tu
. Otvorte si applet Tu
Teraz už ľahko určíme počet všetkých rôznych (aspoň) poradím partícií čísla 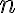 . Ak si to číslo označíme symbolom
. Ak si to číslo označíme symbolom
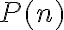 , tak zrejme platí
, tak zrejme platí
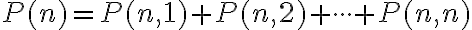 .
.
Použitím vety a identity
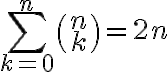
potom dostávame
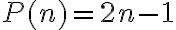 .
.
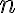 . Ak si to číslo označíme symbolom
. Ak si to číslo označíme symbolom
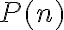 , tak zrejme platí
, tak zrejme platí
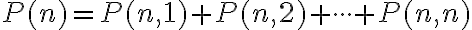 .
.
Použitím vety a identity
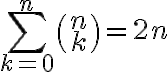
potom dostávame
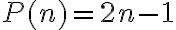 .
.
Partície úzko súvisia s kombináciami s opakovaním. Pokúsme sa vyriešiť nasledujúcu úlohu - nakupovanie v obchode, ktorá predstavuje kombinácie s opakovaním.
Úloha. Koľkými spôsobmi môžeme urobiť nákup, ktorý pozostáva zo 5 litrov mlieka, ak v obchode majú tri druhy mlieka -nízkotučné, polotučné a plnotučné. V nákupe musia byť zastúpené všetky druhy mlieka. Vypíšte všetky možnosti nákupu.
Návod.
Návod.
- Označme si nákup ako usporiadanú trojicu prirodzených čísel
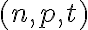 , kde jednotlivé čísla predstavujú koľko litrov sme nakúpili z daného druhu mlieka.
, kde jednotlivé čísla predstavujú koľko litrov sme nakúpili z daného druhu mlieka. - Napríklad trojica
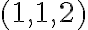 predstavuje nákup 1 litra nízkotučného mlieka a 1 litre polotučného a 2 litre plnotučného mlieka, preto nespĺňa podmienku nákupu.
predstavuje nákup 1 litra nízkotučného mlieka a 1 litre polotučného a 2 litre plnotučného mlieka, preto nespĺňa podmienku nákupu. - Trojica
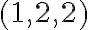 predstavuje nákup 1 litra nízkotučného mlieka a 2 litre polotučného a 2 litre plnotučného mlieka, preto spĺňa podmienku nákupu.
predstavuje nákup 1 litra nízkotučného mlieka a 2 litre polotučného a 2 litre plnotučného mlieka, preto spĺňa podmienku nákupu. - Nákup predstavuje partície, v ktorých záleží na poradí. Vymenovaním všetkých partícií zistíme, že ich je práve 6.
- Vypíšte všetky 6 partície. Otvorte tabuľu Tu.
Tieto podmienky spĺňa zadanie našej úlohy. Sú to teda partície z 5 prvkov a 3 triedy. Pre počet všetkých platí
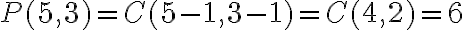 .
.