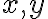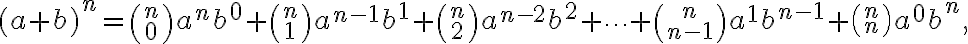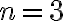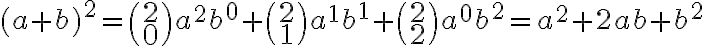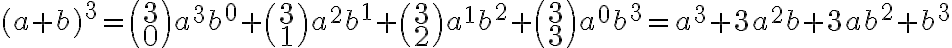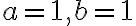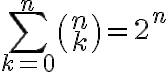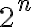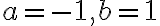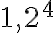Kombinatorika
Binomická veta
Predpokladáme, že študentom sú známe vzorce pre mocniny dvojčlena 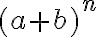 ak
ak 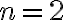 resp. pre
resp. pre 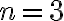 . Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
. Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
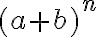 ak
ak 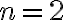 resp. pre
resp. pre 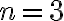 . Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
. Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
Dôkaz vety
Pri dôkaze binomickej vety vychádzame z toho, že v súčine
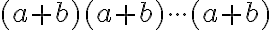
člen
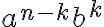
dostaneme tak, že z dvojčlenov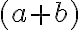 vyberieme
vyberieme 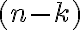 -krát reálne číslo
-krát reálne číslo  a potom
a potom  -krát reálne číslo
-krát reálne číslo  . To je možné práve
. To je možné práve
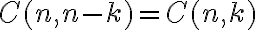
spôsobmi, čím je dôkaz ukončený. Dôkaz binomickej vety môžeme urobiť aj pomocou úplnej matematickej indukcie.
Pri dôkaze binomickej vety vychádzame z toho, že v súčine
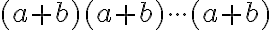
člen
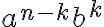
dostaneme tak, že z dvojčlenov
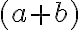 vyberieme
vyberieme 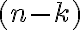 -krát reálne číslo
-krát reálne číslo  a potom
a potom  -krát reálne číslo
-krát reálne číslo  . To je možné práve
. To je možné práve
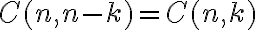
spôsobmi, čím je dôkaz ukončený. Dôkaz binomickej vety môžeme urobiť aj pomocou úplnej matematickej indukcie.
Poznámky