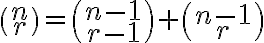Kombinatorika
Kombinácie bez opakovania
Pascalov trojuholník
Pre 1-prvkovú množinu zrejme platí:
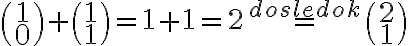
opäť použijeme tvrdenie uvedené v dôsledku teraz pre 2-prvkovú množinu a dostaneme:
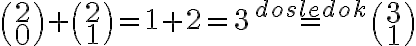
a zároveň pre 2-prvkovú množinu tiež platí:
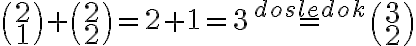 .
.
Takto by sme mohli postupovať pre väčšie hodnoty . Napríklad už poznáme hodnoty
. Napríklad už poznáme hodnoty
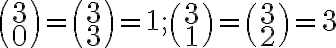
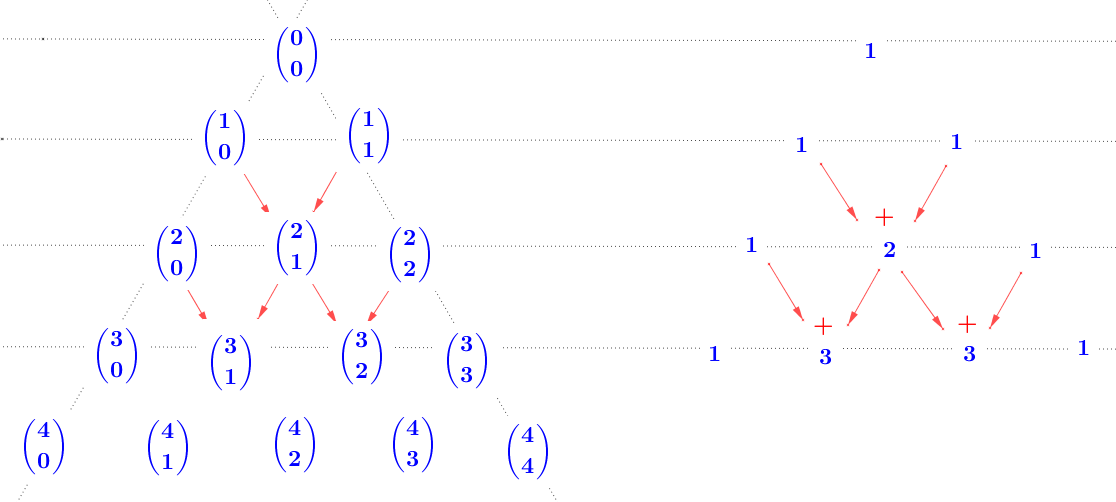
preto ľahko spočítame hodnoty pre . Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.
. Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.
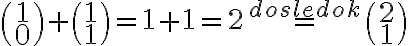
opäť použijeme tvrdenie uvedené v dôsledku teraz pre 2-prvkovú množinu a dostaneme:
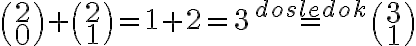
a zároveň pre 2-prvkovú množinu tiež platí:
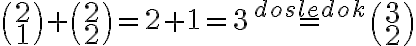 .
.Takto by sme mohli postupovať pre väčšie hodnoty
 . Napríklad už poznáme hodnoty
. Napríklad už poznáme hodnoty
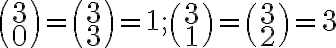
preto ľahko spočítame hodnoty pre
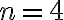 . Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.
. Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.