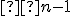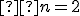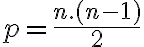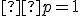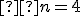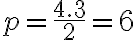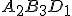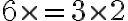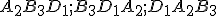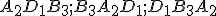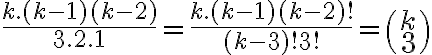Kombinatorika
Kombinácie bez opakovania
Od draka k trojuholníkom
Drak.
Kráľ má osem dcér. Určite, koľkými spôsobmi môže kráľ vybrať dve dcéry, ktoré chce zjesť stohlavý drak. Vzhľadom na to, že drak bude jesť obe princezné naraz, nezáleží na tom (na poradí), ktorú vyberieme ako prvú a ktorú ako druhú.
Kráľ má osem dcér. Určite, koľkými spôsobmi môže kráľ vybrať dve dcéry, ktoré chce zjesť stohlavý drak. Vzhľadom na to, že drak bude jesť obe princezné naraz, nezáleží na tom (na poradí), ktorú vyberieme ako prvú a ktorú ako druhú.
Riešenie.
Postupne vyberáme princezné na raňajky: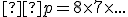 možností. Zrejme nemá cenu rozlišovať výbery typu princezná {Anna, Dana} od {Dana, Anna} resp. kráľov výber {Anna, Dana} je ten istý ako výber {Dana, Anna}. Pozrite si obrázok. Z matematického pohľadu: dvojicu {Anna, Dana} sme započítali dvakrát. Z toho dôvodu počet všetkých možných rôznych kráľových výberov bude rovný číslu
možností. Zrejme nemá cenu rozlišovať výbery typu princezná {Anna, Dana} od {Dana, Anna} resp. kráľov výber {Anna, Dana} je ten istý ako výber {Dana, Anna}. Pozrite si obrázok. Z matematického pohľadu: dvojicu {Anna, Dana} sme započítali dvakrát. Z toho dôvodu počet všetkých možných rôznych kráľových výberov bude rovný číslu 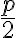 .
.

Princezné A - Anna, B- Barbora, ..., D - Dana, ...
Záver: Každú možnosť sme započítali dvakrát. Preto počet možností ako nakŕmiť draka je polovičná: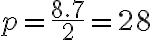 .
.
Postupne vyberáme princezné na raňajky:
- výber: 8 možností
- výber: 7 možností
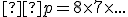 možností. Zrejme nemá cenu rozlišovať výbery typu princezná {Anna, Dana} od {Dana, Anna} resp. kráľov výber {Anna, Dana} je ten istý ako výber {Dana, Anna}. Pozrite si obrázok. Z matematického pohľadu: dvojicu {Anna, Dana} sme započítali dvakrát. Z toho dôvodu počet všetkých možných rôznych kráľových výberov bude rovný číslu
možností. Zrejme nemá cenu rozlišovať výbery typu princezná {Anna, Dana} od {Dana, Anna} resp. kráľov výber {Anna, Dana} je ten istý ako výber {Dana, Anna}. Pozrite si obrázok. Z matematického pohľadu: dvojicu {Anna, Dana} sme započítali dvakrát. Z toho dôvodu počet všetkých možných rôznych kráľových výberov bude rovný číslu 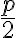 .
.

Princezné A - Anna, B- Barbora, ..., D - Dana, ...
Záver: Každú možnosť sme započítali dvakrát. Preto počet možností ako nakŕmiť draka je polovičná:
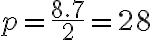 .
.
Analogická a typická úloha pre stredné školy je sformulovaná takto:
Priamky.
V rovine je daných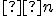 bodov (
bodov ( 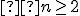 ), z ktorých žiadne tri neležia v jednej priamke. Určite, koľko rôznych priamok je určených týmito bodmi. Odvodený vzťah overte
dosadením konkrétneho čísla miesto
), z ktorých žiadne tri neležia v jednej priamke. Určite, koľko rôznych priamok je určených týmito bodmi. Odvodený vzťah overte
dosadením konkrétneho čísla miesto 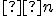 .
.
V rovine je daných
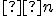 bodov (
bodov ( 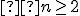 ), z ktorých žiadne tri neležia v jednej priamke. Určite, koľko rôznych priamok je určených týmito bodmi. Odvodený vzťah overte
dosadením konkrétneho čísla miesto
), z ktorých žiadne tri neležia v jednej priamke. Určite, koľko rôznych priamok je určených týmito bodmi. Odvodený vzťah overte
dosadením konkrétneho čísla miesto 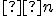 .
.
Riešenie.
Priamka je určená práve dvoma rôznymi bodmi (základná axióma euklidovskej roviny). Budeme hľadať, koľkými spôsobmi je možné vybrať dva rôzne body: Ku každému bodu, ktorý sme vybrali ako prvý, môžeme vystriedať všetky body vybrané ako druhé. Celkový počet takto vybraných priamok je rovný číslu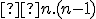 .
Keďže každú možnosť sme započítali dvakrát, počet
.
Keďže každú možnosť sme započítali dvakrát, počet 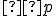 rôznych priamok bude určený vzťahom (vzorcom)
rôznych priamok bude určený vzťahom (vzorcom) 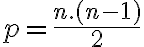 .
.
Priamka je určená práve dvoma rôznymi bodmi (základná axióma euklidovskej roviny). Budeme hľadať, koľkými spôsobmi je možné vybrať dva rôzne body: Ku každému bodu, ktorý sme vybrali ako prvý, môžeme vystriedať všetky body vybrané ako druhé. Celkový počet takto vybraných priamok je rovný číslu
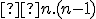 .
Keďže každú možnosť sme započítali dvakrát, počet
.
Keďže každú možnosť sme započítali dvakrát, počet 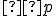 rôznych priamok bude určený vzťahom (vzorcom)
rôznych priamok bude určený vzťahom (vzorcom) 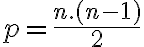 .
.
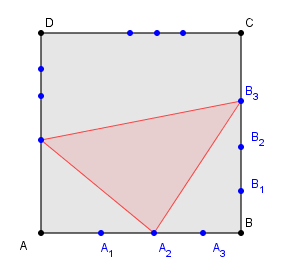
Trojuholníky.
Je daný štvorec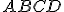 a na každej z jeho strán je daných
a na každej z jeho strán je daných 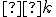 vnútorných bodov. Určite počet trojuholníkov, ktoré majú vrcholy v týchto
bodoch a na rôznych stranách štvorca
vnútorných bodov. Určite počet trojuholníkov, ktoré majú vrcholy v týchto
bodoch a na rôznych stranách štvorca 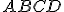 .
.
Je daný štvorec
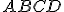 a na každej z jeho strán je daných
a na každej z jeho strán je daných 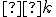 vnútorných bodov. Určite počet trojuholníkov, ktoré majú vrcholy v týchto
bodoch a na rôznych stranách štvorca
vnútorných bodov. Určite počet trojuholníkov, ktoré majú vrcholy v týchto
bodoch a na rôznych stranách štvorca 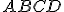 .
.