Uhol a jeho veľkosť, operácie s uhlami
Uhol na ZŠ a SŠ
Seminárne zadania 2
Matematická olympiáda - kategória B, A
-
Nech
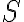 je stred prepony
je stred prepony
 pravouhlého trojuholníka
pravouhlého trojuholníka
 , ktorý nie je rovnoramenný. Označme
, ktorý nie je rovnoramenný. Označme
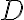 pätu výšky z vrcholu
pätu výšky z vrcholu
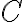 a
a
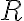 priesečník osi vnútorného uhla pri vrchole
priesečník osi vnútorného uhla pri vrchole
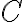 s preponou
s preponou
 . Určte veľkosti vnútorných uhlov tohto trojuholníka, ak platí
. Určte veľkosti vnútorných uhlov tohto trojuholníka, ak platí
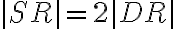 (MO, kat. B, 2014/15).
Riešenie
(MO, kat. B, 2014/15).
Riešenie - Trojuholník
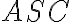 je rovnoramenný (bod
je rovnoramenný (bod
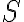 je stredom Tálesovej kružnice opísanej pravouhlému trojuholníku
je stredom Tálesovej kružnice opísanej pravouhlému trojuholníku
 ). Preto uhly
). Preto uhly
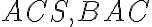 majú rovnakú veľkosť.
majú rovnakú veľkosť.
- Pravouhlé trojuholníky
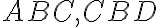 sa zhodujú vo vnútornom uhle pri vrchole
sa zhodujú vo vnútornom uhle pri vrchole
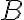 , sú teda podobné. Z toho vyplýva zhodnosť uhlov
, sú teda podobné. Z toho vyplýva zhodnosť uhlov
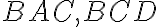 .
.
- Uhly
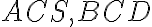 sú teda zhodné a menšie ako
sú teda zhodné a menšie ako
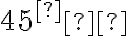 , takže ich do pravého uhla
, takže ich do pravého uhla
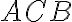 dopĺňa nenulový uhol
dopĺňa nenulový uhol
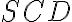 , ktorého os je navyše zhodná s osou celého uhla
, ktorého os je navyše zhodná s osou celého uhla
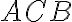 , čo je polpriamka
, čo je polpriamka
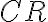 . Zároveň z toho vyplýva aj zhodnosť uhlov
. Zároveň z toho vyplýva aj zhodnosť uhlov
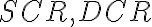 (a tiež to, že bod
(a tiež to, že bod
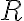 leží medzi bodmi
leží medzi bodmi
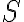 a
a
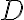 ).
). - Označme
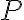 stred úsečky
stred úsečky
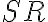 a
a
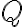 pätu kolmice z bodu
pätu kolmice z bodu
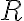 na priamku
na priamku
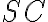 .
. - Pravouhlé trojuholníky
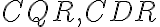 s pravými uhlami pri vrcholoch
s pravými uhlami pri vrcholoch
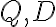 sa zhodujú vo veľkostiach vnútorného uhla pri vrchole
sa zhodujú vo veľkostiach vnútorného uhla pri vrchole
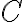 a v dĺžke (spoločnej) prepony
a v dĺžke (spoločnej) prepony
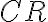 ,sú preto zhodné.
,sú preto zhodné. - Podľa predpokladu úlohy tak platí
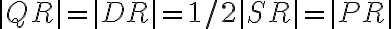 . To znamená, že trojuholník
. To znamená, že trojuholník
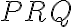 je rovnostranný, takže
je rovnostranný, takže
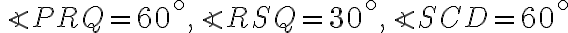 . Keďže uhol pri vrchole
. Keďže uhol pri vrchole
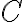 je pravý, vychádza
je pravý, vychádza
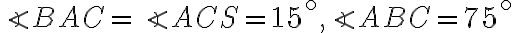
-
Označme
 stred strany
stred strany
 ľubovoľného trojuholníka
ľubovoľného trojuholníka
 . Dokážte, že rovnosť
. Dokážte, že rovnosť
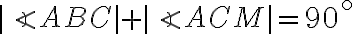 platí práve vtedy, keď je trojuholník
platí práve vtedy, keď je trojuholník
 rovnoramenný so základňou
rovnoramenný so základňou
 alebo pravouhlý s preponou
alebo pravouhlý s preponou
 . (MO, kat. A, školské kolo, 2013/14).
Riešenie
. (MO, kat. A, školské kolo, 2013/14).
Riešenie - Nájdite ďalšie úlohy z MO k téme Uhol a jeho veľkosť, operácie s uhlami.
