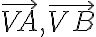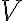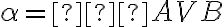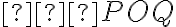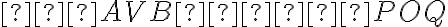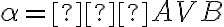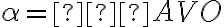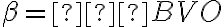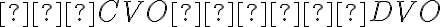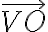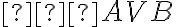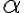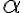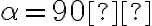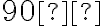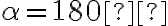Uhol a jeho veľkosť, operácie s uhlami
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Uhol a jeho veľkosť, operácie s uhlami |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | piatok, 3 mája 2024, 21:09 |
Opis
Uhol na ZŠ a SŠ
Základné pojmy
ISCED 2, 6. ročník ZŠ, Tematický celok IV.: Uhol a jeho veľkosť, operácie s uhlami
- Uhol a jeho veľkosť, stupeň (minúta).
- Os uhla a jej konštrukcia. Odhad a meranie veľkosti uhla.
- Priamy, pravý, ostrý a tupý uhol.
Prenášanie a zhodnosť uhlov
Uhol môžeme prenášať pomocou listu papiera alebo pomocou kružidla.
Pohybujte bodom B
Os uhla delí uhol na dva zhodné uhly.
Pohybujte bodom B
Meranie uhlov
- Školský uhlomer sa skladá z pravítka a z polkruhu.
- Na obvode polkruhu je polkružnica, ktorá je rozdelená na 180 rovnakých dielikov.
- Pri polkružnici sú dve číselné stupnice: vonkajšia a vnútorná.
- Vonkajšia stupnica je orientovaná proti smeru hodinových ručičiek, vnútorná v smere hodinových ručičiek.
-

- Polomery
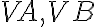 polkružnice určujú navzájom opačné polpriamky
polkružnice určujú navzájom opačné polpriamky
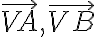 , ktoré reprezentujú priamy uhol.
, ktoré reprezentujú priamy uhol. - Priamy uhol je teda rozdelený na 180 zhodných uhlov so spoločným vrcholom (počiatkom
 polpriamok).
polpriamok). - Každý z nich nazývame stupňom.
- Priamy uhol má veľkosť
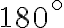 .
.
Jednotkou veľkosti uhla je jeden stupeň, označujeme
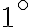 .
.
Menšia jednotka je minúta, zapisujeme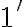 . Jeden stupeň má 60 minút:
. Jeden stupeň má 60 minút:
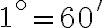 .
.
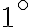 .
.
Menšia jednotka je minúta, zapisujeme
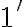 . Jeden stupeň má 60 minút:
. Jeden stupeň má 60 minút:
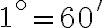 .
.
Uhol na hodinovom ciferníku
Veľkosť uhla, ktoré zvierajú hodinové ručičky.
- Zhodné uhly majú rovnakú veľkosť.
- Základnou jednotkou pre uhol je jeden stupeň.
- Vyskúšajte si odhad pri meraní veľkosti uhlov, ktoré zvierajú hodinové ručičky.
V akom čase bude os hodinovej a os minútovej ručičky zvierať uhol 120°? Nájdite viaceré riešenia.
Uvádzame dve správne odpovede: Napríklad presne pre 4 hod alebo pre 6 hod 54 min 36 sek bude uhol rovný 120°. Pokúste sa vyriešiť úlohu (algebraicky), ktorá je vhodná pre strednú školu.
Na meranie uhlov využívame uhlomer
Applet si stiahnite
Tu
Zemepisná šírka a dĺžka
Základná škola Spojová, 48°44'02.6"N 19°07'17.6"E = 48.734421, 19.121566
• vchod do školy - GPS súradnice: 48°44'03.0"N 19°07'18.0"E; 48.734056, 19.121694

• vchod do školy - GPS súradnice: 48°44'03.0"N 19°07'18.0"E; 48.734056, 19.121694
Zemepisná šírka je uhol
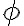 , ktorý zviera rovina rovníka s kolmicou v príslušnom bode na povrchu zemegule.
, ktorý zviera rovina rovníka s kolmicou v príslušnom bode na povrchu zemegule.
Rozlišujeme severnú a južnú zemepisnú šírku. Body rovnakej zemepisnej šírky tvoria kružnicu, ktorú nazývame rovnobežka.
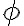 , ktorý zviera rovina rovníka s kolmicou v príslušnom bode na povrchu zemegule.
, ktorý zviera rovina rovníka s kolmicou v príslušnom bode na povrchu zemegule.
Rozlišujeme severnú a južnú zemepisnú šírku. Body rovnakej zemepisnej šírky tvoria kružnicu, ktorú nazývame rovnobežka.
Zemepisná dĺžka je uhol
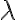 medzi hlavným poludníkom a poludníkom prechádzajúcim cez daný bod.
medzi hlavným poludníkom a poludníkom prechádzajúcim cez daný bod.
Rozlišujeme východnú a západnú zemepisnú dĺžku. Body rovnakej zemepisnej dĺžky tvoria kružnicu, ktorú nazývame poludník.
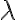 medzi hlavným poludníkom a poludníkom prechádzajúcim cez daný bod.
medzi hlavným poludníkom a poludníkom prechádzajúcim cez daný bod.
Rozlišujeme východnú a západnú zemepisnú dĺžku. Body rovnakej zemepisnej dĺžky tvoria kružnicu, ktorú nazývame poludník.
Vypočítajte vzdialenosť, ktorú predstavujú dve miesta na zemeguli (napr. na rovníku a nultom poludníku), ak ich zemepisná šírka resp. dĺžka sa líši len o
Príklad
- jeden stupeň
- jednu minútu
- jednu sekundu. Pomocou Google Maps nájdite nejaké známe miesta v okolí školy, ktoré majú takéto zemepisné šírky resp. dĺžky.
- Napríklad zadaj GPS súradnice vchodu školy
48°44'02.6"N 19°07'18.0"E a potom pridávaj po 1 sekunde.
Príklad
Kategórie uhlov
Porovnávanie uhlov
Z dvoch uhlov je menší ten, ktorý má menšiu veľkosť
- Uhly sú zhodné práve vtedy, ak majú rovnakú veľkosť.
- Ak uhly nemajú rovnakú veľkosť, tak nie sú zhodné.
Druhy uhlov - rozdelenie podľa veľkosti: ostrý uhol < pravý uhol < tupý uhol < priamy uhol
V literatúre sa uvádzajú aj druhy uhlov, ktoré súvisia s ich veľkosťou:
- Nulový uhol je uhol, ktorého ramená ležia na sebe (všetky ich body sú totožné). Má presne 0°.
- Plný uhol je uhol, ktorého ramená sú totožné (ležia na sebe). Za uhol považujeme celú rovinu okolo nich. Je to doplnok nulového uhla v rovine. Má presne 360°.
- Kosý uhol je uhol, ktorý nie je nulový, pravý, priamy ani plný (šikmý, nepriamy, nerovnobežný).
- Dutý uhol je uhol, ktorý je menší ako priamy.
- Konvexný uhol je uhol priamy, alebo menší než priamy.
- Konkávny uhol je väčší než priamy. Nakreslite takéto druhy uhlov.
Vytvorte applet na meranie uhla, v ktorom sa bude meniť vysvetľujúci text v dôsledku zmeny veľkosti uhla.
Dvojice uhlov
Sú dané dve rovnobežné
priamky
 , ktoré pretína priamka
, ktoré pretína priamka
 v bodoch
v bodoch
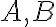 .
.
Uhly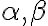 nazývame
súhlasné (obr. vľavo) resp. striedavé (obr. vpravo).
nazývame
súhlasné (obr. vľavo) resp. striedavé (obr. vpravo).
 , ktoré pretína priamka
, ktoré pretína priamka
 v bodoch
v bodoch
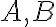 .
.
Uhly
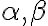 nazývame
súhlasné (obr. vľavo) resp. striedavé (obr. vpravo).
nazývame
súhlasné (obr. vľavo) resp. striedavé (obr. vpravo).
Uhly
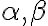 nazývame vrcholové (obr. vľavo) resp. susedné/vedľajšie (obr. vpravo). Pohybuj
bodmi K resp. L.
nazývame vrcholové (obr. vľavo) resp. susedné/vedľajšie (obr. vpravo). Pohybuj
bodmi K resp. L.
Otestuj sa: Interaktívne cvičenia pre SŠ - Dvojice uhlov.
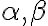 nazývame vrcholové (obr. vľavo) resp. susedné/vedľajšie (obr. vpravo). Pohybuj
bodmi K resp. L.
nazývame vrcholové (obr. vľavo) resp. susedné/vedľajšie (obr. vpravo). Pohybuj
bodmi K resp. L.
Otestuj sa: Interaktívne cvičenia pre SŠ - Dvojice uhlov.
Euklidove Základy - Tvrdenie XIII.
Ak priamka stojí na priamke, vytvára buď dva pravé uhly alebo uhly, ktorých súčet sa rovná dvom pravým uhlom.
Ak priamka stojí na priamke, vytvára buď dva pravé uhly alebo uhly, ktorých súčet sa rovná dvom pravým uhlom.
Dôkaz: (upravený podľa českého prekladu Euklidových Základov)
Nech akákoľvek priamka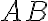 stojaca na priamke
stojaca na priamke
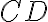 vytvára uhly
vytvára uhly
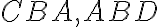 . Hovorím, že buď uhly
. Hovorím, že buď uhly
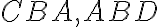 sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
Nech akákoľvek priamka
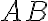 stojaca na priamke
stojaca na priamke
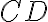 vytvára uhly
vytvára uhly
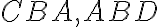 . Hovorím, že buď uhly
. Hovorím, že buď uhly
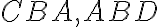 sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
-
Ak sa teraz uhol
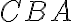 rovná uhlu
rovná uhlu
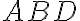 , potom sú to dva pravé uhly.
Def.10
, potom sú to dva pravé uhly.
Def.10
- Ale ak nie, nakreslite
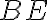 z bodu
z bodu
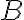 v pravom uhle k
v pravom uhle k
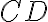 . Preto uhly
. Preto uhly
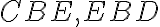 sú dva pravé uhly.
T.11
sú dva pravé uhly.
T.11
- Pretože uhol
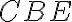 sa rovná súčtu dvoch uhlov
sa rovná súčtu dvoch uhlov
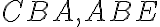 , pridajte uhol
, pridajte uhol
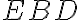 ku každému, takže súčet uhlov
ku každému, takže súčet uhlov
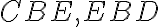 sa rovná súčtu troch uhlov
sa rovná súčtu troch uhlov
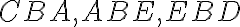 .
Z.2, Z.4
.
Z.2, Z.4
- Pretože uhol
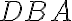 sa rovná súčtu dvoch uhlov
sa rovná súčtu dvoch uhlov
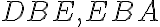 , ku každému z nich pridajte uhol
, ku každému z nich pridajte uhol
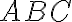 , preto sa súčet uhlov
, preto sa súčet uhlov
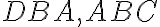 rovná súčtu troch uhlov
rovná súčtu troch uhlov
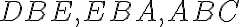 . Z.2, Z.5
. Z.2, Z.5 - Ale súčet uhlov
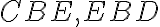 sa tiež ukázal byť rovný súčtu rovnakých troch uhlov a veci, ktoré sa rovnajú rovnakému, sa rovnajú rovnako sebe, preto súčet uhlov
sa tiež ukázal byť rovný súčtu rovnakých troch uhlov a veci, ktoré sa rovnajú rovnakému, sa rovnajú rovnako sebe, preto súčet uhlov
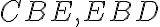 sa rovná súčtu uhlov
sa rovná súčtu uhlov
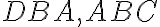 . Uhly ,
. Uhly ,
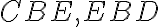 sú však dva pravé uhly, takže súčet uhlov
sú však dva pravé uhly, takže súčet uhlov
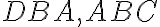 sa tiež rovná dvom pravým uhlom. Z.1, Z.6
sa tiež rovná dvom pravým uhlom. Z.1, Z.6 - Preto ak priama čiara stojí na priamke, vytvára buď dva pravé uhly alebo uhly, ktorých súčet sa rovná dvom pravým uhlom. 1 2 3
Euklidove tvrdenia
Tvrdenie T/XIV
Ak na akejkoľvek priamke a v bode na nej dve priamky na rôznych stranách ležiace tvoria susedné (styčné) uhly dvom pravým rovné, potom tieto priamky sú v priamke medzi sebou.
Ak na akejkoľvek priamke a v bode na nej dve priamky na rôznych stranách ležiace tvoria susedné (styčné) uhly dvom pravým rovné, potom tieto priamky sú v priamke medzi sebou.
Nech na priamke AB a v bode B na nej vytvorte dve priamky BC a BD na rozličných stranách (polrovinách) ležiace a nech súčet susedných uhlov ABC a ABD je rovný dvom pravým uhlom. Hovorím, že BD je v priamej línii s CB.
- Ak BD nie je v priamke s BC, potom vytvorte BE v priamke s CB. ... Post.2
- Pretože priamka AB stojí na priamke CBE, súčet uhlov ABC a ABE sa rovná dvom pravým uhlom. Súčet uhlov ABC a ABD sa tiež rovná dvom pravým uhlom (predpoklad T XIV), preto súčet uhlov CBA a ABE sa rovná súčtu uhlov CBA a ABD. ... T.13, Post.4, Z.1
- Od každého odčítajte uhol CBA. Potom zostávajúci uhol ABE sa rovná zostávajúcemu uhlu ABD, teda menší sa rovná väčšiemu, čo je nemožný. (Spor s podmienkou 1.)
- Preto BE nie je v priamke (v priamej línii) s CB. ... Z.3
- Podobne môžeme dokázať, že okrem BD neexistuje žiadna iná priama čiara.
- Preto ak na akejkoľvek priamke a v bode na nej dve priamky na rôznych ...
- Ak sa teraz uhol CBA rovná uhlu ABD, potom sú to dva pravé uhly. ... Def.10

Nech sa priamky AB a CD pretínajú v bode E. Hovorím, že uhol CEA sa rovná uhlu DEB a uhol BEC sa rovná uhlu AED.
- Pretože priamka AE stojí na priamke CD tvoria uhly CEA a AED, súčet uhlov CEA a AED sa teda rovná dvom pravým uhlom. ... T.13
- Pretože priamka DE stojí opäť na priamke AB, takže uhly AED a DEB sa preto súčet uhlov AED a DEB rovná dvom pravým uhlom.
- Súčet uhlov CEA a AED sa však tiež ukázal ako rovný dvom pravým uhlom, preto sa súčet uhlov CEA a AED rovná súčtu uhlov AED a DEB. ... Post.4
- Od každého odčítajte uhol AED. Potom zostávajúci uhol CEA sa rovná zostávajúcemu uhlu DEB. ... Z1, Z3
- Podobne je možné dokázať, že uhly BEC a AED sú rovnaké.
- Preto, ak sa dve priamky pretínajú, tvoria uhly vrcholové, ktoré sa navzájom rovnajú.

Interpretujte a dokážte Euklidove tvrdenia o uhloch.
Hodiny - uč. pomôcka
V applete môžete nastavovať čas s presnosťou na sekundy
Použitím posuvníkov môžete meniť čas po sekundách. Aktivovaním zaškrtávacích políčok môžete merať uhly a posúvaním bodu "Otáčaj" budete môcť otáčať uhlomerom.
Pracovná verzia Tu
Pracovná verzia Tu
Cvičenie.
Pokúste sa nastaviť hodiny tak, aby hodinová ručička s minútovou ručičkou zvierali presne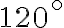 uhol. Nájdite viac (všetky?) riešenia.
uhol. Nájdite viac (všetky?) riešenia.
Pokúste sa nastaviť hodiny tak, aby hodinová ručička s minútovou ručičkou zvierali presne
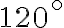 uhol. Nájdite viac (všetky?) riešenia.
uhol. Nájdite viac (všetky?) riešenia.
Poznámky.
Hodiny - applet
Postup konštrukcie si stiahnete Tu
Základné etapy tejto konštrukcie popisujeme v nasledujúcich troch bodoch
Applet .
- Zostrojíme "základ" hodín:
- Stred hodinového ciferníka nazveme Stred, do vstupného poľa zadáme:
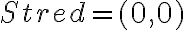
- Vytvoríme bod s názvom
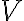 so súradnicami
so súradnicami
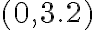
- Body pri 12 hodine
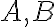 pre konce hodinovej a minútovej ručičky, do vstupného poľa zadáme:
pre konce hodinovej a minútovej ručičky, do vstupného poľa zadáme:
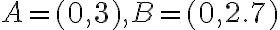
- Kružnice na ciferníku pre zobrazovanie minút a hodín, napr. do vstupného poľa zadajte
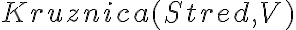
- Na minútovom ciferníku (kružnici) vytvoríme zoznam modrých bodov:
vo vstupnom poli zadáme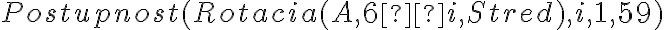 alebo použijeme príkaz "Vytvoriť zoznam", ktorý nájdeme v rozbaľovanej ikonke "Uhol"
alebo použijeme príkaz "Vytvoriť zoznam", ktorý nájdeme v rozbaľovanej ikonke "Uhol" - Upravíme body, ktoré budú predstavovať celé "hodiny", napr. červenou farbou.
-
Navrhneme číselné hodnoty pre hodiny, minúty, sekundy pomocou posuvníkov
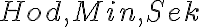 ako aj číslo
ako aj číslo
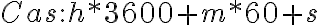
- Definujeme odpovedajúce uhly a rotácie pre hodiny, minúty, sekundy. Napríklad
- Pre uhol, ktorý bude zvierať sekundová ručička s polpriamkou (Stred, A) zadáme do vstupného poľa
\
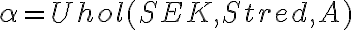 \)
\)
- Pre koncový bod sekundovej ručičky zadáme
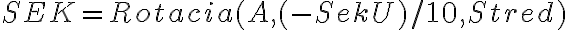
- Zostrojíme ručičky: pomocnú kružnicu v strede a k nej dotyčnice, ...
- Ručičky sa skladajú z kruhového výseku, ktorý je ohraničený bodmi dotyku a trojuholníkom
Seminárne zadanie 1
Vytvorte si podkapitolu s názvom "Euklidove Základy" v knihe "Moja 1. kniha", v ktorej budú prezentované niektoré dôkazy Euklidových tvrdení o uhloch, trojuholníkoch, ...
• Ukážka/applet tvrdenia T16 .
• Pozrite si prepisy niektorých Euklidových tvrdení Texty tvrdení
• Ukážka/applet tvrdenia T16 .
• Pozrite si prepisy niektorých Euklidových tvrdení Texty tvrdení
Matematická olympiáda kategória Z
-
Prokop zostrojil trojuholník
 , ktorého vnútorný uhol pri vrchole
, ktorého vnútorný uhol pri vrchole
 bol väčší ako
bol väčší ako
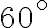 a vnútorný uhol pri vrchole
a vnútorný uhol pri vrchole
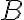 bol menší ako
bol menší ako
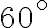 . Juraj narysoval v polrovine určenej priamkou
. Juraj narysoval v polrovine určenej priamkou
 a bodom
a bodom
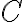 bod
bod
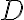 , a to tak, že trojuholník
, a to tak, že trojuholník
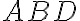 bol rovnostranný. Potom chlapci zistili, že trojuholníky
bol rovnostranný. Potom chlapci zistili, že trojuholníky
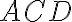 a
a
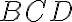 sú rovnoramenné s hlavným vrcholom
sú rovnoramenné s hlavným vrcholom
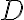 . Určte veľkosť uhla
. Určte veľkosť uhla
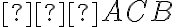 .(MO, kat. Z7, 2017/18)
.(MO, kat. Z7, 2017/18)
Nápad. Nájdite vzťahy medzi vnútornými uhlami uvedených trojuholníkov. Riešenie
- Veľkosti vnútorných uhlov v trojuholníku
 označíme postupne
označíme postupne
 .
. - V rovnostrannom trojuholníku
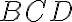 majú všetky vnútorné uhly veľkosť
majú všetky vnútorné uhly veľkosť
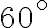 .
. - Zhodné uhly pri základni rovnoramenného trojuholníka
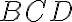 majú veľkosť
majú veľkosť
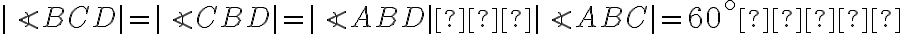 .
. - Zhodné uhly pri základni rovnoramenného trojuholníka
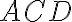 majú veľkosť
majú veľkosť
 .
. - Veľkosť neznámeho uhla
 môžeme vyjadriť ako
môžeme vyjadriť ako
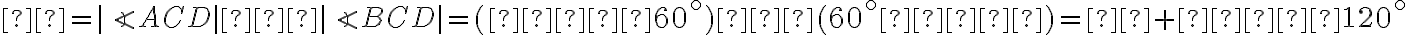 .
. - Súčet veľkostí vnútorných uhlov v trojuholníku
 je
je
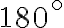 , teda
, teda
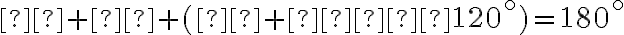 , z čoho vyplýva
, z čoho vyplýva
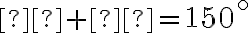 .
. - Uhol
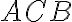 má veľkosť
má veľkosť
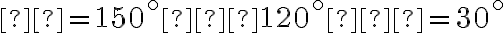 .
.
- Veľkosti vnútorných uhlov v trojuholníku
- V ostrouhlom trojuholníku
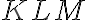 má uhol
má uhol
 veľkosť
veľkosť
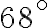 . Bod
. Bod
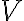 je priesečníkom výšok a
je priesečníkom výšok a
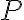 je pätou výšky na stranu
je pätou výšky na stranu
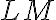 . Os uhla
. Os uhla
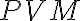 je rovnobežná so stranou
je rovnobežná so stranou
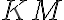 . Porovnajte veľkosti uhlov
. Porovnajte veľkosti uhlov
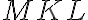 a
a
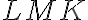 . (MO, kat. Z8, 2017/18)
. (MO, kat. Z8, 2017/18)
Nápad. Uvažujte os súmernosti uhla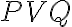 .
Riešenie
.
Riešenie - Os uhla
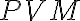 je kolmá na os uhla
je kolmá na os uhla
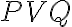 - sú to osi vrcholových uhlov.
- sú to osi vrcholových uhlov. - Keďže os uhla
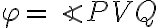 je zároveň kolmá na rovnobežku
je zároveň kolmá na rovnobežku
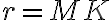 , tak je zároveň výškou v trojuholníku
, tak je zároveň výškou v trojuholníku
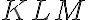 .
.
- Trojuholník
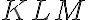 musí byť rovnoramenný s hlavným vrcholom
musí byť rovnoramenný s hlavným vrcholom
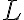 .
. - Uhly pri základni
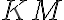 majú rovnakú veľkosť
majú rovnakú veľkosť
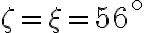 .
.
Ak v trojuholníku
 os uhla
os uhla
 je rovnobežná so stranou
je rovnobežná so stranou
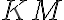 , tak trojuhoník
, tak trojuhoník
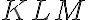 je rovnoramenný.
je rovnoramenný.
Seminárne zadania 2
Matematická olympiáda - kategória B, A
-
Nech
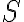 je stred prepony
je stred prepony
 pravouhlého trojuholníka
pravouhlého trojuholníka
 , ktorý nie je rovnoramenný. Označme
, ktorý nie je rovnoramenný. Označme
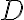 pätu výšky z vrcholu
pätu výšky z vrcholu
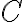 a
a
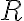 priesečník osi vnútorného uhla pri vrchole
priesečník osi vnútorného uhla pri vrchole
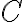 s preponou
s preponou
 . Určte veľkosti vnútorných uhlov tohto trojuholníka, ak platí
. Určte veľkosti vnútorných uhlov tohto trojuholníka, ak platí
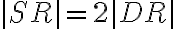 (MO, kat. B, 2014/15).
Riešenie
(MO, kat. B, 2014/15).
Riešenie - Trojuholník
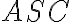 je rovnoramenný (bod
je rovnoramenný (bod
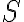 je stredom Tálesovej kružnice opísanej pravouhlému trojuholníku
je stredom Tálesovej kružnice opísanej pravouhlému trojuholníku
 ). Preto uhly
). Preto uhly
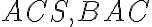 majú rovnakú veľkosť.
majú rovnakú veľkosť.
- Pravouhlé trojuholníky
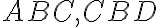 sa zhodujú vo vnútornom uhle pri vrchole
sa zhodujú vo vnútornom uhle pri vrchole
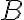 , sú teda podobné. Z toho vyplýva zhodnosť uhlov
, sú teda podobné. Z toho vyplýva zhodnosť uhlov
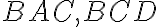 .
.
- Uhly
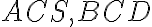 sú teda zhodné a menšie ako
sú teda zhodné a menšie ako
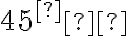 , takže ich do pravého uhla
, takže ich do pravého uhla
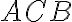 dopĺňa nenulový uhol
dopĺňa nenulový uhol
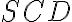 , ktorého os je navyše zhodná s osou celého uhla
, ktorého os je navyše zhodná s osou celého uhla
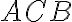 , čo je polpriamka
, čo je polpriamka
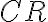 . Zároveň z toho vyplýva aj zhodnosť uhlov
. Zároveň z toho vyplýva aj zhodnosť uhlov
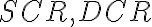 (a tiež to, že bod
(a tiež to, že bod
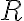 leží medzi bodmi
leží medzi bodmi
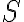 a
a
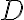 ).
). - Označme
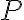 stred úsečky
stred úsečky
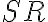 a
a
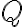 pätu kolmice z bodu
pätu kolmice z bodu
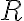 na priamku
na priamku
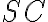 .
. - Pravouhlé trojuholníky
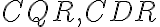 s pravými uhlami pri vrcholoch
s pravými uhlami pri vrcholoch
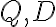 sa zhodujú vo veľkostiach vnútorného uhla pri vrchole
sa zhodujú vo veľkostiach vnútorného uhla pri vrchole
 a v dĺžke (spoločnej) prepony
a v dĺžke (spoločnej) prepony
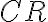 ,sú preto zhodné.
,sú preto zhodné. - Podľa predpokladu úlohy tak platí
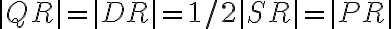 . To znamená, že trojuholník
. To znamená, že trojuholník
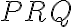 je rovnostranný, takže
je rovnostranný, takže
 . Keďže uhol pri vrchole
. Keďže uhol pri vrchole
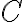 je pravý, vychádza
je pravý, vychádza
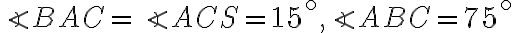
-
Označme
 stred strany
stred strany
 ľubovoľného trojuholníka
ľubovoľného trojuholníka
 . Dokážte, že rovnosť
. Dokážte, že rovnosť
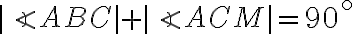 platí práve vtedy, keď je trojuholník
platí práve vtedy, keď je trojuholník
 rovnoramenný so základňou
rovnoramenný so základňou
 alebo pravouhlý s preponou
alebo pravouhlý s preponou
 . (MO, kat. A, školské kolo, 2013/14).
Riešenie
. (MO, kat. A, školské kolo, 2013/14).
Riešenie - Nájdite ďalšie úlohy z MO k téme Uhol a jeho veľkosť, operácie s uhlami.