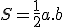Interaktívna geometria - planimetria (pracovná verzia)
Historické poznámky
Slovo geometria pochádza z gréckeho výrazu hé gé meteón, čo znamená vymeriavanie pozemkov pomocou lán. Pozri prácu [SED]. Matematika ako veda vznikla v Grécku približne v období 6. - 5. st. pred n. l.
Základy geometrie nachádzame už v Babylone, Egypte, Indii a Číne. Veľký rozmach zaznamenala grécka matematika. K zásadnému pokroku v rozvoji
geometrie prispeli významní grécki matematici Thales, Pytagoras a Euklides.
Euklidove Základy môžeme považovať za základy planimetrie, stereometrie a geometrickej algebry. Uvedieme ukážku riešenia úlohy o výpočte obsahu rovnoramenného trojuholníka z obdobia mezopotámskej ríše. Pripomíname, že matematika tohto obdobia používala šesťdesiatkovú číselnú sústavu.
Úloha. (Babylon)
Je daný trojuholník so stranami: (1,40) dĺžka každej z dvoch strán, (2,20) šírka. Aká je plocha?
Je daný trojuholník so stranami: (1,40) dĺžka každej z dvoch strán, (2,20) šírka. Aká je plocha?
Obsah trojuholníka v Babylone podľa starobabylonskej tabuľky
YBC 8633, na ktorej je klinovým písmom vyrytý postup riešenia úlohy na výpočet obsahu rovnoramenného trojuholníka.
Poznámky
Na výpočet obsahov trojuholníkov používali mezopotámski matematici nasledovné vzorce:
Na výpočet obsahov trojuholníkov používali mezopotámski matematici nasledovné vzorce:
K rozvoju geometrie prispeli aj egytskí účenci, ktorí boli nútení po každoročných záplavách Nílu nanovo rozmeriavať pozemkové parcely. Zároveň museli ovládať aj postupy pri rozdeľovaní úrody. Z toho vznikla potreba vedieť vypočítať obsahy rôznych geometrických útvarov ako aj postupy riešenia jednoduchých rovníc. Pozrite si ukážky:
Egypt - obdobie elementárnych matematických pojmov.
Rhindov a Moskovský papyrus.
Výpočet obsahov obdĺžnikov, kruhov, trojuholníkov a objemy kvádrov, zrezaných kužeľov a pyramíd. Riešenie rovníc - pozrite si riešenie úlohy R40 z Rhindovho papyrusu.
Egypt - obdobie elementárnych matematických pojmov.
Rhindov a Moskovský papyrus.
Výpočet obsahov obdĺžnikov, kruhov, trojuholníkov a objemy kvádrov, zrezaných kužeľov a pyramíd. Riešenie rovníc - pozrite si riešenie úlohy R40 z Rhindovho papyrusu.
Úloha
Je treba rozdeliť 100 chlebov medzi 5 mužov tak, aby bola jedna sedmina z troch horných pre dvoch mužov dole.
Je treba rozdeliť 100 chlebov medzi 5 mužov tak, aby bola jedna sedmina z troch horných pre dvoch mužov dole.
Poznámky k pôvodnému riešeniu, ktorý je uvedený na papyruse. Pozrite tiež prácu [BEC, 2003]
Podmienku, že jedna sedmina z troch horných pre dvoch mužov dole, môžeme vyjadriť vzťahom:
![\small 1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)] \small 1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)]](https://lms.umb.sk/filter/tex/pix.php/075067788dc5db2c973e66c5c78bbde5.png)
Z predchádzajúceho vzťahu vypočítame
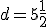
Ide teda o postupnosť
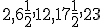 ,
,
ktorej súčet je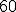 . Číslo
. Číslo 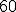 musíme vynásobiť číslom
musíme vynásobiť číslom
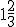 ,
,
aby sme získali požadovaný súčet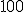 . Týmto číslom musíme preto vynásobiť aj členy vyššie uvedenej postupnosti.
Hľadaná aritmetická postupnosť je teda:
. Týmto číslom musíme preto vynásobiť aj členy vyššie uvedenej postupnosti.
Hľadaná aritmetická postupnosť je teda:
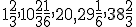 ,
,
ktorej diferencia je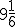 . Tento výsledok však na papyruse nie je uvedený.
. Tento výsledok však na papyruse nie je uvedený.
- Celkový počet chlebov je 100 a je potrebné tieto chleby nejakým spôsobom rozdeliť medzi 5 mužov. V úlohe sa spomínajú traja horní muži a dvaja dolní. Toto naznačuje určité usporiadanie, ale nie je celkom isté, že ide o aritmetickú postupnosť. To vyplýva až z prezentovaného riešenia.
- Ďalej je tu podmienka, ktorú je možné interpretovať tak, že súčet počtu chlebov troch horných mužov v usporiadaní sa rovná súčtu chlebov dvoch mužov dole v usporiadaní.
Podmienku, že jedna sedmina z troch horných pre dvoch mužov dole, môžeme vyjadriť vzťahom:
![\small 1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)] \small 1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)]](https://lms.umb.sk/filter/tex/pix.php/075067788dc5db2c973e66c5c78bbde5.png)
Z predchádzajúceho vzťahu vypočítame
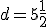
Ide teda o postupnosť
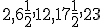 ,
,
ktorej súčet je
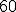 . Číslo
. Číslo 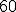 musíme vynásobiť číslom
musíme vynásobiť číslom
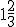 ,
,
aby sme získali požadovaný súčet
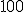 . Týmto číslom musíme preto vynásobiť aj členy vyššie uvedenej postupnosti.
Hľadaná aritmetická postupnosť je teda:
. Týmto číslom musíme preto vynásobiť aj členy vyššie uvedenej postupnosti.
Hľadaná aritmetická postupnosť je teda:
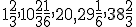 ,
,
ktorej diferencia je
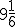 . Tento výsledok však na papyruse nie je uvedený.
. Tento výsledok však na papyruse nie je uvedený.
V súčasnosti by sa tento príklad mohol počítať takto:
Chybný predpoklad by sme nahradili neznámou a dostali by sme dve rovnice o dvoch neznámych:
a dostali by sme dve rovnice o dvoch neznámych:
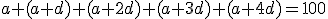
![\small a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )] \small a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )]](https://lms.umb.sk/filter/tex/pix.php/791d47ac4a45210eaeb4efc1098ece19.png) .
.
po ekvivalentných úpravách by sme dospeli k tomu istému výsledku.
Chybný predpoklad by sme nahradili neznámou
 a dostali by sme dve rovnice o dvoch neznámych:
a dostali by sme dve rovnice o dvoch neznámych:
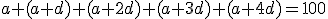
![\small a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )] \small a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )]](https://lms.umb.sk/filter/tex/pix.php/791d47ac4a45210eaeb4efc1098ece19.png) .
.
po ekvivalentných úpravách by sme dospeli k tomu istému výsledku.
Matematika ako veda vznikla v Grécku približne v období 6. - 5. st. pred n. l. Gréci ako prví prestali riešiť iba otázku ako, ale hľadali aj
odpovede na otázku prečo. Významní predstavitelia gréckej matematiky: Tháles, Pytagoras, Euklides

Elementy (zdroj:http://en.wikipedia.org); Kniha II, Návrh 5 - pozrite Tu.
Otvorte si applet Tu. (Aktivujte si navigačný panel.)
V starom Grécku
- Bol vytvorený systém základných vzťahov (axióm) a požiadaviek (postulátov) - Euklidove Základy. Takýto kompletne spracovaný systém bol publikovaný v Euklidových Základoch. Pozrite si práce [EUC] a [SER]. Toto dielo sa považuje za základy planimetrie, stereometrie a geometrickej algebry. Existuje český preklad od Servíta Tu, Heathov preklad je v online verzi od D.E.Joyce Tu. V roku 2022 vyšiel v nakladateľstve Perfekt slovenský preklad s komentármi od profesora J. Čižmára.
- Grécki matematici začali matematické tvrdenia dokazovať , pričom používali deduktívnu metódu. Pokúšali sa vyriešiť aj tri preslávené problémy
- trisekcia uhla (rozdelenie uhla na tri rovnaké uhly)
- zdvojenie kocky (nájdenie kocky, ktorej objem sa rovná dvojnásobku kocky pôvodnej)
- kvadratúru kruhu (nájdenie štvorca, ktorý má rovnaký obsah ako daný kruh),